Fundquellen für kostenloses Material zur Didaktik der Mathematik
Auf dieser Seite findet ihr mehr als 370 Lesezeichen / Linktipps zu thematisch sortierten Webseiten mit Gratis - Unterrichtsmaterial zur Mathematik. Dazu Hinweise auf interaktive Selbstlern-Webseiten, Webseiten mit kostenfreien Arbeitsblättern, Kopiervorlagen, Vorlagen und Generatoren für Übungsblätter, Karopapier + Lineaturen. Darüber hinaus Webseiten zum Mathematik - Fachwortschatz für den DaF/DaZ-Unterricht, Infos zu Dyskalkulie + Rechenschwäche und Differenzierungsmaterial.Frohes und erfolgreiches Stöbern und Unterrichten!
Hinweis: Schlagworte mit einem ➜ führen zu einer anderen Teilseite meiner Website
Linktipp an Freunde
per Mail versenden: 🖂
Link defekt? Linktipps? ➥ Mail an Autenrieths.de
Aufgabensammlungen, Materialien und Arbeitsblätter
Kopiervorlagen, Mathe-Lexika, Didaktisches Material + Anleitungen➜ Abschnitt ansehen / wegblenden
➜ siehe auch
Linktipps zu Arbeitsblattsammlungen
➜ siehe auch Beispielaufgaben für VERA 3 und VERA 8
➜ siehe auch Blogs mit Unterrichtsbeispielen (v.a. Grundschule)
➜ siehe auch Beispielaufgaben für VERA 3 und VERA 8
➜ siehe auch Blogs mit Unterrichtsbeispielen (v.a. Grundschule)
Digitalisierte Lehrwerke zum Download
❱25Q2❱ ➜ archive-org-search-Mathematik+LehrbuchDigitalisierte Mathematik-Lehrbücher auf archive.org
❱25Q2❱ ➜ archive-org-search-Mathematik+Schulbuch
Digitalisierte Mathematik-Schulbücher auf archive.org
❱25Q2❱ ➜ archive-org-search-Mathematik+Aufgaben
Digitalisierte Mathematik-Schulbücher auf archive.org
❱25Q2❱ ➜ archive-org-search-Mathematikunterricht
Digitalisierte Bücher zum Mathematikunterricht auf archive.org
❱25Q2❱ ➜ archive-org-search-VorlesungenUberGeschichteDerMathematikIi
Moritz Cantor: Vorlesungen über die Geschichte der Mathematik, 1892
❱25Q2❱ ➜ mathematikalpha-de-mathematikschulbuecher
Digitalisierte 'Mathematikbücher von Friedrich Barth
❱21Q3❱ ➜ mathematikalpha-de-mathematikschulbuecher
Digitalisierte 'alte' Mathematikbücher von der Nachkriegszeit bis 1989 - dem Mauerfall. Es sind 120 Bücher verfügbar, davon 72 als Abschrift
❱24Q3❱ ➜ mathematikalpha-de-schuelerbuecherei
Hier sind 138 LaTex-Abschriften von Mathematiklehrwerken abgelegt. Alle Bücher können im PDF-Format einzeln oder vollständig als ZIP-Datei aufgerufen werden.
Sammlungen von Arbeitsblättern und Aufgaben zur Mathematik online
❱24Q4❱ ➜ brinkmann-du.de/Oberstufenmathematik + Sek I, Berufsgrundschuljahr + Abiturvorbereitung, Aufgaben, Formeln und Tabellen
❱24Q4❱ ➜ archive.org: fjls-49.0
Matheaufgaben / Material für Klassen 1-13
❱24Q4❱ ➜ archive.org: fjls-148.0
Mathelexikon und Pythagoras- Unterrichtsinhalte der Klasse 5-8
❱24Q4❱ ➜ interaktiv-lernen-net-id=13&Itemid=108
Arbeitsblätter für 5.-8.Jahrgangsstufe. Zahlensystem, Dezimalbrüche, Bruchrechnen, Ganze Zahlen, Grundrechenarten, Tabellen zum Eintragen von Flächenmaßen / Längenmaßen
❱24Q4❱ ➜ internet4classrooms-com-printables
Hunderte Arbeitsblätter für alle möglichen Themen und Jahrgänge in Mathematik.
❱21❱ ➜ archive-org-ne-lo-net2-de-selbstlernmaterial
Eine riesige Aufgabensammlung, auch interaktives Selbstlernmaterial für Mathematik und Physik für Vera 8 und Abschlussprüfungen (4800 Aufgaben) für SEK I und SEK II (EUKLID DynaGeo)(längere Ladezeit, da aus archive-org eingebunden). Es ist möglich, dass manche Links nicht mehr funktionieren.
❱24Q4❱ ➜ mathe-online
Eine Galerie multimedialer Lernhilfen (incl. Lexikon), Puzzles online erstellen u.a.
❱23Q2❱ ➜ Einige Tausend Aufgaben der Mathematik-Olympiaden
Die Datei der Aufgaben und Lösungen zur Mathematik-Olympiade enthält jetzt 4695 Aufgaben der Klassenstufen 1 bis 12 Dazu die DDR-Mathematik-Abiturprüfungsaufgaben von 1953 bis 1990 mit Lösungen, Zentrale Aufgabenstellungen und Abschlussprüfungen der Klassen 6 bis 9 (DDR) u.v.a.m.
❱24Q4❱ ➜ matheraum
Offene Informations- und Vorhilfegemeinschaft, die den Zugang zur Mathematik erleichtern will mit Wiki und Materialsammlung
❱24Q4❱ ➜ mathematische-basteleien
Für Gymnasium: Faltanleitungen, Puzzles, Zahlenspielereien, Arbeitsanleitungen
❱24Q4❱ ➜ matheschmidt
Bastelbögen für Platonische Körper und Materialien für den Matheunterricht Klasse 5-12
❱22Q4❱ ➜ archive-org-oesi-mediennutzung
Mehr als 300 Unterrichtsentwürfe und Lehrproben. Manche Verknüpfungen führen jedoch ins Nirvana bei Lycos. Klasse 1-4, Mathe, Deutsch, Sachunterricht, Kunst -(längere Ladezeit, da aus archive-org eingebunden)
❱24Q4❱ ➜ referendar-de-forum-Matheübungszirkel
Wie funktioniert ein Matheübungszirkel? Tipps von Referendaren
❱24Q4❱ ➜ reitberger-berlin
Didaktisches Material selbst herstellen (Klasse 1-6) Tipps und Anleitungen
❱24Q4❱ ➜ schlauistwow.de/
Unterrichts- und Übungsmaterial für die Klassen 3-13
❱24Q4❱ ➜ tb-u-de-boerse-s_ma1-html
Tauschbörse Unterricht - hunderte Arbeitsblätter
❱24Q4❱ ➜ web.archive-uni-flensburg-mathe-zero
Zero - Mathematik online (Uni Flensburg) - Darstellungen der Geometrie usw.
❱24Q4❱ ➜ walter-fendt
Texte, Applets, Links zum Mathematikunterricht, Physik und Astronomie
❱24Q4❱ ➜ walter-fendt-de-m14d
Java-Applets zur Mathematik
❱24Q4❱ ➜ wilfriedmetze-html-eingang
Stolperwörtertest, Arbeitsblätter, Übungsblätter für die 1.Klasse (Addition)
❱24Q4❱ ➜ wissenschafts=Mathematik
In der Zeitschrift Bild der Wissenschaft findet man die Mathematik bei den Naturwissenschaften und dort interessante Artikel
❱24Q4❱ ➜ unterrichten-zum-de-Mathe-mit-Mieze-Mia
Verschiedene Übungsblätter zur Zahleneinführung, Grundrechenarten usw für Grundschule
❱21❱ ➜ zum-de-mathematik-digital
Die Linkdatenbank von Mathematikdigital.de ist nach Klassenstufen und Lehrplanthemen geordnet. Damit soll zu jedem Thema des Lehrplans eine Art „Best of“-Liste von Materialien im Internet zur Verfügung stehen.
❱24Q4❱ ➜ zebis-ch-unterricht-mathematik
Suchergebnis "Mathematik" am Schweizerischen Bildungsserver
❱24Q4❱ ➜ dwu-unterrichtsmaterialien-de
Sammlung kostenloser Unterrichtsmaterialien zum Unterricht in den Fächern Physik und Mathematik der Sekundarstufe bis ca. Klasse 10 momentan 706 Medien zu 330 Themen
❱24Q4❱ ➜ zum-de-Faecher-M-SELECTM
Unterrichtsmaterialien zum Fach Mathe auf dem Server des ZUM. TOP!
❱24Q4❱ ➜ zum-de-Faecher-freiarb-klaptest
Klapptests (Übungsblätter) zu Grundrechenarten, Bruchrechnen, Zahlsysteme, Flächenberechnungen Römischen Zahlen, Volumen, Zins downloadbare Arbeitsblätter
Arbeitsblattgeneratoren Mathematik
Online-Arbeitsblattgeneratoren, Excel-Tabellen zur Arbeitsblatterstellung➜ Abschnitt ansehen / wegblenden
➜ siehe auch
Arbeitsblattgeneratoren für alle Fächer
❱24Q4❱➜ siehe auch
autenrieths-haupt-mathe-addition-subtraktion-test
Excel-Tabelle Addition/Subtraktion als Arbeitsblatt - Wird die Tabelle aktualisiert, entsteht durch die Zufallsfunktion ein neues Arbeitsblatt Damit die Tabelle bearbeitet werden kann, diese auf den eigenen Rechner abspeichern!
❱24Q4❱➜ siehe auch autenrieths-haupt-mathe-Grundrechenuebungen2-xls
Excel-Tabelle Addition/Subtraktion/Multiplikation/Division als Arbeitsblatt - Wird die Tabelle aktualisiert, entsteht durch die Zufallsfunktion ein neues Arbeitsblatt. Oben links steht auf Arbeitsblatt und Lösungsblatt jeweils eine Kennziffer, damit die Blätter einander zugeordnet werden können Damit die Tabelle bearbeitet werden kann, diese auf den eigenen Rechner abspeichern!
❱24Q4❱ ➜ chip-de-downloads-Rechenblatt-Generator_69771166
Kostenloser Arbeitsblattgenerator für Grundrechenaufgaben
❱24Q4❱ ➜ sikore-schiffner-tischer
Sicheres Kopfrechnen - Online-Arbeitsblattgenerator für Kettenaufgaben
❱24Q4❱ ➜ senteacher-print-mathematics
Arbeitsblattgenerator: Polygone, Münzmemory, Uhren, Monate (engl), Additionsaufgaben uvam.
❱24Q4❱ ➜ theofel-magic-magquad
Magische Quadrate online erstellen
❱24Q4❱ ➜ worksheeps-aufgaben
Hier können Arbeitsblätter automatisch erstellt werden, von einfachen Grundrechenaufgaben bis zur Kurvendiskussion.
Excel-Tabelle Addition/Subtraktion als Arbeitsblatt - Wird die Tabelle aktualisiert, entsteht durch die Zufallsfunktion ein neues Arbeitsblatt Damit die Tabelle bearbeitet werden kann, diese auf den eigenen Rechner abspeichern!
❱24Q4❱➜ siehe auch autenrieths-haupt-mathe-Grundrechenuebungen2-xls
Excel-Tabelle Addition/Subtraktion/Multiplikation/Division als Arbeitsblatt - Wird die Tabelle aktualisiert, entsteht durch die Zufallsfunktion ein neues Arbeitsblatt. Oben links steht auf Arbeitsblatt und Lösungsblatt jeweils eine Kennziffer, damit die Blätter einander zugeordnet werden können Damit die Tabelle bearbeitet werden kann, diese auf den eigenen Rechner abspeichern!
❱24Q4❱ ➜ chip-de-downloads-Rechenblatt-Generator_69771166
Kostenloser Arbeitsblattgenerator für Grundrechenaufgaben
❱24Q4❱ ➜ sikore-schiffner-tischer
Sicheres Kopfrechnen - Online-Arbeitsblattgenerator für Kettenaufgaben
❱24Q4❱ ➜ senteacher-print-mathematics
Arbeitsblattgenerator: Polygone, Münzmemory, Uhren, Monate (engl), Additionsaufgaben uvam.
❱24Q4❱ ➜ theofel-magic-magquad
Magische Quadrate online erstellen
❱24Q4❱ ➜ worksheeps-aufgaben
Hier können Arbeitsblätter automatisch erstellt werden, von einfachen Grundrechenaufgaben bis zur Kurvendiskussion.
Linktipps + Materialkisten
➜ Abschnitt ansehen / wegblenden
❱23Q2❱ ➜
bildungsserver-berlin-brandenburg-de-imint-grundschule-themenkisten
Themenkisten mit Materialien zum Download für die Grundschule. Themen: Brüche, Längen, Gewichte, Gleichungen, Längen, Masse, Würfel, Zeit, Tiere und Mathematik, Kombinatorik, Muster und Strukturen
❱24Q4❱ ➜ arndt-bruenner-de/mathe/mathekurse
Umfangreiche Materialsammlung im Bereich Mathe
❱24Q4❱ ➜ educ-ethz-ch-unterrichtsmaterialien-mathematik
Unterrichtsmaterialien Mathematik vom EducETH - ETH-Kompetenzzentrum für Lehren und Lernen (Eidgenossenschaftliche Technische Hochschule Zürich))
❱24Q4❱ ➜ hirnwindungen-de-Unterricht-index
Links zu Arbeitsblatt-Seiten Mathe
❱24Q4❱ ➜ mathe-werkstatt-de-web-links
Die Linksammlung der Mathe-Werkstatt. Eher gymnasial, aber sehr umfangreich!
❱24Q4❱ ➜ mathematik-olympiaden-de-aufgaben
Offzielle Aufgabenblätter der vergangenen Mathematik-Olympiaden
❱24Q4❱ ➜ mathematikunterricht-de-sitemap
Ka's Materialkiste und Linksammlung - teilweise veraltet?
❱24Q4❱ ➜ mathewelt
Die Linksammlung der Mathe-Welt. Unterrichtsmaterialien Klasse 11, Übungsblätter
❱24Q4❱ ➜ nrich-maths-org
(e)NRICH(ment)- Mathematik mit Suchmaschine von der mathematischen Fakultät der Uni Cambridge
❱24Q4❱ ➜ matheprojekt-ph-tirol
Projekt Mathematische Bildung: Mathematik bereichern - Miteinander bewegen - Mehr bewirken
❱24Q4❱ ➜ zum-de-Faecher-M-mathematik-digital/index.php
Materialien zu Unterrichtsthemen Klasse 5 bis 13, sortiert
❱24Q4❱ ➜ unterrichten-zum-de-wiki-Mathematik
Materialien nach Unterrichtsthemen und Klassenstufen sortiert
Themenkisten mit Materialien zum Download für die Grundschule. Themen: Brüche, Längen, Gewichte, Gleichungen, Längen, Masse, Würfel, Zeit, Tiere und Mathematik, Kombinatorik, Muster und Strukturen
❱24Q4❱ ➜ arndt-bruenner-de/mathe/mathekurse
Umfangreiche Materialsammlung im Bereich Mathe
❱24Q4❱ ➜ educ-ethz-ch-unterrichtsmaterialien-mathematik
Unterrichtsmaterialien Mathematik vom EducETH - ETH-Kompetenzzentrum für Lehren und Lernen (Eidgenossenschaftliche Technische Hochschule Zürich))
❱24Q4❱ ➜ hirnwindungen-de-Unterricht-index
Links zu Arbeitsblatt-Seiten Mathe
❱24Q4❱ ➜ mathe-werkstatt-de-web-links
Die Linksammlung der Mathe-Werkstatt. Eher gymnasial, aber sehr umfangreich!
❱24Q4❱ ➜ mathematik-olympiaden-de-aufgaben
Offzielle Aufgabenblätter der vergangenen Mathematik-Olympiaden
❱24Q4❱ ➜ mathematikunterricht-de-sitemap
Ka's Materialkiste und Linksammlung - teilweise veraltet?
❱24Q4❱ ➜ mathewelt
Die Linksammlung der Mathe-Welt. Unterrichtsmaterialien Klasse 11, Übungsblätter
❱24Q4❱ ➜ nrich-maths-org
(e)NRICH(ment)- Mathematik mit Suchmaschine von der mathematischen Fakultät der Uni Cambridge
❱24Q4❱ ➜ matheprojekt-ph-tirol
Projekt Mathematische Bildung: Mathematik bereichern - Miteinander bewegen - Mehr bewirken
❱24Q4❱ ➜ zum-de-Faecher-M-mathematik-digital/index.php
Materialien zu Unterrichtsthemen Klasse 5 bis 13, sortiert
❱24Q4❱ ➜ unterrichten-zum-de-wiki-Mathematik
Materialien nach Unterrichtsthemen und Klassenstufen sortiert
Mathematikunterricht Sek I/II/Berufsschule
Unterrichtsmaterial für höhere Klassen➜ Abschnitt ansehen / wegblenden
➜ siehe auch
Materialien für den Mathematikunterricht an Fö, GHS und RS, sowie Infos zu Dyskalkulie
➜ siehe auch Projektideen für Unterricht und Schulfest
➜ siehe auch Faszinierende Mathematik
➜ siehe auch (Interaktive) Übungsaufgaben für die HS-/RS-Abschlussprüfung
➜ siehe auch Projektideen für Unterricht und Schulfest
➜ siehe auch Faszinierende Mathematik
➜ siehe auch (Interaktive) Übungsaufgaben für die HS-/RS-Abschlussprüfung
❱21❱ ➜
123mathe-de-mathe-gesamtuebersicht
Aufgaben aus vielen Themenbereichen mit Ergebnissen für Berufsgrundschuljahr und Oberstufe
❱21❱ ➜ 123mathe-de
Arbeitsblätter und Materialien für das Berufsgrundbildungsjahr - auch für Klasse 9 verwendbar
❱21❱ ➜ arndt-bruenner.de/mathe/index/indexframe
Die Mathematik-Seiten von Arndt Brünner. Umfangreich und fundiert
❱21❱ ➜ bildungsserver-de-db-fachlist-fach=3056
Liste von Online-Ressourcen für den Mathematik-Untericht. mehrere hundert Quellen!
❱21❱ ➜ blume-programm-de-ab-boerse-index-htm
Die Arbeitsblattsammlung von Bob Blume
❱21❱ ➜ brinkmann-du.de/
Oberstufenmathematik + Sek I, Berufsgrundschuljahr + Abiturvorbereitung, Aufgaben, Formeln und Tabellen
❱21❱ ➜ start-drothler-net-mathematik
Mathe Sek I Klasse 5 - Oberstufe + Abitur. Interaktive Übungsaufgaben
❱21❱ ➜ educ.ethz-ch-unterrichtsmaterialien-mathematik-html
Aufgaben für SEK I bis Abitur der ETH Zürich
❱21❱ ➜ fersch.de/
Interaktive Formelsammlungen + PDF-Bücher zur Mathematik
❱21❱ ➜ geogebra-org-cms
GeoGebra ist eine kostenlose und plattforumunabhängige dynamische Mathematik Software für Schulen, die Geometrie, Algebra und Analysis verbindet. Das Java-Programm läuft ohne Installation online. - evtl. wird noch eine Java-Runtime installiert. GeoGebra hat bereits mehrere internationale Preise gewonnen, darunter der europäische und deutsche Bildungssoftware Preis
❱21❱ ➜ gfs.khmeyberg.de/Klassenarbeiten-Klausuren/Mathematik-Klausuren-Klassenarbeiten
Klassenarbeiten und Klausuren von Klasse 5-13 (Gym) - mit Lösungen!
❱21❱ ➜ matheguru.com/uebungen-aufgaben
über 100 Übungen aus den Bereichen Algebra, Geometrie, Stochastik (Statistik und Wahrscheinlichkeitsrechnung), Analysis und lineare Algebra von einfacher Bruchrechnung bis hin zu Hochschulstatistik.
❱21❱ ➜ mathekurs.ch/
Mathe für Gymnasium Oberstufe
❱21❱ ➜ mathematik.ch
Anwendungen und Unterrichtshilfen der Mathematik, gymnasial: Puzzles (Rätsel),'Spiele', Euromillions, Swisslotto, Geschichte, Mathematiker, Zitate, Maturaprüfungen, Witze (+IQ-Test), Links
❱21❱ ➜ mathematikphysik
Zahlreiche Arbeitsblätter und Tutorials für Klasse 5-13 Realschule und Gym
❱21❱ ➜ mathewelt.de/start
REHs MatheWelt bietet Unterrichtshilfen für Mathematiklehrerinnen und Mathematiklehrer in der gymnasialen Oberstufe. Diese Seite ist nicht nur für Lehrer interessant, denn hier erhaltet ihr viele Arbeitsblätter zum lernen.Vielleicht finden sich ja gleiche Aufgaben in der nachsten Klassenarbeit... Daneben werden noch einige interessanten Links zur Mathematik genannt
❱21Q3❱ ➜ mathportal-org
Free calculators, formulas & lessons. Solve for free all your math problems in one place.
❱21Q3❱ ➜ mathgoodies-com-lessons-list
FREE Step by Step Math Lessons. Our math lessons are designed to make math meaningful to the student. Each math lesson provides in-depth instruction ideal for learners of all ages and abilities.
❱21❱ ➜ raschweb.de/
Mathe und Physikaufgaben von Klasse 5 - 12
❱21❱ ➜ roro-seiten.de/
Mathematik Abiturvorbereitung, Rechenfertigkeiten, Übungen, Arbeitsblatter
❱21❱ ➜ schule-bw-de-faecher-und-schularten-mathematisch-naturwissenschaftliche-faecher-mathematik
Materialien und Links im Mathematik-Fachportal vom Landesbildungsserver Baden-Württemberg
❱21❱ ➜ stbit.de/
Kompaktlehrbücher zur Mathematik und Physik (ebooks), Aufgaben Mathematik und Physik g8 - Skripte und Aufgaben Physik g9
❱21❱ ➜ strobl-f.de/uebmath.html
Grundwissen und Übungsaufgaben Mathematik. Die 10 wichtigsten Grundwissens-Themen jeder Jahrgangsstufe stehen hier auf jeweils einer Seite bereit
❱21❱ ➜ madincea.hier-im-netz.de
Materialien für den Matheunterricht, Klasse 7-11
❱21❱ ➜ tb-u-de-boerse-s_ma1-html
Tauschbörse Unterricht - hunderte Arbeitsblätter
❱24Q2❱ ➜ archive-org-mathe.tu-freiberg.de/inst/theomath/schlinks/ (längere Ladezeit, da aus archive-org eingebunden)
Umfangreiche Linksammlung zu Mathe und Physik - Stand 2020
❱21❱ ➜ smart.uni-bayreuth
Aufgabensammlung zur Mathematik, nach Jahrgangsstufen sortiert. für Gym und Realschule
❱21❱ ➜ walter-fendt
Texte, Applets, Links zu Mathematik, Physik und Astronomie
❱21❱ ➜ walter-fendt-math-htm
Java-Applets zur Mathematik
❱21❱ ➜ de-wikiversity-org-wiki-Mathematik
Wikiversity-Lernplattform, Fachbereich_Mathematik (Ableger der der Wikipedia)
Wikiversity ist eine Plattform zum gemeinschaftlichen Lernen, Lehren, Nachdenken und Forschen. In Kursen wird Wissen didaktisch aufbereitet und abgerufen. Kolloquien dienen dem fachlichen Gedankenaustausch. In Projekten kann neuen Fragestellungen nachgegangen werden. Durch die Entwicklung und Bereitstellung freier Kurs- und Lernmaterialien soll der ungehinderte Zugang zum Wissen verbessert werden
❱21❱ ➜ dwu-unterrichtsmaterialien-de-umamtg
Unterrichtsmaterialiensammlung von Kollege Dieter Welz - umfangreichst !
Aufgaben aus vielen Themenbereichen mit Ergebnissen für Berufsgrundschuljahr und Oberstufe
❱21❱ ➜ 123mathe-de
Arbeitsblätter und Materialien für das Berufsgrundbildungsjahr - auch für Klasse 9 verwendbar
❱21❱ ➜ arndt-bruenner.de/mathe/index/indexframe
Die Mathematik-Seiten von Arndt Brünner. Umfangreich und fundiert
❱21❱ ➜ bildungsserver-de-db-fachlist-fach=3056
Liste von Online-Ressourcen für den Mathematik-Untericht. mehrere hundert Quellen!
❱21❱ ➜ blume-programm-de-ab-boerse-index-htm
Die Arbeitsblattsammlung von Bob Blume
❱21❱ ➜ brinkmann-du.de/
Oberstufenmathematik + Sek I, Berufsgrundschuljahr + Abiturvorbereitung, Aufgaben, Formeln und Tabellen
❱21❱ ➜ start-drothler-net-mathematik
Mathe Sek I Klasse 5 - Oberstufe + Abitur. Interaktive Übungsaufgaben
❱21❱ ➜ educ.ethz-ch-unterrichtsmaterialien-mathematik-html
Aufgaben für SEK I bis Abitur der ETH Zürich
❱21❱ ➜ fersch.de/
Interaktive Formelsammlungen + PDF-Bücher zur Mathematik
❱21❱ ➜ geogebra-org-cms
GeoGebra ist eine kostenlose und plattforumunabhängige dynamische Mathematik Software für Schulen, die Geometrie, Algebra und Analysis verbindet. Das Java-Programm läuft ohne Installation online. - evtl. wird noch eine Java-Runtime installiert. GeoGebra hat bereits mehrere internationale Preise gewonnen, darunter der europäische und deutsche Bildungssoftware Preis
❱21❱ ➜ gfs.khmeyberg.de/Klassenarbeiten-Klausuren/Mathematik-Klausuren-Klassenarbeiten
Klassenarbeiten und Klausuren von Klasse 5-13 (Gym) - mit Lösungen!
❱21❱ ➜ matheguru.com/uebungen-aufgaben
über 100 Übungen aus den Bereichen Algebra, Geometrie, Stochastik (Statistik und Wahrscheinlichkeitsrechnung), Analysis und lineare Algebra von einfacher Bruchrechnung bis hin zu Hochschulstatistik.
❱21❱ ➜ mathekurs.ch/
Mathe für Gymnasium Oberstufe
❱21❱ ➜ mathematik.ch
Anwendungen und Unterrichtshilfen der Mathematik, gymnasial: Puzzles (Rätsel),'Spiele', Euromillions, Swisslotto, Geschichte, Mathematiker, Zitate, Maturaprüfungen, Witze (+IQ-Test), Links
❱21❱ ➜ mathematikphysik
Zahlreiche Arbeitsblätter und Tutorials für Klasse 5-13 Realschule und Gym
❱21❱ ➜ mathewelt.de/start
REHs MatheWelt bietet Unterrichtshilfen für Mathematiklehrerinnen und Mathematiklehrer in der gymnasialen Oberstufe. Diese Seite ist nicht nur für Lehrer interessant, denn hier erhaltet ihr viele Arbeitsblätter zum lernen.Vielleicht finden sich ja gleiche Aufgaben in der nachsten Klassenarbeit... Daneben werden noch einige interessanten Links zur Mathematik genannt
❱21Q3❱ ➜ mathportal-org
Free calculators, formulas & lessons. Solve for free all your math problems in one place.
❱21Q3❱ ➜ mathgoodies-com-lessons-list
FREE Step by Step Math Lessons. Our math lessons are designed to make math meaningful to the student. Each math lesson provides in-depth instruction ideal for learners of all ages and abilities.
❱21❱ ➜ raschweb.de/
Mathe und Physikaufgaben von Klasse 5 - 12
❱21❱ ➜ roro-seiten.de/
Mathematik Abiturvorbereitung, Rechenfertigkeiten, Übungen, Arbeitsblatter
❱21❱ ➜ schule-bw-de-faecher-und-schularten-mathematisch-naturwissenschaftliche-faecher-mathematik
Materialien und Links im Mathematik-Fachportal vom Landesbildungsserver Baden-Württemberg
❱21❱ ➜ stbit.de/
Kompaktlehrbücher zur Mathematik und Physik (ebooks), Aufgaben Mathematik und Physik g8 - Skripte und Aufgaben Physik g9
❱21❱ ➜ strobl-f.de/uebmath.html
Grundwissen und Übungsaufgaben Mathematik. Die 10 wichtigsten Grundwissens-Themen jeder Jahrgangsstufe stehen hier auf jeweils einer Seite bereit
❱21❱ ➜ madincea.hier-im-netz.de
Materialien für den Matheunterricht, Klasse 7-11
❱21❱ ➜ tb-u-de-boerse-s_ma1-html
Tauschbörse Unterricht - hunderte Arbeitsblätter
❱24Q2❱ ➜ archive-org-mathe.tu-freiberg.de/inst/theomath/schlinks/ (längere Ladezeit, da aus archive-org eingebunden)
Umfangreiche Linksammlung zu Mathe und Physik - Stand 2020
❱21❱ ➜ smart.uni-bayreuth
Aufgabensammlung zur Mathematik, nach Jahrgangsstufen sortiert. für Gym und Realschule
❱21❱ ➜ walter-fendt
Texte, Applets, Links zu Mathematik, Physik und Astronomie
❱21❱ ➜ walter-fendt-math-htm
Java-Applets zur Mathematik
❱21❱ ➜ de-wikiversity-org-wiki-Mathematik
Wikiversity-Lernplattform, Fachbereich_Mathematik (Ableger der der Wikipedia)
Wikiversity ist eine Plattform zum gemeinschaftlichen Lernen, Lehren, Nachdenken und Forschen. In Kursen wird Wissen didaktisch aufbereitet und abgerufen. Kolloquien dienen dem fachlichen Gedankenaustausch. In Projekten kann neuen Fragestellungen nachgegangen werden. Durch die Entwicklung und Bereitstellung freier Kurs- und Lernmaterialien soll der ungehinderte Zugang zum Wissen verbessert werden
❱21❱ ➜ dwu-unterrichtsmaterialien-de-umamtg
Unterrichtsmaterialiensammlung von Kollege Dieter Welz - umfangreichst !
Symbole, Lineaturen, Clipart, Grafiken
Karopapier / Millimeterpapier selbst drucken➜ Abschnitt ansehen / wegblenden
❱24Q4❱ ➜
edupic-math_gr
Mathematische Symbole, Bruchdarstellungen, Uhren ...
❱24Q4❱ ➜ spot.fho-emden-messtech-gpaper
Programm (.exe-Datei) zum Drucken von Diagrammpapier - genial! Karopapier, Isometrische Linien, Musiknotenpapier... zahllose (veränderbare) Variationen
❱24Q4❱ ➜ mar-braun-patente-karopap
Karopapier
❱24Q4❱ ➜ millimeterpapier
Wie der Name sagt: Hier kann man sich Milimeterpapier ausdrucken lassen
❱24Q4❱ ➜ papersnake-grundschule
Lineaturen für die Grundschule
❱24Q4❱ ➜ Photoscape
Mit diesem freien Bild- und Fotobearbeitungsprogramm können auch verschiedenste Lineaturen erstellt werden, u.a. Karos, Notenlinien, Schreiblinien... genial!
❱23Q2❱ ➜ papier-schulkreis-de-karopapier
Lineatur-Papier, Zahlenstrahl-Vorlagen, Millimeterpapier, Musik-Notenlinien, Logarithmenpapier (Logarithmuspapier), Karopapier, Koordinatensystem-Vorlagen, Stundenplan-Vorlagen, Würfelnetze zum Basteln, Quadernetze, Etiketten, Maßband 190cm und Lineale, Punktraster-Vordrucke
❱24Q4❱ ➜ unterrichtsmaterial-schule.-unterrichtsmaterialm
Rechenkaros
Mathematische Symbole, Bruchdarstellungen, Uhren ...
❱24Q4❱ ➜ spot.fho-emden-messtech-gpaper
Programm (.exe-Datei) zum Drucken von Diagrammpapier - genial! Karopapier, Isometrische Linien, Musiknotenpapier... zahllose (veränderbare) Variationen
❱24Q4❱ ➜ mar-braun-patente-karopap
Karopapier
❱24Q4❱ ➜ millimeterpapier
Wie der Name sagt: Hier kann man sich Milimeterpapier ausdrucken lassen
❱24Q4❱ ➜ papersnake-grundschule
Lineaturen für die Grundschule
❱24Q4❱ ➜ Photoscape
Mit diesem freien Bild- und Fotobearbeitungsprogramm können auch verschiedenste Lineaturen erstellt werden, u.a. Karos, Notenlinien, Schreiblinien... genial!
❱23Q2❱ ➜ papier-schulkreis-de-karopapier
Lineatur-Papier, Zahlenstrahl-Vorlagen, Millimeterpapier, Musik-Notenlinien, Logarithmenpapier (Logarithmuspapier), Karopapier, Koordinatensystem-Vorlagen, Stundenplan-Vorlagen, Würfelnetze zum Basteln, Quadernetze, Etiketten, Maßband 190cm und Lineale, Punktraster-Vordrucke
❱24Q4❱ ➜ unterrichtsmaterial-schule.-unterrichtsmaterialm
Rechenkaros
Grundrechenarten, Fach- und Grundwortschatz
Grundbegriffe international / Fachtermini in den Herkunftsprachen➜ Abschnitt ansehen / wegblenden
➜ siehe auch
Rechenfehler / Dyskalkulie- weiter unten
➜ siehe auch schulbibo-de-daz-in-faechern-fachwortschatz-mathe
Auf meiner DAF-DAZ-Seite findet ihr auch Hinweise zu Rechenverfahren in den Herkunftsländern der Geflohenen, Vertriebenen und Migranten sowie einen Fachwortschatz Mathematik in Herkunftssprachen sowie Materialien
Vorbemerkung:
"Sprachbildung im Fachunterricht – warum?"
In diesem Handout werden Konzepte und Begründungen, sowie Stolpersteine für die Lernenden genannt. Ein Paper von Marika Schwaiger, M.A. (Universität Hamburg), 2012
❱22Q1❱ ➜ web-archive-org-li-hamburg-download-pdf-sprachfoerderung-in-jedem-fach
Sprachbildung in jedem Fach: Sprechen, Lesen und Schreiben lernen - Erfolgreiche Konzepte der Sprachförderung. 38 Folien (längere Ladezeit, da aus archive-org eingebunden)
➜ siehe auch schulbibo-de-daz-in-faechern-fachwortschatz-mathe
Auf meiner DAF-DAZ-Seite findet ihr auch Hinweise zu Rechenverfahren in den Herkunftsländern der Geflohenen, Vertriebenen und Migranten sowie einen Fachwortschatz Mathematik in Herkunftssprachen sowie Materialien
Vorbemerkung:
"Sprachbildung im Fachunterricht – warum?"
In diesem Handout werden Konzepte und Begründungen, sowie Stolpersteine für die Lernenden genannt. Ein Paper von Marika Schwaiger, M.A. (Universität Hamburg), 2012
❱22Q1❱ ➜ web-archive-org-li-hamburg-download-pdf-sprachfoerderung-in-jedem-fach
Sprachbildung in jedem Fach: Sprechen, Lesen und Schreiben lernen - Erfolgreiche Konzepte der Sprachförderung. 38 Folien (längere Ladezeit, da aus archive-org eingebunden)
❱24Q4❱ ➜
deutsch4alle-jimdoweb-com-matech-mathematik
Mathematik für Flüchtlinge - Hier finden Sie Materialien zur Mathematik sprachsensibel ausgearbeitet
❱24Q4❱ ➜ kira.dzlm-material
Kira: "Kinder rechnen anders." Mathe - mehr als Ausrechnen befasst sich schwerpunktmäßig mit den prozessbezogenen Kompetenzen des Mathematikunterrichts (Problemlösen/kreativ sein, Argumentieren, Modellieren und Darstellen/Kommunizieren
❱24Q3❱ ➜ mathematikalpha-de-fachwoerterbuch
Fachwörterlisten für Mathematik: Fremdsprache → Deutsch: Bulgarisch (6000 Begriffe, 59 Seiten) // Dänisch (9000 Begriffe, 93 Seiten) // Englisch (14000 Begriffe, 143 Seiten) // Esperanto (10000 Begriffe, 94 Seiten) // Finnisch (7000 Begriffe, 78 Seiten) // Französisch (14000 Begriffe, 157 Seiten) // Griechisch (6000 Begriffe, 61 Seiten) // Hebräisch (5700 Begriffe, 49 Seiten) // Isländisch (9000 Begriffe, 86 Seiten) // Italienisch (14000 Begriffe, 155 Seiten) // Kroatisch (6000 Begriffe, 53 Seiten) // Latein (5900 Begriffe, 52 Seiten) // Niederländisch (9000 Begriffe, 97 Seiten) // Polnisch (11000 Begriffe, 110 Seiten) // Portugiesisch (8000 Begriffe, 82 Seiten) // Rumänisch (6000 Begriffe, 56 Seiten) // Russisch (19000 Begriffe, 211 Seiten) // Schwedisch (9000 Begriffe, 93 Seiten) // Serbisch (5900 Begriffe, 59 Seiten) // Slowenisch (6000 Begriffe, 65 Seiten) // Spanisch (8000 Begriffe, 86 Seiten) // Tschechisch (10000 Begriffe, 94 Seiten) // Türkisch (6000 Begriffe, 60 Seiten) // Ungarisch (6000 Begriffe, 70 Seiten) // Vietnamesisch (8000 Begriffe, 77 Seiten)
Fachwörterlisten für Mathematik: Deutsch → Fremdsprache: Bulgarisch (61 Seiten) // Dänisch (94 Seiten) // Englisch (144 Seiten) // Esperanto (99 Seiten) // Finnisch (78 Seiten) // Deutsch-Französisch (157 Seiten) // Griechisch (64 Seiten) // Hebräisch (49 Seiten) // Isländisch (87 Seiten) // Italienisch (156 Seiten) // Deutsch-Kroatisch (55 Seiten) // Latein (53 Seiten) // Niederländisch (97 Seiten) // Polnisch (116 Seiten) // Portugiesisch (83 Seiten) // Deutsch-Rumänisch (59 Seiten) // Russisch (219 Seiten) // Schwedisch (94 Seiten) // Serbisch (62 Seiten) // Slowenisch (68 Seiten) // Deutsch-Spanisch (86 Seiten) // Tschechisch (98 Seiten) // Türkisch (63 Seiten) // Ungarisch (73 Seiten) // Vietnamesisch (80 Seiten)
❱24Q4❱ ➜ mediator-programme
Förderprogramme: Norbert Römer stellt eigene Mediator-Übungsprogramme für den Erstrechenunterricht zum Download bereit
❱24Q4❱ ➜ mathewortschatz.schule
Interaktiver Wortschatztrainer für mathematische Fachbegriffe - deutsch, türkisch-slowenisch-kroatisch-englisch-tschechisch-ungarisch mit Fachwortlisten Mathematik zu den einzelnen Sprachen als PDF-Dateien
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe_wortschatz
Mathe-Wortschatz mit Abbildungen Bild deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_de
Mathe-Wortschatz alphabetisch deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_tu
Mathewortschatz Deutsch-Türkisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_tu_d
Mathewortschatz Türkisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_slo
Mathewortschatz Deutsch-Slowakisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_slo_d
Mathewortschatz Slowakisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_kr
Mathewortschatz Deutsch-Kroatisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_kr_d
Mathewortschatz Kroatisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_en
Mathewortschatz Deutsch-Englisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_en_d
Mathewortschatz Englisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_cz
Mathewortschatz Deutsch-Tschechisch
❱24Q4❱ ➜ mathewortschatz.schule.at/woerterbuecher/mathe.wortschatz_cz_d
Mathewortschatz Tschechisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_hu
Mathewortschatz Deutsch-Ungarisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_hu_d
Mathewortschatz Ungarisch-Deutsch
❱22Q1❱ ➜ uni-due-prodaz-seiteneinsteiger
Übersicht schriftlicher Rechenverfahren verschiedener Herkunftsländer
Daraus folgende Verweise auf detaillierte Darstellungen:
Matheknüller: Rechnen wie die alten Inder - Vedische Mathematik, eine (fast) vergessene Wissenschaft - und mehr
❱22Q1❱ ➜ de-wikipedia-org-Vedische-Mathematik-Rechenmethoden
Vedische Rechenverfahren in der Wikipedia
Mathematik für Flüchtlinge - Hier finden Sie Materialien zur Mathematik sprachsensibel ausgearbeitet
❱24Q4❱ ➜ kira.dzlm-material
Kira: "Kinder rechnen anders." Mathe - mehr als Ausrechnen befasst sich schwerpunktmäßig mit den prozessbezogenen Kompetenzen des Mathematikunterrichts (Problemlösen/kreativ sein, Argumentieren, Modellieren und Darstellen/Kommunizieren
❱24Q3❱ ➜ mathematikalpha-de-fachwoerterbuch
Fachwörterlisten für Mathematik: Fremdsprache → Deutsch: Bulgarisch (6000 Begriffe, 59 Seiten) // Dänisch (9000 Begriffe, 93 Seiten) // Englisch (14000 Begriffe, 143 Seiten) // Esperanto (10000 Begriffe, 94 Seiten) // Finnisch (7000 Begriffe, 78 Seiten) // Französisch (14000 Begriffe, 157 Seiten) // Griechisch (6000 Begriffe, 61 Seiten) // Hebräisch (5700 Begriffe, 49 Seiten) // Isländisch (9000 Begriffe, 86 Seiten) // Italienisch (14000 Begriffe, 155 Seiten) // Kroatisch (6000 Begriffe, 53 Seiten) // Latein (5900 Begriffe, 52 Seiten) // Niederländisch (9000 Begriffe, 97 Seiten) // Polnisch (11000 Begriffe, 110 Seiten) // Portugiesisch (8000 Begriffe, 82 Seiten) // Rumänisch (6000 Begriffe, 56 Seiten) // Russisch (19000 Begriffe, 211 Seiten) // Schwedisch (9000 Begriffe, 93 Seiten) // Serbisch (5900 Begriffe, 59 Seiten) // Slowenisch (6000 Begriffe, 65 Seiten) // Spanisch (8000 Begriffe, 86 Seiten) // Tschechisch (10000 Begriffe, 94 Seiten) // Türkisch (6000 Begriffe, 60 Seiten) // Ungarisch (6000 Begriffe, 70 Seiten) // Vietnamesisch (8000 Begriffe, 77 Seiten)
Fachwörterlisten für Mathematik: Deutsch → Fremdsprache: Bulgarisch (61 Seiten) // Dänisch (94 Seiten) // Englisch (144 Seiten) // Esperanto (99 Seiten) // Finnisch (78 Seiten) // Deutsch-Französisch (157 Seiten) // Griechisch (64 Seiten) // Hebräisch (49 Seiten) // Isländisch (87 Seiten) // Italienisch (156 Seiten) // Deutsch-Kroatisch (55 Seiten) // Latein (53 Seiten) // Niederländisch (97 Seiten) // Polnisch (116 Seiten) // Portugiesisch (83 Seiten) // Deutsch-Rumänisch (59 Seiten) // Russisch (219 Seiten) // Schwedisch (94 Seiten) // Serbisch (62 Seiten) // Slowenisch (68 Seiten) // Deutsch-Spanisch (86 Seiten) // Tschechisch (98 Seiten) // Türkisch (63 Seiten) // Ungarisch (73 Seiten) // Vietnamesisch (80 Seiten)
❱24Q4❱ ➜ mediator-programme
Förderprogramme: Norbert Römer stellt eigene Mediator-Übungsprogramme für den Erstrechenunterricht zum Download bereit
❱24Q4❱ ➜ mathewortschatz.schule
Interaktiver Wortschatztrainer für mathematische Fachbegriffe - deutsch, türkisch-slowenisch-kroatisch-englisch-tschechisch-ungarisch mit Fachwortlisten Mathematik zu den einzelnen Sprachen als PDF-Dateien
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe_wortschatz
Mathe-Wortschatz mit Abbildungen Bild deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_de
Mathe-Wortschatz alphabetisch deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_tu
Mathewortschatz Deutsch-Türkisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_tu_d
Mathewortschatz Türkisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_slo
Mathewortschatz Deutsch-Slowakisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_slo_d
Mathewortschatz Slowakisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_kr
Mathewortschatz Deutsch-Kroatisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_kr_d
Mathewortschatz Kroatisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_en
Mathewortschatz Deutsch-Englisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_en_d
Mathewortschatz Englisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_cz
Mathewortschatz Deutsch-Tschechisch
❱24Q4❱ ➜ mathewortschatz.schule.at/woerterbuecher/mathe.wortschatz_cz_d
Mathewortschatz Tschechisch-Deutsch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_hu
Mathewortschatz Deutsch-Ungarisch
❱24Q4❱ ➜ mathewortschatz.schule-woerterbuecher-mathe.wortschatz_hu_d
Mathewortschatz Ungarisch-Deutsch
Darstellung der Rechenverfahren / Rechenwege international
Kinder, die aus anderen Herkunftsländern stammen, verwenden oft abweichende Schreibweisen für die schriftlichen Rechenverfahren. Dies stellt uns als Lehrer bei der Korrektur vor die Aufgabe, innerhalb dieser Darstellung den Fehler bei falschen Ergebnissen zu finden, um die Schüler beim Finden des korrekten Lösungsweges unterstützen zu können. Im Folgenden sind mehrere Varianten dargestellt.❱22Q1❱ ➜ uni-due-prodaz-seiteneinsteiger
Übersicht schriftlicher Rechenverfahren verschiedener Herkunftsländer
Daraus folgende Verweise auf detaillierte Darstellungen:
- Afghanistan
- Ägypten
- Algerien
- Bulgarien
- China
- Deutschland
- England
- Frankreich
- Griechenland
- Indien
- Irak
- Kroatien
- Mexiko
- Portugal
- Russland
- Spanien
- Syrien
- Türkei
- Ungarn
Vedische Mathematik
❱22Q1❱ ➜ matheknueller-deMatheknüller: Rechnen wie die alten Inder - Vedische Mathematik, eine (fast) vergessene Wissenschaft - und mehr
❱22Q1❱ ➜ de-wikipedia-org-Vedische-Mathematik-Rechenmethoden
Vedische Rechenverfahren in der Wikipedia
Vorzeichenwechsel / Klammern
- - Ich sage immer die Wahrheit
- Ich sage niemals die Unwahrheit.
- Ich habe noch nie nicht die Unwahrheit gesagt - - Peter isst niemals keinen Kaugummi
- - Wer Angst hat, ist immer vorsichtig.
- Wer Angst hat, ist nie unvorsichtig - - Nichts ist unmöglich!
Rechnen mit Größen
➜ Abschnitt ansehen / wegblenden
Größen- + Maßumwandlungen
Umrechnungsprogramme online➜ Abschnitt ansehen / wegblenden
❱24Q4❱ ➜
allesumrechnen-de
Hier kann verschiedene Zahlen, Größen usw. online um- und ausrechnen lassen: BMI Rechner - Dreisatz-Rechner - Einheiten - Filmempfindlichkeit - Kreditrechner - Carsharing - Promillerechner - Satz des Pythagoras - Spritrechner - Stromkostenrechner - Währungsrechner - Weltuhr - Zahlensysteme
❱??❱ ➜ interaktiv-lernen-net-massumwandlungen
Maßumwandlungen interaktiv
❱??❱ ➜ interaktiv-lernen-net-mathematik-freiarbeitsmaterial-Kartei_Massumwandlungen-pdf
Freiarbeitskartei Maßumwandlungen interaktiv (53 Seiten mit Lösungen)
Hier kann verschiedene Zahlen, Größen usw. online um- und ausrechnen lassen: BMI Rechner - Dreisatz-Rechner - Einheiten - Filmempfindlichkeit - Kreditrechner - Carsharing - Promillerechner - Satz des Pythagoras - Spritrechner - Stromkostenrechner - Währungsrechner - Weltuhr - Zahlensysteme
❱??❱ ➜ interaktiv-lernen-net-massumwandlungen
Maßumwandlungen interaktiv
❱??❱ ➜ interaktiv-lernen-net-mathematik-freiarbeitsmaterial-Kartei_Massumwandlungen-pdf
Freiarbeitskartei Maßumwandlungen interaktiv (53 Seiten mit Lösungen)
Rechnen mit Gewicht
➜ Abschnitt ansehen / wegblenden
❱24Q4❱ ➜
schulportal-thueringen-web-media-tspi=5180
Mathe mit Mieze Mia - Längen, Zeit, Geld, Gewichte, Allgemeines - mehrere PDF-Arbeitsblätter (Schulportal Thüringen)
❱24Q4❱ ➜ westermann-fachzeitschriften-download-pgru_05_2013
Einführung Thema "Gewicht" - Probeartikel aus der Zeitschrift 'Grundschule'
1 Gummibärchen wiegt ca. 2g
1 Schokoriegel -> 10g
1 Semmel -> 50g
1 Tafel Schokolade -> 100g
1 Päckchen Butter -> 250g
1 Packung Margarine -> 500g
1 Packung Mehl/Zucker -> 1kg
Mathe mit Mieze Mia - Längen, Zeit, Geld, Gewichte, Allgemeines - mehrere PDF-Arbeitsblätter (Schulportal Thüringen)
❱24Q4❱ ➜ westermann-fachzeitschriften-download-pgru_05_2013
Einführung Thema "Gewicht" - Probeartikel aus der Zeitschrift 'Grundschule'
Tipps
Vergleichsgewichte finden lassen:1 Gummibärchen wiegt ca. 2g
1 Schokoriegel -> 10g
1 Semmel -> 50g
1 Tafel Schokolade -> 100g
1 Päckchen Butter -> 250g
1 Packung Margarine -> 500g
1 Packung Mehl/Zucker -> 1kg
Mein kostenloses Online-Werkstattbuch zu "fast vergessenen" künstlerischen Techniken.
Wie? Gratis?
Ja. Gratis. Lernt 'was Neues!
Kunst trifft Alchemie.
Frohes Stöbern!
180 Seiten online.
Tipps für Tiefdruck, Flachdruck, analoge Fotografie, Cyanotypie, Farbherstellung, Papier schöpfen, Galvanik, Kunstgeschichte ... ein weites Feld ...
Bruchrechnung - Prozentrechnung
➜ Abschnitt ansehen / wegblenden
Medien selbst gebaut
- Deckel der Pizzaschachtel laminieren und zerschneiden
- Poolnudeln mit Cuttermesser zerschneiden. 1 Poolnudel gibt 4 Ganze. Zerkleinern bis sechstel. Für Gruppenarbeit
- Papier-Metermaß aus dem Baumarkt zerteilen lassen
- Aus drei Lackritzschnecken vier gleich große stücke herstellen lassen
- Ein Geobrett von den Schülern nageln lassen, dann mit Fäden dem geobrett spannen lassen, halbieren, vierteln ... und auf dem aufgelegten Papier einzeichnen
Einstiege für Gleichmächtigkeit
- Witziger Einstieg: "Ich bin jetzt auf Diät. Früher habe ich 8 Pizzastücke gegessen. Jetzt esse ich nur noch drei!" (Jeweils eine ganze zerteilte Pizza zeigen)
- Farbverteilung an 2 verschiedenen Glücksrädern
- Gleich geformte Gefäße mit unterschiedlichen Füllhöhen
Aktive Anwendungen
- Schüler sollen Cocktails mixen. Es darf maximal ein Fünftel Saft verwendet werden. Peter verwendet 1/10 l Apfelsaft, 3/40 l Mangosaft und 1/20 l Maracujasaft. Hat er die Vorgabe eingehalten?
- Einzige lebensnahe Anwendung: Einsatz zur Nutzung von Rechenvorteilen. Du musst eine Zahl durch 36 teilen und das Ergebnis mit 18 multiplizieren? Nimm doch einfach die Hälfte!
❱23Q2❱ ➜
bildungsserver-berlin-brandenburg-de-imint-grundschule-themenkisten-brueche
Themenkiste "Brüche" am Bildungsserver Berlin-Brandenburg -Unterrichtsmaterialien und Plakate zum Download
❱24Q4❱ ➜ bruchrechnen-de
Bruchrechnen. Hier lernst du, wie man typische Fehler beim Bruchrechnen vermeidet. Die wichtigsten Regeln auf einen Blick. Im Übungskurs zum Bruchrechnen lernst du alles über den Umgang mit Kehrwerten, Hauptnennern und dergleichen mehr
❱24Q4❱ ➜ archive-org-digitale-schule-bayern-dsdaten-198-5
1 Seite Merkblatt zu Ablaufschritten der Addition/Subtraktion/Multiplikation und Division von Brüchen
❱24Q4❱ ➜ archive-org-edupic-net/math_gr-fractions
(Archive-org) Abbildungen / Bilder für Bruchdarstellungen: Pizza, Kuchen, geometrische Figuren (längere Ladezeit, da aus archive-org eingebunden)
❱24Q4❱ ➜ grzesina-physik-versuche-panfloete
Anwendung der Bruchrechnung: Bau einer Panflöte - mit Berechnung der Pfeifenlängen und Frequenzen
❱24Q4❱ ➜ interaktiv-lernen-net-id=13&Itemid=108
Arbeitsblätter für 5.-8.Jahrgangsstufe. Zahlensystem, Dezimalbrüche, Bruchrechnen, Ganze Zahlen, Grundrechenarten, Tabellen zum Eintragen von Flächenmaßen / Längenmaßen
❱24Q4❱ ➜ univie.ac-future.media-mo
Mathematische Puzzles zum Selbermachen Dies ist ein Applet in Form eines Puzzles, dessen Inhalt Sie für Ihre eigenen Zwecke selbst gestalten können. Die Eingabeseite für die automatische Erzeugung von Puzzles befindet sich auf der Website von mathe online:
❱23Q2❱ ➜ mathetoolbar-de
Tafelbilder und interaktive Übungen zu Bruchrechnung und Dezimalzahlen
❱24Q4❱ ➜ archive-org-mond-mathe-boerse-Bruch
Arbeitsblätter Bruchrechnen Hauptschule - (längere Ladezeit, da aus archive-org eingebunden)
❱24Q4❱ ➜ tb-u-de-boerse-s_ma1.html#arbeitsblatter-bruchrechnen
Arbeitsblätter zum Bruchrechnen - Tauschbörse Unterricht
❱24Q4❱ ➜ tb-u-boerse-s_ma2.html#begriffe-errechnen-bruchrechnung
Begriffe errechnen: Brüche, Arbeitsblätter
❱24Q4❱ ➜ tb-u-boerse-s_ma3.html#lochkarten-bruchrechnung
Lochkarten zur Bruchrechnung
❱24Q4❱ ➜ unterrichten.zum-de-wiki-Grundwissen-Brüche
Grundwissen Bruchrechnung
❱24Q4❱ ➜ unterrichten.zum-de-wiki-Kategorie:Mathematik
Kategorie 'Mathematik' bei unterrichten.zum
Aufgabenbeispiele / Darstellungen mit Geogebra
❱24Q4❱ ➜ geogebra-org-arithmetic
Interaktive Darstellungen und Aufgaben zur Arithmetik (Geogebra)
❱24Q4❱ ➜ geogebra.org/search/Bruch
Brüche darstellen, kürzen, erweitern ... - interaktive Darstellung mit Geogebra
❱24Q4❱ ➜ unterrichten-zum-Grundwissen_-_Brüche
Grundwissen Brüche bei ZUM
❱24Q4❱ ➜ unterrichten-zum-Mathematik-digital
Digitale Anwendungen zum Bruchrechnen - siehe Klasse 6
Themenkiste "Brüche" am Bildungsserver Berlin-Brandenburg -Unterrichtsmaterialien und Plakate zum Download
❱24Q4❱ ➜ bruchrechnen-de
Bruchrechnen. Hier lernst du, wie man typische Fehler beim Bruchrechnen vermeidet. Die wichtigsten Regeln auf einen Blick. Im Übungskurs zum Bruchrechnen lernst du alles über den Umgang mit Kehrwerten, Hauptnennern und dergleichen mehr
❱24Q4❱ ➜ archive-org-digitale-schule-bayern-dsdaten-198-5
1 Seite Merkblatt zu Ablaufschritten der Addition/Subtraktion/Multiplikation und Division von Brüchen
❱24Q4❱ ➜ archive-org-edupic-net/math_gr-fractions
(Archive-org) Abbildungen / Bilder für Bruchdarstellungen: Pizza, Kuchen, geometrische Figuren (längere Ladezeit, da aus archive-org eingebunden)
❱24Q4❱ ➜ grzesina-physik-versuche-panfloete
Anwendung der Bruchrechnung: Bau einer Panflöte - mit Berechnung der Pfeifenlängen und Frequenzen
❱24Q4❱ ➜ interaktiv-lernen-net-id=13&Itemid=108
Arbeitsblätter für 5.-8.Jahrgangsstufe. Zahlensystem, Dezimalbrüche, Bruchrechnen, Ganze Zahlen, Grundrechenarten, Tabellen zum Eintragen von Flächenmaßen / Längenmaßen
❱24Q4❱ ➜ univie.ac-future.media-mo
Mathematische Puzzles zum Selbermachen Dies ist ein Applet in Form eines Puzzles, dessen Inhalt Sie für Ihre eigenen Zwecke selbst gestalten können. Die Eingabeseite für die automatische Erzeugung von Puzzles befindet sich auf der Website von mathe online:
❱23Q2❱ ➜ mathetoolbar-de
Tafelbilder und interaktive Übungen zu Bruchrechnung und Dezimalzahlen
❱24Q4❱ ➜ archive-org-mond-mathe-boerse-Bruch
Arbeitsblätter Bruchrechnen Hauptschule - (längere Ladezeit, da aus archive-org eingebunden)
❱24Q4❱ ➜ tb-u-de-boerse-s_ma1.html#arbeitsblatter-bruchrechnen
Arbeitsblätter zum Bruchrechnen - Tauschbörse Unterricht
❱24Q4❱ ➜ tb-u-boerse-s_ma2.html#begriffe-errechnen-bruchrechnung
Begriffe errechnen: Brüche, Arbeitsblätter
❱24Q4❱ ➜ tb-u-boerse-s_ma3.html#lochkarten-bruchrechnung
Lochkarten zur Bruchrechnung
❱24Q4❱ ➜ unterrichten.zum-de-wiki-Grundwissen-Brüche
Grundwissen Bruchrechnung
❱24Q4❱ ➜ unterrichten.zum-de-wiki-Kategorie:Mathematik
Kategorie 'Mathematik' bei unterrichten.zum
Software / interaktiv
❱24Q4❱ ➜ geogebra-org-jHCA8jfGAufgabenbeispiele / Darstellungen mit Geogebra
❱24Q4❱ ➜ geogebra-org-arithmetic
Interaktive Darstellungen und Aufgaben zur Arithmetik (Geogebra)
❱24Q4❱ ➜ geogebra.org/search/Bruch
Brüche darstellen, kürzen, erweitern ... - interaktive Darstellung mit Geogebra
❱24Q4❱ ➜ unterrichten-zum-Grundwissen_-_Brüche
Grundwissen Brüche bei ZUM
❱24Q4❱ ➜ unterrichten-zum-Mathematik-digital
Digitale Anwendungen zum Bruchrechnen - siehe Klasse 6
Zuordnungen - Prop-Antiprop
➜ Abschnitt ansehen / wegblenden
Proportional
- Je höher die angelegte Spannung an einem Widerstand ist, umso höher ist die gemessene Stromstärke am Widerstand
- Je länger eine Außenbeleuchtung brennt, umso höher ist der Stromverbrauch. (Achtung: Nicht unbedingt auch die Kosten, denn Energieversorger bieten Staffelpreise an)
- Je mehr Kohlenstoff verbrannt wird, umso mehr Sauerstoff wird verbraucht und umso mehr CO2 entsteht
- Je größer die Summe der Außenkanten eines Quaders ist, umso größer ist (bei konstanter Höhe) das Volumen
- Je höher das Wasser in einem (quaderförmigen oder runden) Schwimmbecken steht, umso größer ist das Wasservolumen
- Je höher das Wasser in einem (quaderförmigen oder runden) Schwimmbecken steht, umso größer ist der Energiebedarf zur Erwärmung
- Je größer der Rohrquerschnitt eines Ablassrohres ist, umso größer ist der Wasserabfluss
- Schriftgröße: Je größer die Schriftart (in pt), umsomehr Blätter werden benötigt, um denselben Text zu setzen
Antiproportional
Neben den beliebten Aufgabenstellungen mit Arbeitern und Maschinen. Diese Beispiele gehen jedoch irgendwann ins Absurde, da die sich ab einer gewissen Menge gegenseitig behindern und das "je mehr-desto weniger Zeit" nicht mehr zutrifft. Zudem können Schüler das auch proportional betrachten: "Je mehr - umso schneller..."- Papier zerschneiden: Je mehr Stücke ich aus einem Bogen mache, desto kleiner werden die Stücke
- Lottospieler: Je mehr Teilnehmer in der Tippgemeinschaft sind, umso geringer wird der Anteil bei einem Gewinn
- Luft: Je mehr Menschen in einem Raum sind, umso weniger Sauerstoff bleibt pro Person
- Querschnitt: Je größer der Rohrquerschnitt eines Ablassrohres ist, umso größer ist der Wasserabfluss (desto weniger Zeit wird benötigt)
- Geschwindigkeit: Je höher die durchschnittliche Geschwindigkeit, desto geringer die benötigte Zeit
- Fläche: Je größer die Fläche einer Fliese / eines Brettes ist, umso weniger Fliesen / Bretter werden für die zu belegende Fläche benötigt (wenn kein Verschnitt anfällt)
Geometrie - Geometrische Körper
Volumina und Satz des Pythagoras➜ Abschnitt ansehen / wegblenden
Zu Geometrie ➜ siehe auch
kunstunterricht.htm#Golden Goldener Schnitt
Die ägyptische Knotenschnur
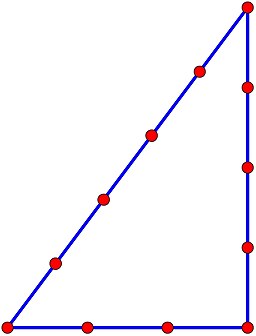
Abbildung via Wikimedia Commons
Die "Ägyptische Knotenschnur" wird auch als Zwölfknotenschnur, 13-Knotenschnur, Maurerdreieck, Bauwinkel, Winkeldreieck, "3-4-5-Dreieck" bezeichnet. Etwas verwirrend erscheint zunächst die Bezeichnung als 12- bzw. 13-Knotenschnur. Die Verwirrung lässt sich dadurch lösen, dass nicht die Anzahl der Knoten, sondern die 12 Längenabschnitte maßgeblich sind. Bei der "12-Knotenschnur" fallen Anfangs- und Endknoten aufeinander - das Seil ist zur Schlaufe verbunden. Ein mit der Schnur gebildetes Dreieck mit den Seitenlängen 3-4-5 ergibt ein rechteckiges Dreieck (Pythagoras: 3²+4²=5²). Die Knotenschnur wurde bereits in Ägypten (daher der Name) für die Geometrie im Gelände verwendet.
Ein aus der ägyptischen Kontenschnur "... gebildeter Kreis hat einen Durchmesser von knapp einem Drittel (genauer einem Pi-tel) der Schnurlänge, und der Winkelabstand benachbarter Punkte beträgt vom Kreismittelpunkt aus gesehen genau 30 Bogengrad. Das aus der Schnur gebildete gleichseitige Dreieck hat eine Basislänge von einem Drittel der Schnurlänge sowie drei Eckwinkel von genau 60 Bogengrad." Somit kann die Knotenschnur nicht nur zur Konstruktion eines rechten Winkels im Gelände dienen. Man kann damit auch Strecken halbieren, dritteln, vierteln und sechsteln (s.Abb.). In der Abbildung ist ersichtlich, dass bei der Streckenteilung eigentlich ein 13. Knoten am Ende des Seiles Sinn macht.

Herstellungstipps
Nehmt eine (etwas stabilere, aber nicht zu dicke) Schnur und teilt diese durch Knoten in 12 gleich lange Abschnitte ein. Ich habe die Abschnitte für die Schüler bewusst verschieden lang gewählt, damit die Allgemeingültigkeit des Verfahrens deutlich wird - und man im Anschluss mit verschiedenen gemessenen Längen den Pythagoras nachweisen kann.Schnurvarianten (je 5 Exemplare)
- 12 Abschnitte mit jeweils 25 cm (Gesamtlänge der Knotenschnur dadurch 3 Meter)
- 12 Abschnitte mit jeweils 30 cm (Gesamtlänge der Knotenschnur 3,60 Meter)
- 12 Abschnitte mit jeweils 40 cm (Gesamtlänge der Knotenschnur 4,80 Meter)
- 12 Abschnitte mit jeweils 50 cm (Gesamtlänge der Knotenschnur 6 Meter)
Somit stehen 20 Knotenschnüre zur Verfügung. Damit diese möglichst präzise und für mehrere Jahre verwendbar sind, ist das Lehrerarbeit. Die Knotenschnüre bewahre ich mit Haargummis zusammengebunden in Ziptüten "verwurschtelungsfrei" auf.
Aufgabe für jeweils 4 Schüler (einer pro "Ecke" + ein Zeichner): Konstruiert ein rechteckiges "Blumenbeet", bzw. den Rahmen für eine Baugrube auf den Hof. Spannt die Knotenschnur so zu einem Dreieck, dass sich auf einer Seite 3 Abschnitte, auf einer 4 und auf der dritten Seite 5 Abschnitte befinden und die Endknoten sich wieder berühren. Der Zeichner umfährt dann das gespannte Dreieck auf den Schulhof mit Kreide. Dann muss die Schnur nochmals so gespannt werden, dass die längste Seite auf der gezeichneten längsten Seite liegt und sich beim Spannen nun ein Rechteck ergibt.
Konstruiert zwei verschieden große Rechtecke. Messt die Seitenlängen und notiert diese.
Die gemessenen Seitenlängen dienen später im Klassenzimmer zum Rechnen mit dem Satz des Pythagoras.
- ➜ de.wikipedia.org-Zwölfknotenschnur
Die "Ägyptische Knotenschnur" oder "12-Knotenschnur" als Hilfsmittel zur Herstellung rechter Winkel im Gelände
Linktipps zur Knotenschnur
❱22Q1❱ ➜ mathematik-bildung-rp-de-Vom_rechten_Seilspannen-pdfVom rechten Seilspannen. Unterrichtseinheit zum Satz des Pythagoras
❱23Q2❱ ➜ chatta-ch-mit-003_2000-pdf
"Die Schnurvermessung im mittelalterlichen Bauwesen" von Rudolf Moosbrugger-Leu, 32 Seiten PDF
❱22Q1❱ ➜ vermessungsgeschichte-de-Knoten-pdf
Helmut Minow: Vemessungen mit der Zwölfknotenschnur und anderen historische Konstruktionen mit dem Meßseil, Dortmund 1992. 25 Seiten PDF. Darin wird auch beschrieben, wie mit der Knotenschnur Ellipsen, Quadrate, Rechtecke, Fünfecke... konstruieren lassen.
❱22Q1❱ ➜ de.wikipedia.org-Pythagoreisches_Tripel
Pythagoreische Tripel bezeichnen die drei natürlichen Zahlen, die als Längen der Seiten eines rechtwinkeligen Dreiecks vorkommen können.
Auf dieser Wikipedia-Seite werden weitere Tripel angegeben und die Methode zu deren Berechnung erläutert.
Der einfachste Pythagoreische Tripel ist 3-4-5, denn 32 + 42 = 52
weitere (primitive) Tripel (geordnet nach der längsten Seite c):
(3, 4, 5) (5, 12, 13) (8, 15, 17) (7, 24, 25) (20, 21, 29) (12, 35, 37) (9, 40, 41) (28, 45, 53) (11, 60, 61) (16, 63, 65) (33, 56, 65) (48, 55, 73) (13, 84, 85) (36, 77, 85) (39, 80, 89) (65, 72, 97) (20, 99, 101) (56, 90, 106) (60, 91, 109) (15, 112, 113) (44, 117, 125) (88, 105, 137) (17, 144, 145) (24, 143, 145) (51, 140, 149) (85, 132, 157) (119, 120, 169) (52, 165, 173) (19, 180, 181) (57, 176, 185) (104, 153, 185) (95, 168, 193) (28, 195, 197) (84, 187, 205) (133, 156, 205) (21, 220, 221) (140, 171, 221) (60, 221, 229) (105, 208, 233) (120, 209, 241) (32, 255, 257) (23, 264, 265) (96, 247, 265) (69, 260, 269) (115, 252, 277) (160, 231, 281) (161, 240, 289) (68, 285, 293)
Primitive pythagoreische Tripel (a,b,c) sind solche, für die a, b und c keinen gemeinsamen Teiler außer 1 haben. Durch Multiplikation der Tripelzahlen (Verdoppelung, Verdreifachung ...) ergeben sich weitere Tripel. Die Liste ist nicht vollständig. Weitere siehe Link zur Wikipedia. Dort sind auch die Berechnungsmethoden beschrieben.
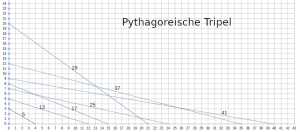
Darstellung der pythagoreischen Tripel als Suchdiagramm im Koordinatensystem. Nicht-primitive Tripel (Vielfache) ergeben eine Parallelenschar zu den primitiven Tripeln.
Wikipedia-Artikel zu Pythagoras
- ➜ de.wikipedia.org-Satz_des_Pythagoras
- ➜ commons.wikimedia.org-File:01-Satz_des_Pythagoras-W.gif
In dieser Gif-Animation wird die Flächengleichheit als Füllen mit Flüssigkeit dargestellt
Links zu Pythagoras
❱24Q4❱ ➜ cut-the-knotInteractive Mathematics Miscellany and Puzzles - Hier sind nicht weniger als 29 Beweise des Satzes von Pythagoras zusammengestellt. Zusätzlich gibt es eine kleine Liste mit weiterführenden Links
❱23Q1❱ ➜ geogebra-org-m-hxmjvqa7
Newton meets Pythagoras - Satz des Pythagoras per Schwerkraft dargestellt.
❱24Q4❱ ➜ lehrerfortbildung-bw-mathematik-pythagoras
Satz des Pythagoras - Leiterproblem von Romeo und Julia. Leichter zu rechnen jedoch mit 3 Meter Abstand von der Wand, weil 3² + 4² = 5²
❱24Q4❱ ➜ lehrerfortbildung-bw-mathematik-5legespiel
Satz des Pythagoras - Legespiel - Vorlage
❱24Q4❱ ➜ math.uni-bielefeld-ringel-puzzle
Auch die ähnlichen Kringel, Halbkreise, Fünfecke usw. über den Kathethen eines rechtwinkligen Dreiecks sind flächengleich.
Links
❱24Q4❱ ➜ dynageoEUKLID-Dynageo ist ein Computerprogramm zur beweglichen Geometrie". Es ermöglicht die Erstellung von dynamischen Zeichnungen, in denen Punkte nachträglich verschoben werden können, ohne dass die bei der Erstellung der Zeichnung festgelegten Zusammenhänge zwischen den geometrischen Objekten verloren gehen. Das Programm ist Shareware - eine Schullizenz ist erschwinglich.
❱24Q4❱ ➜ geogebra-cms
GeoGebra ist eine kostenlose und plattforumunabhängige dynamische Mathematik Software für Schulen, die Geometrie, Algebra und Analysis verbindet. Das Java-Programm läuft ohne Installation online. - evtl. wird noch eine Java-Runtime installiert. GeoGebra hat bereits mehrere internationale Preise gewonnen, darunter der europäische und deutsche Bildungssoftware Preis
❱24Q4❱ ➜ geometria-funktionen
Applet zur Konstruktion geometrischer Figuren
❱24Q4❱ ➜ geometrie-studio
Von der Darstellung einfacher Grundformen wie Dreiecke oder Quadrate bis hin zur Kombination mehrerer Funktionsterme findet man hier ein breites Spektrum interaktiver, geometrischer Anwendungen
❱24Q4❱ ➜ korthalsaltes
Geometrische Körper - Sterne, Plygone usw als Schnittmuster
❱24Q4❱ ➜ mathe-werkstatt-index1
Dynamische Geometrie
❱24Q4❱ ➜ mathe-werkstatt-web-download
Downloadseite für Programme und Übungsblätter / Arbeitsblätter
❱24Q4❱ ➜ mathe-werkstatt-download-brunbau
Schnittvorlagen für geometrische Körper
❱24Q4❱ ➜ matheprojekt-ph-tirol-at-mathematik-methoden
Reihe "Mathematik Methoden" zum Download: gleichungen-pythagoras-vierecke-dreieckskonstruktionen-winkel-geometrischefiguren-prozentrechnen-statistik-zeit
Filme zum Pythagoras
❱24Q4❱ ➜ youtube-v=iK9bhyl6B_EKorkator: Wie weit ist es zum Horizont? - musikalisch erklärt und berechnet in 4'50"
Platonische Körper
❱24Q4❱ ➜ 3quarks.com/de/PlatonischeKoerper/indexPlatonische Körper
❱22Q4❱ ➜ polyhedra-world-nc
A walk in the polyhedra world: Plato's five regular polyhedra
❱22Q4❱ ➜ polyhedra-world-nc-morph
Dual morphing of the regular polyhedra
❱24Q4❱ ➜ home.adelphi.edu/~stemkoski/mathematrix/platonic
Platonic Solids Mathematrix
❱24Q4❱ ➜ hbmeyer-de-flechten-index
Polyeder aus Flechtstreifen
❱24Q4❱ ➜ hbmeyer-de-flechten-indexeng
Polyhedra plaited with paper strips
❱24Q4❱ ➜ mathe-garten-de-der-mathematik-garten
Der Mathematik-Garten
❱24Q4❱ ➜ matheschmidt
Bastelbögen für Platonische Körper und Matheunterricht Klasse 5-12
❱24Q4❱ ➜ peda.com
Program for downloading - Poly is a shareware program for exploring and constructing polyhedra
❱22Q4❱ ➜ users-ph-nat-tum~gmueller
Platonische Körper in Stereodarstellung und mehr
❱24Q4❱ ➜ polyhedra-net-en
Paper Models of Polyhedra
❱24Q4❱ ➜ walter-fendt-de-m14d/platon
Die Platonischen Körper Walter Fendt (Mathematik-Applets)
❱24Q4❱ ➜ wikipedia-org-wiki-Cluster-Physik
Cluster (Physik) Wikipedia
❱24Q4❱ ➜ wikipedia-org-wiki-Platonischer-Körper
Platonischer Körper
❱24Q4❱ ➜ wikipedia-org-wiki-Platonic-solid
Platonic solid
❱22Q4:❱ ➜ spektrum-de-suche-Platonische Körper
Suchergebnis nach "Platonische Körper" auf Spektrum.de - 9062 Treffer ;-)
❱24Q4❱ ➜ library-wolfram-com-webMathematica-Graphics-Polyhedron
Polyhedron Explorer (Applet) von WolframResearch
❱24Q4❱ ➜ mathworld-wolfram-com-PlatonicSolid
Platonic Solid MathWorld
❱24Q4❱ ➜ archive-org-groups-.mcs-st-andrews-john-geometry-Lectures
Symmetry groups of Platonic solids
❱24Q4❱ ➜ zebis-ch-unterrichtsmaterial-die-fuenf-platonischen-koerper
Die fünf Platonischen Körper
Würfelnetze
➜ Abschnitt ansehen / wegblenden
Ideen
- Würfelnetze als Hüpfspiele auf dem Schulhof zeichnen. Dazu erhält jede Gruppe 6 Quadrate aus Pappe oder Sperrholz, legt die aus, umfährt sie mit Kreide und schreibt eine Spielvorschrift. Wenn man die Quadrate an den Kanten mit Klebeband aneinender klebt, kann man testen, ob sich ein Würfel ergibt.
- Wie ist der Spielwürfel aufgebaut, Punktesumme der gegenüberliegenden Seiten untersuchen. Wo liegen die "Augen" beim Auseinanderfalten zum Würfelnetz?
- Welches der 35 Hexaminos kann zu einem Würfel gefaltet werden?
❱22Q4❱ ➜ arbblatt-hexaminos_2.pdf
Hier findet ihr eine PDF mit den 35 Hexamino-Möglichkeiten
Links
❱24Q4❱ ➜ 4teachers-action-material-id=36263Lehrprobe Würfelnetze bei 4teachers
❱22Q4❱ ➜ pikas-dzlm-de-unterricht-raum-und-form-würfelnetze
Unterrichtsmaterial aus einer geometrischen Lernumgebung mit dem Thema "Würfelnetze handlungsorientiert entdecken"
❱24Q4❱ ➜ archive-org-schulen.eduhi-riedgym-mathematik-klasse1-raumvorstellung
Online-Test zu den Würfelnetzen - (längere Ladezeit, da aus archive-org eingebunden)
❱24Q4❱ ➜ frustfrei-lernen-de-mathematik-wuerfelnetze
Filmchen und Arbeitsblätter
❱24Q4❱ ➜ grundschulmarkt-mathe-wuerfelnetze
PDF mit Würfelnetzen
❱24Q4❱ ➜ mathematikus
Interaktive Seite zur räumlichen Vorstellung. Würfelnetze, Würfel zerlegen, Schnittmuster für räumliche Körper, Würfel kippen ... whiteboardgeeignet
❱24Q4❱ ➜ mildner-web-de-Roland-triowuer
Trio-Würfel (Dreifarben-Bauwürfel)
❱24Q4❱ ➜ montessori-download-de-wuerfelnetze/
Arbeitsblätter mit Ausschneidebögen
❱24Q4❱ ➜ oesi-mediennutzung-klasse3-wuerfelnetz
Lehrprobe Herstellung von Würfelnetzen - Klasse 3
❱24Q4❱ ➜ oesi-mediennutzung-klasse4-wuerfelnetze
Lehrprobe Wir suchen Würfelnetze - Klasse 4
❱24Q4❱ ➜ raetseldino-de-logikraetsel-welche-figuren-sind-wuerfelnetze
Rätsel zu Würfelnetzen - Arbeitsblatt
Koordinatensystem / Kartesisches System
➜ Abschnitt ansehen / wegblenden
Beispiele zur Einführung
- Kino: Reihe x, Platz y, x-Achse ist der Gang, y-Achse die Leinwand
- Schatzsuche mit Längenangaben - "gehe 5 schritte nach rechts, dann 3 noch oben" kann jedoch verwirren, weil man sich nicht in die Höhe bewegt
- Häuser: Hausnummer x und Stockwerk y
- Schiffe versenken - hier wird jedoch mit Buchstaben/Zahlen hantiert - kann verwirren
- Tabellenkalkulation - hier wird ebenfalls mit Buchstaben/Zahlen hantiert - kann verwirren
- Koordinatensystem am Boden aufkleben und Schüler stellen sich selbst als Punkte auf
- Pokemon-Jagd) : Koordinatensystem auf dem Boden abkleben, SuS müssen Position der Pokemon nennen und die Wege abgehen: x-Achse entlang krabbeln, y-Achse hüpfen
Zahlensysteme, Römische Zahlen, Primzahlen + Zahlenreihen
➜ Abschnitt ansehen / wegblenden
➜ siehe auch
geschichte0-Romer Römische Geschichte
➜ siehe auch Mathefaszination Zehner-Potenzen und Faszinierendes, sowie Anekdoten zur Mathematik
➜ siehe auch kunstunterricht-Golden Goldener Schnitt / Fibanocci-Reihe
➜ siehe auch Mathefaszination Zehner-Potenzen und Faszinierendes, sowie Anekdoten zur Mathematik
➜ siehe auch kunstunterricht-Golden Goldener Schnitt / Fibanocci-Reihe
Ausmalbilder / Zahlenreihen
❱22Q4❱ ➜ hugolescargot-com-fiches-scolaires-mathsAusmalbilder - Zahlenreihen-Bilder, Arbeitsblätter (Verbinden von Zahlenreihen) - ziemlich werbeüberfrachtet, französische Seite
Zahlbereichserweiterung / Zahlsysteme
❱24Q4❱➜ siehe auch autenrieths-haupt-mathe-grosse_zahlenEin Lichtjahr in Kilometern und Bezeichnungen für große Zahlen
❱24Q4❱➜ siehe auch autenrieths-planetenpfad_entfernungen_im _modell
Umrechnungstabelle zur Berechnung der Größenverhältnisse und Entfernungen zum Anlegen eines Planetenpfades - oder zur Veranschaulichung der Größenverhältnisse in unserem Planetensystem. Damit Sie diese Tabelle bearbeiten können - und einen eigenen Sonnendurchmesser eintragen können - müssen Sie die Tabelle zunächst abspeichern.
❱24Q4❱ ➜ allesumrechnen-zahlensysteme_umrechnen
Hier kann man Zahlen online in beide Richtungen zwischen verschiedenen Zahlsystemen umrechnen - binär, oktal, duodezimal bis hexadezimal
❱24Q4❱ ➜ 4teachers-action=material-id=20156
Zahlbereichserweiterung, Umwandeln von Zahlwörtern in Zahlen, ermitteln von Zahlen durch Bündeln und Tauschen, Arbeit im Stellenwertordner. geignet für die 5. Klasse
Primzahlen
➜ siehe auch Mathefaszination - Primzahlen❱24Q4❱ ➜ lehrer-uni-karlsruhe-de-primosthenes
Das Gefängnis von König Primostenes - eine Darstellung des Siebes des Erasthones zur Berechnung der Primzahlen
❱24Q4❱ ➜ t5k-org
Homepage zu Primzahlen
Römische Zahlen
❱24Q4❱ ➜ 4teachers-action=show&id=6205Mehrere Materialien zu Römischen Zahlen bei 4teachers
❱24Q4❱ ➜ diaware-htmlroemzahl
Römische Zahlen - Regeln und Umrechner, Verweis auf Arbeitsblätter
❱24Q4❱ ➜ mathepower.com/roemisch
Römischer Online - Compvter - Taschenrechner
❱22Q4❱ ➜ blog-stevenlevithan-javascript-roman-numeral-converter
Java-Script-Code für einen Umrechner von römischen Zeichen
❱24Q4❱ ➜ vs-material.wegerer-sachkunde-roem_arab_ziffern
Zeichenerklärung Römische Zahlen / Arbeitsblatt
Wikipedia-Artikel
- ➜ de.wikipedia-wiki-Zahlennamen
Aufbau von Zahlennamen und die Benennung von Zahlen im Dezimalsystem - Wie nennt man eine Zahl mit 17 Nullen?"> - ➜ de-wikipedia-org-wiki-Römische_Zahlschrift
Römische Zahlen - ➜ commons-wikimedia-org-wiki-Category:Roman_numerals
Abbildungen römischer Zahlen
Literatur
❱24Q3🛒 [Affiliate-Link] ➜ 6000 Jahre MathematikEine kulturgeschichtliche Zeitreise - 1. Von den Anfängen bis Leibniz und Newton (Vom Zählstein zum Computer)
Matheunterricht Fachportale + FB-Gruppen
Linklisten zu Mathematik + Mathedidaktik➜ Abschnitt ansehen / wegblenden
❱24Q4❱ ➜
bildungsserver-elixier-Mathematikunterricht
280 Treffer bei Suche nach "Mathematik" in Onlineressourcen der Bildungsserver. Dort werden jedoch auch Filme der Kreismedienzentren und kostenpflichtige Verlagsprodukte verlinkt - Perlen muss man selbst suchen
❱23Q4❱ ➜ facebook-com-groups-466096550211509
Facebook: Unterrichtsideen Mathematik
❱24Q4❱ ➜ mathematikunterricht-sitemap
Ka's Geometriepage & Mathe-Galerie - sehr umfangreich - letztes Update jedoch 2001
❱24Q4❱ ➜ schule-bw-unterricht-faecher-mathematik (auch: mathematik-bw)
Materialien und Links im Mathematik-Portal vom Landesbildungsserver Baden-Württemberg
❱24Q4❱ ➜ unterrichten-zum-wiki-Mathematik
Mathematik am ZUM-Server
❱24Q4❱ ➜ unterrichten-zum-de-Kategorie:Mathematik
Kategorie:Mathematik am ZUM-Server
280 Treffer bei Suche nach "Mathematik" in Onlineressourcen der Bildungsserver. Dort werden jedoch auch Filme der Kreismedienzentren und kostenpflichtige Verlagsprodukte verlinkt - Perlen muss man selbst suchen
❱23Q4❱ ➜ facebook-com-groups-466096550211509
Facebook: Unterrichtsideen Mathematik
❱24Q4❱ ➜ mathematikunterricht-sitemap
Ka's Geometriepage & Mathe-Galerie - sehr umfangreich - letztes Update jedoch 2001
❱24Q4❱ ➜ schule-bw-unterricht-faecher-mathematik (auch: mathematik-bw)
Materialien und Links im Mathematik-Portal vom Landesbildungsserver Baden-Württemberg
❱24Q4❱ ➜ unterrichten-zum-wiki-Mathematik
Mathematik am ZUM-Server
❱24Q4❱ ➜ unterrichten-zum-de-Kategorie:Mathematik
Kategorie:Mathematik am ZUM-Server
Faszinierendes, Spaßiges + Musik im Mathe-Unterricht
➜ Abschnitt ansehen / wegblenden
❱24Q4❱ ➜
mathematische-basteleien-de/
Basteleien und Faltarbeiten: Papierarbeiten, Schreibspiele, Würfelpuzzles, Zahlenspielereien, Computern, Vielecke, Figuren, Kurven, Regelmäßige Körper,
❱22Q4❱ ➜ stauff-matgesch-dateien-mathe
Anschauliche Mathematik: Die andere Seite der Mathematik, Zauberreich Naturwissenschaften, Bewegte Mathematik, JAVA-Applets
Suchergebnis: "Cool Math Songs"
Basteleien und Faltarbeiten: Papierarbeiten, Schreibspiele, Würfelpuzzles, Zahlenspielereien, Computern, Vielecke, Figuren, Kurven, Regelmäßige Körper,
❱22Q4❱ ➜ stauff-matgesch-dateien-mathe
Anschauliche Mathematik: Die andere Seite der Mathematik, Zauberreich Naturwissenschaften, Bewegte Mathematik, JAVA-Applets
Lieder - Mathe mit Musik
❱21❱ ➜ duckduckgo-com-cool+math+songsSuchergebnis: "Cool Math Songs"
Dyskalkulie / Rechenschwäche / Arithmasthenie / Rechenstörung
➜ Abschnitt ansehen / wegblenden
➜ siehe auch
weiter oben bei 'Grundrechenarten
➜ siehe auch Nachteilsausgleich
➜ siehe auch Rechenverfahren in Herkunftsländern von Migranten und Geflohenen
➜ siehe auch Nachteilsausgleich
➜ siehe auch Rechenverfahren in Herkunftsländern von Migranten und Geflohenen
❱24Q4❱ ➜
arbeitsblaetter-kat=SD
Symptomtraining - Kostenlose Arbeitsblätter für das tägliche Mathe-Training zum Download (mehr als 6900 Seiten!)
❱24Q4❱ ➜ bildungsserver.berlin-brandenburg-de-mathematik-praevention_rechenstoerungen-schipper_material_rechenstoerungen.pdf
18 Seiten PDF: Übungen bei Rechenstörungen für Schüler Klasse 1-5
❱24Q4❱ ➜ dyskalkulie-marburg-de-symptome-dyskalkulie-14
Diagnosebogen Dyskalkulie - Symptom-Katalog für Eltern
❱24Q4❱ ➜ icd-code-de-icd-code-F81.2
Dyskalkulie - Definition nach ICD-10: F80-F89 Entwicklungsstörungen / F81.2 Rechenstörung
❱24Q4❱ ➜ legakids-eltern-lehrer-lernmaterialien-kostenlose-uebungen
Seite zum Thema LRS und Rechenschwäche mit kostenlosem Unterrichtsmaterial für die Grundschule
❱23Q2❱ ➜ legasthenie-lvl-bw-de-dyskalkulie-diagnostik
Diagnose einer Dyskalkulie - Wie kann eine Dyskalkulie bei einem Kind festgestellt werden? Info vom Landesvberbans Legasthenie Ba-Wü
Arbeitskreis des Zentrums für angewandte Lernforschung gemeinnützige GmbH Rechenschwäche / Dyskalkulie
❱24Q4❱ ➜ bildungsserver.berlin-brandenburg-de-praevention-rechenstoerungen
Informationen, Materialien und Links zur Prävention von Rechenstörungen
❱24Q4❱ ➜ bildungsserver-seite=794
Linksammlung Rechenschwäche/Dyskalkulie am Dt.Bildungsserver
❱24Q4❱ ➜ opus.bsz-bw-volltexte-2007-16-gerster
Schwierigkeiten beim Erwerb mathematischer Konzepte im Anfangsunterricht - Bericht zum Forschungsprojekt 'Rechenschwäche - Erkennen, Beheben, Vorbeugen' von Hans-Dieter Gerster und Rita Schultz, PH Freiburg, 2000 (427 S. PDF)
❱24Q4❱ ➜ bvl-dyskalkulie
Bundesverband Legasthenie und Dyskalkulie e.V.
❱23Q2❱ ➜ bvl-legasthenie-de-10__Lehrer_Dyskalkulie_2020-pdf
Dyskalkulie in der Schule - 30 Seiten Handreichung vom Bundesverband Legasthenie und Dyskalkulie e.V.
❱24Q4❱ ➜ dimdi-de-dynamic-en-dimdi-for-the-public
Klassifizierung nach ICD-10 der WHO: F81.2
❱24Q4❱ ➜ familienhandbuch-schulprobleme-rechenschwache-grundschuler-ursachen-diagnose-forderung
Prof. Dr. Oliver Thiel: Rechenschwache Grundschüler - Ursachen, Diagnose, Förderung (archive.org)
❱24Q4❱ ➜ ifrk-ev
Initiative zur Förderung rechenschwacher Kinder e.V.
❱24Q4❱ ➜ archive-org-irtberlin-download-Fachwissen-Rechenschwaeche
9 Seiten PDF - Beschreibung/Zusammenfassung, Symptome, Literaturhinweise (längere Ladezeit, da aus archive-org eingebunden)
❱24Q4❱ ➜ kira.dzlm-beispiele-wie-kinder-denken
Wie Kinder denken - Verbreitete Fehlerursachen bei den schriftlichen Rechenverfahren
❱24Q4❱ ➜ rechenschwaeche
PDF-Dateien im Onlinemagazin
❱24Q4❱ ➜ rechenschwaeche
Symptombeschreibung, Fallbeispiele und Literaturliste
❱24Q4❱ ➜ uni-bielefeld-serv-empfehlungen
Thesen und Empfehlungen zum schulischen und außerschulischen Umgang mit Rechenstörungen (pdf) verfasst von Prof. Wilhelm Schipper (Uni Bielefeld) im Auftrag der deutschen Kultusministerkonferenz
❱24Q4❱ ➜ uni-bielefeld-serv-sinus-modul4
MATHEMATIK Lernschwierigkeiten erkennen - verständnisvolles Lernen fördern. Rechenstörungen als schulische Herausforderung (Wilhelm Schipper,2005, 68 S. PDF). Gute Beispiele, wie Eltern und Schüler mit vermeintlichen "Rechentricks" - die jedoch nicht allgemeingültig sind - bei speziellen Aufgabenstellungen zu richtigen Ergebnissen gelangen und so die Kinder verwirren.
❱21Q4❱ ➜ uni-due-de-schriftliche_rechenverfahren_international_2018
Darstellung der Unterschiede in schriftlichen Rechenverfahren verschiedener Herkunftsländer
❱22Q4❱ ➜ verband-dyslexie
Verband Dyslexie Schweiz
❱24Q4❱ ➜ de.wikipedia-wiki-Dyskalkulie
Wikipedia-Artikel: Dyskalkulie
❱24Q4❱ ➜ ztr-rechenschwaeche
Zentrum für Rechenschwäche berlin - mit Forum und Materialien
❱24Q3❱ ➜ ztr-rechenschwaeche-de-service-für-lehrerinnen
Materialien zum Download für Lehrer*innen
Diagnose und Förderbausteine. 8.Auflage 2021
❱24Q3🛒 [Affiliate-Link] ➜ Dyskalkulie - Kindern mit Rechenschwäche wirksam helfen
Kinder fordern uns heraus
Symptomtraining - Kostenlose Arbeitsblätter für das tägliche Mathe-Training zum Download (mehr als 6900 Seiten!)
❱24Q4❱ ➜ bildungsserver.berlin-brandenburg-de-mathematik-praevention_rechenstoerungen-schipper_material_rechenstoerungen.pdf
18 Seiten PDF: Übungen bei Rechenstörungen für Schüler Klasse 1-5
❱24Q4❱ ➜ dyskalkulie-marburg-de-symptome-dyskalkulie-14
Diagnosebogen Dyskalkulie - Symptom-Katalog für Eltern
❱24Q4❱ ➜ icd-code-de-icd-code-F81.2
Dyskalkulie - Definition nach ICD-10: F80-F89 Entwicklungsstörungen / F81.2 Rechenstörung
❱24Q4❱ ➜ legakids-eltern-lehrer-lernmaterialien-kostenlose-uebungen
Seite zum Thema LRS und Rechenschwäche mit kostenlosem Unterrichtsmaterial für die Grundschule
❱23Q2❱ ➜ legasthenie-lvl-bw-de-dyskalkulie-diagnostik
Diagnose einer Dyskalkulie - Wie kann eine Dyskalkulie bei einem Kind festgestellt werden? Info vom Landesvberbans Legasthenie Ba-Wü
Rechenstörungen Theorie und Handreichungen
❱24Q4❱ ➜ arbeitskreis-lernforschungArbeitskreis des Zentrums für angewandte Lernforschung gemeinnützige GmbH Rechenschwäche / Dyskalkulie
❱24Q4❱ ➜ bildungsserver.berlin-brandenburg-de-praevention-rechenstoerungen
Informationen, Materialien und Links zur Prävention von Rechenstörungen
❱24Q4❱ ➜ bildungsserver-seite=794
Linksammlung Rechenschwäche/Dyskalkulie am Dt.Bildungsserver
❱24Q4❱ ➜ opus.bsz-bw-volltexte-2007-16-gerster
Schwierigkeiten beim Erwerb mathematischer Konzepte im Anfangsunterricht - Bericht zum Forschungsprojekt 'Rechenschwäche - Erkennen, Beheben, Vorbeugen' von Hans-Dieter Gerster und Rita Schultz, PH Freiburg, 2000 (427 S. PDF)
❱24Q4❱ ➜ bvl-dyskalkulie
Bundesverband Legasthenie und Dyskalkulie e.V.
❱23Q2❱ ➜ bvl-legasthenie-de-10__Lehrer_Dyskalkulie_2020-pdf
Dyskalkulie in der Schule - 30 Seiten Handreichung vom Bundesverband Legasthenie und Dyskalkulie e.V.
❱24Q4❱ ➜ dimdi-de-dynamic-en-dimdi-for-the-public
Klassifizierung nach ICD-10 der WHO: F81.2
❱24Q4❱ ➜ familienhandbuch-schulprobleme-rechenschwache-grundschuler-ursachen-diagnose-forderung
Prof. Dr. Oliver Thiel: Rechenschwache Grundschüler - Ursachen, Diagnose, Förderung (archive.org)
❱24Q4❱ ➜ ifrk-ev
Initiative zur Förderung rechenschwacher Kinder e.V.
❱24Q4❱ ➜ archive-org-irtberlin-download-Fachwissen-Rechenschwaeche
9 Seiten PDF - Beschreibung/Zusammenfassung, Symptome, Literaturhinweise (längere Ladezeit, da aus archive-org eingebunden)
❱24Q4❱ ➜ kira.dzlm-beispiele-wie-kinder-denken
Wie Kinder denken - Verbreitete Fehlerursachen bei den schriftlichen Rechenverfahren
❱24Q4❱ ➜ rechenschwaeche
PDF-Dateien im Onlinemagazin
❱24Q4❱ ➜ rechenschwaeche
Symptombeschreibung, Fallbeispiele und Literaturliste
❱24Q4❱ ➜ uni-bielefeld-serv-empfehlungen
Thesen und Empfehlungen zum schulischen und außerschulischen Umgang mit Rechenstörungen (pdf) verfasst von Prof. Wilhelm Schipper (Uni Bielefeld) im Auftrag der deutschen Kultusministerkonferenz
❱24Q4❱ ➜ uni-bielefeld-serv-sinus-modul4
MATHEMATIK Lernschwierigkeiten erkennen - verständnisvolles Lernen fördern. Rechenstörungen als schulische Herausforderung (Wilhelm Schipper,2005, 68 S. PDF). Gute Beispiele, wie Eltern und Schüler mit vermeintlichen "Rechentricks" - die jedoch nicht allgemeingültig sind - bei speziellen Aufgabenstellungen zu richtigen Ergebnissen gelangen und so die Kinder verwirren.
❱21Q4❱ ➜ uni-due-de-schriftliche_rechenverfahren_international_2018
Darstellung der Unterschiede in schriftlichen Rechenverfahren verschiedener Herkunftsländer
❱22Q4❱ ➜ verband-dyslexie
Verband Dyslexie Schweiz
❱24Q4❱ ➜ de.wikipedia-wiki-Dyskalkulie
Wikipedia-Artikel: Dyskalkulie
❱24Q4❱ ➜ ztr-rechenschwaeche
Zentrum für Rechenschwäche berlin - mit Forum und Materialien
❱24Q3❱ ➜ ztr-rechenschwaeche-de-service-für-lehrerinnen
Materialien zum Download für Lehrer*innen
Literatur
❱24Q3🛒 [Affiliate-Link] ➜ RechenstörungenDiagnose und Förderbausteine. 8.Auflage 2021
❱24Q3🛒 [Affiliate-Link] ➜ Dyskalkulie - Kindern mit Rechenschwäche wirksam helfen
Kinder fordern uns heraus
Mathematische Modelle - Anschauungsmaterial
➜ Abschnitt ansehen / wegblenden
❱22Q4❱ ➜
stauff-de-modelle-dateien-modelle
Beispiele für Anschauungsmodelle von Kollege Heiner Stauff
Beispiele für Anschauungsmodelle von Kollege Heiner Stauff
Benoten, Bewerten, Kompetenzen
➜ Abschnitt ansehen / wegblenden
➜ siehe auch
Notengebung und Zeugnisse
❱24Q4❱ ➜
schule-bw-de-individuelles-lernen-und-individuelle-foerderung-kompetenzraster-2016-mathematik
Arbeiten mit Kompetenzrastern und Lernwegelisten im Englischunterricht (Landesbildungsserver Ba-Wü) – Klasse 5-10 - mit Handreichungen und Beispielen für Lernmaterialien
Arbeiten mit Kompetenzrastern und Lernwegelisten im Englischunterricht (Landesbildungsserver Ba-Wü) – Klasse 5-10 - mit Handreichungen und Beispielen für Lernmaterialien
Rechenmaschinen und Hilfsmittel
➜ Abschnitt ansehen / wegblenden
❱23Q2❱ ➜
zeno-org-Meyers-1905-A-Rechenmaschinen
Historischer Lexikoneintrag in "Meyers enzyklopädischem Lexikon" von 1905
Historischer Lexikoneintrag in "Meyers enzyklopädischem Lexikon" von 1905
Mein kostenloses Online-Werkstattbuch zu "fast vergessenen" künstlerischen Techniken.
Wie? Gratis?
Ja. Gratis. Lernt 'was Neues!
Kunst trifft Alchemie.

Frohes Stöbern!
180 Seiten online.
Tipps für Tiefdruck, Flachdruck, analoge Fotografie, Cyanotypie, Farbherstellung, Papier schöpfen, Galvanik, Kunstgeschichte ... ein weites Feld ...
Mathematik interaktiv
➜ Abschnitt ansehen / wegblenden
➜ siehe die umfangreiche Sammlung auf Online-Lernprogramme und Apps
Bildungsplan (2016) Ba-Wü
➜ Abschnitt ansehen / wegblenden
❱23Q1❱ ➜
bildungsplaene-bw-de-ALLG-GS-M
Inhalte laut Bildungsplan (2016) für das Fach "Mathematik" GS in Ba-Wü
❱23Q1❱ ➜ bildungsplaene-bw.de-ALLG-SEK1-M
Inhalte laut Bildungsplan (2016) für das Fach "Mathematik" SEK I in Ba-Wü
Inhalte laut Bildungsplan (2016) für das Fach "Mathematik" GS in Ba-Wü
❱23Q1❱ ➜ bildungsplaene-bw.de-ALLG-SEK1-M
Inhalte laut Bildungsplan (2016) für das Fach "Mathematik" SEK I in Ba-Wü
Lehrpläne / Bildungspläne
➜ Abschnitt ansehen / wegblenden
➜ siehe auch
Stoffplan-Formulare und Fachlehrpläne
❱24Q4❱ ➜
kmk-org-lehrplan-datenbank.html
Lehrplandatenbank der Kultusministerkonferenz
❱24Q4❱ ➜ kmk-org-dokumentation-statistik-rechtsvorschriften-uebersicht-lehrplaene
Links zu den Lehrplänen der allgemein bildenden Schulen / Bildungsservern der Bundesländer
❱24Q4❱ ➜ kmk-org-dokumentation-uebersicht-lehrplaene-berufl
Links zu den Lehrplänen der Beruflichen Schulen / Bildungsservern der Bundesländer
❱24Q4❱ ➜ de.wikipedia-Lehrplan
Definition und Linksammlung zu Lehrplänen auf der Wikipedia
Lehrplandatenbank der Kultusministerkonferenz
❱24Q4❱ ➜ kmk-org-dokumentation-statistik-rechtsvorschriften-uebersicht-lehrplaene
Links zu den Lehrplänen der allgemein bildenden Schulen / Bildungsservern der Bundesländer
❱24Q4❱ ➜ kmk-org-dokumentation-uebersicht-lehrplaene-berufl
Links zu den Lehrplänen der Beruflichen Schulen / Bildungsservern der Bundesländer
❱24Q4❱ ➜ de.wikipedia-Lehrplan
Definition und Linksammlung zu Lehrplänen auf der Wikipedia
Bildungspläne der Länder
In den Verzeichnissen sind bei einigen Ländern auch didaktische Handreichungen und Ausarbeitungen zu den Kerncurriculae hinterlegt- Baden-Württemberg
❱21❱ ➜ bildungsplaene-bw.de-BP2016-ALLG
Endfassungen der Bildungspläne 2016 für Baden-Württemberg. Beispielcurricula sind bei den Fachplänen zu finden
❱21❱ ➜ bildungsstandards-bw
Bildungspläne 2004 bis 2015 / Bildungspläne 2016, Download, Niveaukonkretisierungen, Kommentare. Seite des KuMi Ba-Wü - Hier sind die Bildungsstandards, die zum Schuljahr 2004/2008 Als verbindliche Grundlage für die Arbeit der Schulen gültig werden, in ihrer Endfassung veröffentlicht
Außerdem finden sich Links zu den Erprobungsschulen, die Erfahrungsberichte und Material auf ihren Seiten veröffentlicht haben.
❱21❱ ➜ bildungsplaene-bw-de-Lde-4559689
Beispiele für Planungshilfen für Klasse 10 WRS
❱21❱ ➜ schule-bw-unterricht-faecher
In diesem Portal des KuMi Ba-Wü finden Sie Unterrichtsvorschläge und -entwürfe sowie Unterrichts- und Lernmaterialien für verschiedene Fächer aller Schularten, -typen und -stufen - Bayern
❱21❱ ➜ lehrplanplus-bayern-de
Lehrpläne aller Schularten in Bayern - Berlin
❱21❱ ➜ berlin-de-rahmenlehrplaene
Rahmenlehrpläne für Berlin - Brandenburg
❱21❱ ➜ bildungsserver.berlin-brandenburg-rahmenlehrplaene
Rahmenlehrpläne und Materialien für Berlin und Brandenburg - Bremen
❱21❱ ➜ lis.bremen-de-bremen56.c.15219
Rahmenlehrpläne für Bremen am Landesinstitut für Schule - Hamburg
❱21❱ ➜ hamburg-de-bildungsplaene
Bildungspläne für Hamburg - Hessen
❱21❱ ➜ kultusministerium-hessen-Kerncurricula-und-Lehrplaene
Bildungspläne, Bildungsstandards und Kerncurriculae - Mecklenburg-Vorpommern
❱25Q1❱ ➜ bildung-mv-unterricht-rahmenplaene
Bildungspläne Mecklenburg-Vorpommern - Niedersachsen
❱21❱ ➜ bildungsportal-niedersachsen-de-allgemeinbildung-vorgaben
Bildungspläne, Bildungsstandards und Kerncurriculae - Nordrhein-Westfalen
❱21❱ ➜ schulentwicklung-nrw-de-lehrplaene
Lehrplannavigator für NRW - Rheinland-Pfalz
❱21❱ ➜ lehrplaene-bildung-rp-de
Lehr- und Rahmenpläne - Saarland
❱21❱ ➜ saarland-de-lehrplaenehandreichungen
Lehrpläne und Handreichungen - Sachsen
❱21❱ ➜ schulportal-sachsen-de-lplandb
Lehrplandatenbank - Sachsen-Anhalt
❱21❱ ➜ lisa-sachsen-anhalt-lehrplaenerahmenrichtlinien
Lehrpläne und Rahmenrichtlinien - Schleswig-Holstein
❱24Q2❱ ➜ fachportal-lernnetz-de-sh-fachanforderungen
Lehrpläne des Landes Schleswig-Holstein - Thüringen
❱21❱ ➜ schulportal-thueringen-lehrplaene
Lehrpläne der allgemein bildenden und der Berufsbildenden Schulen
Neue und alte Techniken der Radierung und Edeldruckverfahren
Vom Hexenmehl und Drachenblut zur Fotopolymerschicht - ein Werkstattbuch
Tipps, Tricks, Anleitungen, Verfahren und Rezepturen aus 5 Jahrhunderten -
erlesen, erfahren, erfunden und gesammelt von Wolfgang Autenrieth
erlesen, erfahren, erfunden und gesammelt von Wolfgang Autenrieth
Nochmals erweiterte 7. Auflage, ISBN 978-3-9821765-0-5, zweispaltig im Großformat, 232 Seiten - 36,90 € zzgl. Versand
➥ Wege zum Buch
Zum Reinschnuppern: Das kostenlose ➜
"Alchemistische Online-Werkstattbuchversion" mit 180 Teilkapiteln


