Themen I
Besondere Zahlen Durchschnitt Fibonacci-Zahlen Formeln + Onlinerechner Gewichte historisch Geschwindigkeit Hexeneinmaleins Goldener Schnitt Länge und WellenlängeThemen II
Längenmaße historisch Längenmaße international LOVE - die Weltformel Magische Quadrate etc. "Magische" Zahlen Pi - die magische Zahl Pi - Herleitung Pi + Kreis Pi + KreisflächeThemen III
Pi + Kreissegmente Pi + Kreisumfang Pi + Kugeloberfläche Pi + Zylindervolumen "Pi-zza-Theorem" Potenzen Primzahlen Prozente + Verhältnisse RechentricksThemen IV
Spiralen + Schnecken Teilbarkeitsregeln Volumenberechnung Wahrscheinlichkeit+Lotto Zahlen (große) Zahlen (ganz kleine) Zahlenfolgen Zahlenräume Zahlvorstellung ZahlenmystikThemen V
Bündelungen Zeit messen + darstellen Asche der Menschheit Atemluft-Aufgabe 1: Auto Atemluft-Aufgabe 2: Bäume Benzin am Alpenrand Fermi-Aufgaben Filme zum Matheunterricht Links zu Fermi-AufgabenThemen VI
Menschen im Bodensee Nachkommen von Kaiser Karl Mauer USA - Mexiko Obertor von Isny Rechenmaschinen Sind wir unsterblich? Silvesterballerei Sind wir eigentlich da? Volumen der Menschheit
Abbildung gemeinfrei. Quelle: https://de.wikipedia.org/wiki/Pi-Tag#/media/Datei:Pi_pie2.jpg
Mathematik - Linktipps, Filme + Literatur
➜ Abschnitt ansehen / wegblenden
❱24Q3❱ ➜
mathematikalpha-de-mathematikbuecher
Digitalisierte Mathematik-Lehrbücher der ehemal. DDR und aus Russland.
❱24Q3❱ ➜ mathematikalpha-schuelerbuecherei
Digitalisierte historische Mathematikbücher
❱21❱ ➜ mathematikalpha-lvz-mathematikhefte
Ebenfalls auf dieser Webseite zu finden sind Beilagen der Leipziger Volkszeitung. Ein Fundus für Matheaufgaben mit witzigen Illustrationen.
❱21❱ ➜ num-math-uni-goettingen-schmankerl-pdf
358 Seiten PDF online mit Beispielen für "Merkwürdige Mathematik"
❱21❱ ➜ wispor-wpx-mat1
Interessantes aus der Mathematik: Römische Zahlen, Zahlentheorie, Pi, vollkommene Zahlen, Lotto, Witziges, Mathematische Quadrate ...
Bayrischern Rundfunk: Suchergebnis nach Mathematik-Sendungen
❱21❱ youtube-com-watch?v=f6UMdo81A1g
youtube: Mathematik zum Anfassen - Playlist
❱21❱ youtube-com-watch?v=5NG-msbuBM4
Mathematik zum Anfassen! - Festvortrag Albrecht Beutelspacher, Direktor des Mathematikums in Gießen. Dodekaeder, Fußbälle, eine Pyramide aus einem Blatt falten (ohne zu schneiden)-und was das mit Tetrapack zu tun hat, Rechentricks bei der Multiplikation großer Zahlen, vedische Multiplikation, die Quadratur des Kreises,
❱21❱ arte-das-geheimnis-der-mathematik
Eine faszinierende Reise durch die Welt der Mathematik, von Pythagoras über Newton bis hin zu Einstein. 53'
Fibonacci-Zahlen, Pi, Platonische Körper, Fallgeschwindigkeit, Newtonsche Gesetze (Gravitation), elektromagnetische Wellen, Teilchenphysik
Digitalisierte Mathematik-Lehrbücher der ehemal. DDR und aus Russland.
❱24Q3❱ ➜ mathematikalpha-schuelerbuecherei
Digitalisierte historische Mathematikbücher
❱21❱ ➜ mathematikalpha-lvz-mathematikhefte
Ebenfalls auf dieser Webseite zu finden sind Beilagen der Leipziger Volkszeitung. Ein Fundus für Matheaufgaben mit witzigen Illustrationen.
❱21❱ ➜ num-math-uni-goettingen-schmankerl-pdf
358 Seiten PDF online mit Beispielen für "Merkwürdige Mathematik"
❱21❱ ➜ wispor-wpx-mat1
Interessantes aus der Mathematik: Römische Zahlen, Zahlentheorie, Pi, vollkommene Zahlen, Lotto, Witziges, Mathematische Quadrate ...
Filme zum Matheunterricht
❱21❱ br-de-service-suche-query=MathematikBayrischern Rundfunk: Suchergebnis nach Mathematik-Sendungen
❱21❱ youtube-com-watch?v=f6UMdo81A1g
youtube: Mathematik zum Anfassen - Playlist
❱21❱ youtube-com-watch?v=5NG-msbuBM4
Mathematik zum Anfassen! - Festvortrag Albrecht Beutelspacher, Direktor des Mathematikums in Gießen. Dodekaeder, Fußbälle, eine Pyramide aus einem Blatt falten (ohne zu schneiden)-und was das mit Tetrapack zu tun hat, Rechentricks bei der Multiplikation großer Zahlen, vedische Multiplikation, die Quadratur des Kreises,
❱21❱ arte-das-geheimnis-der-mathematik
Eine faszinierende Reise durch die Welt der Mathematik, von Pythagoras über Newton bis hin zu Einstein. 53'
Fibonacci-Zahlen, Pi, Platonische Körper, Fallgeschwindigkeit, Newtonsche Gesetze (Gravitation), elektromagnetische Wellen, Teilchenphysik
Teilbarkeitsregeln
Kopfrechnen und Rechentricks➜ Abschnitt ansehen / wegblenden
- Teilbarkeit durch 2: Eine Zahl ist durch 2 ohne Rest teilbar, wenn in der letzten Stelle (der Einerstelle) eine gerade Zahl steht, also eine 0, 2, 4, 6 oder 8
- Teilbarkeit durch 3:
Eine Zahl ist durch 3 ohne Rest teilbar, wenn ihre Quersumme durch 3 ohne Rest teilbar ist
648: Quersumme ist 18; 18 ist ohne Rest durch 3 teilbar - Teilbarkeit durch 4:
Eine Zahl ist durch 4 ohne Rest teilbar, wenn die Zahl aus den letzten beiden Ziffern ohne Rest durch 4 teilbar ist
1528: letzten Stellen -- 28 ist durch 4 teilbar - Teilbarkeit durch 5: Eine Zahl ist durch 5 ohne Rest teilbar, wenn die letzte Ziffer eine 0 oder eine 5 ist
- Teilbarkeit durch 6: Eine Zahl ist durch 6 ohne Rest teilbar, wenn die letzte Ziffer eine gerade Zahl und die Quersumme ohne Rest durch 3 teilbar ist
- Teilbarkeit durch 6: Eine Zahl ist durch 6 teilbar, wenn sie durch 2 und 3 teilbar ist
- Teilbarkeit durch 7:
Eine Zahl ist durch 7 teilbar, wenn ihre letzten zwei Ziffern plus 2 mal alle Ziffern davor durch 7 teilbar sind
322 --- 22 + 2x3 = 28, also durch 7 teilbar
4786908 --- 8 + 2x47869 = 8 + 95738 = 95746
nochmal: 95746 --- 46 + 2x957 = 46+1914 = 1960
nochmal: 1960 --- 60 + 38 = 70 + 28, also durch 7 teilbar - Teilbarkeit durch 7:
Eine Zahl ist durch 7 teilbar, wenn das Ergebnis der Differenz aus dem Doppelten der letzten Ziffer vom vorderen Zahlenrest durch 7 teilbar ist:
322 --- 32-2x2 = 28, also teilbar
413 --- 41-2x3 = 35, also teilbar
mehrstufig:
67018
6701-16=6685
668-10=658
65-16=49 , also durch 7 teilbar - Teilbarkeit durch 8: Eine Zahl ist durch 8 ohne Rest teilbar, wenn die die Zahl aus den letzten drei Ziffern dieser Zahl ohne Rest durch 8 teilbar ist
- Teilbarkeit durch 8: Ist die Hälfte der Zahl durch 4 Teilbar, so ist die ursprüngliche Zahl durch 8 Teilbar
- Teilbarkeit durch 9: Eine Zahl ist durch 9 ohne Rest teilbar, wenn ihre Quersumme ohne Rest durch 9 teilbar ist
- Teilbarkeit durch 10: Eine Zahl ist durch 10 teilbar, wenn ihre letzte Ziffer eine 0 ist
- Teilbarkeit durch 11:
Eine Zahl ist durch 11 teilbar, wenn ihre alternierende Quersumme durch 11 teilbar oder 0 ist
61259 --- alternierende Quersumme: 6 - 1 + 2 - 5 + 9 = 11 => durch 11 Teilbar (5569*11=61259) - Teilbarkeit durch 11 (für Zahlen >100):
Eine Zahl ist durch 11 teilbar, wenn die Differenz der beiden vorletzten Ziffern mit der letzten Ziffer 11 ergibt
61259 --- 259 --- 25-9=11 => durch 11 Teilbar - Teilbarkeit durch 12: Eine Zahl ist durch 12 ohne Rest teilbar, wenn sie durch 3 und durch 4 ohne Rest teilbar ist (Grund 3x4=12)
- Teilbarkeit durch 13 (für Zahlen >1001:
Eine natürliche Zahl ist genau dann durch 13 teilbar, wenn ihre alternierende 3er-Quersumme durch 13 teilbar ist
19149 --- 149-19=130, also teilbar
629174 --- 174-629 = -455 = 390 + 65 = 30x13 + 5x13, also teilbar - Teilbarkeit durch 14: Zahl halbieren, danach das Verfahren zur Überprüfung der Teilbarkeit durch 7 verwenden
- Teilbarkeit durch 15: Eine Zahl ist durch 15 ohne Rest teilbar, wenn sie durch 3 und durch 5 ohne Rest teilbar ist
- Teilbarkeit durch 16: Eine Zahl ist durch 16 teilbar, wenn die letzten vier Stellen durch 16 teilbar sind.
- Teilbarkeit durch 17:
Eine Zahl ist durch 17 teilbar, wenn man fortgesetzt das Fünffache der letzten Ziffer von den verbleibenden abziehen kann
11101 --- 1110-5=1105
1105 --- 110-25=85
85 ist durch 17 teilbar, denn 2x85=170, also ist auch 11101 durch 17 teilbar. - Teilbarkeit durch 18: Eine Zahl ist durch 18 ohne Rest teilbar, wenn sie durch 2 und durch 9 ohne Rest teilbar ist
- Teilbarkeit durch 20: Eine Zahl ist durch 20 ohne Rest teilbar, wenn ihre letzte Stelle eine 0 und ihre vorletzte Stelle gerade ist
- Teilbarkeit durch 24: Eine Zahl ist durch 24 ohne Rest teilbar, wenn sie durch 3 und durch 8 teilbar ist (siehe oben)
- Teilbarkeit durch 25: Eine Zahl ist durch 25 ohne Rest teilbar, wenn die letzten beiden Ziffern durch 25 teilbar sind, also 00, 25, 50 oder 75 lauten
- Teilbarkeit durch 33: Eine Zahl ist durch 33 ohne Rest teilbar, wenn sie durch 3 und durch 11 teilbar ist (siehe oben)
- Teilbarkeit durch Zweierpotenzen 2n: Eine Zahl ist durch 2n (=16, 32, 64, ...) ohne Rest teilbar, wenn die letzten n Ziffern der Zahl durch 2n teilbar sind.
Rechentricks
➜ Abschnitt ansehen / wegblenden
Schnellrechentricks - Sammlungen
❱21❱ ➜ archive-org-mathforum.org-mathtips-beatcalcSchnellrechentricks: Quadratzahlen, multiplizieren, addieren, subtrahieren, dividieren, Prozentrechnen
❱21❱ ➜ de-wikipedia-org-wiki-Chisanbop
Koreanische Fingerrechenmethode, mit der man grundlegende arithmetische Operationen wie Zählen oder die Grundrechenarten ausführen kann. Sie ähnelt dem Rechnen mit dem Abakus
Addition / Subtraktion
❱21❱ ➜ cut-the-knot-arithmetic-LongSumLange Reihe ähnlicher Zahlen addieren (Mittelwertprinzip)
❱21❱ ➜ youtube--aVFIlhyxfJw
Es handelt sich um "mentales Rechnen" indisches Fingerrechen. Die Schüler stellen sich einen indischen Abakus vor, den sie mit den Fingern abbilden. Dazu werden jedoch beide Hände benutzt.
Multiplikation / Vielfache
❱21❱ ➜ youtube--2iowDMbA7x8Multiplikation der Neunerreihe mit den Fingern
❱21❱ ➜ tinohempel-info-mathe-finger
Multiplikation der Zahlen 5 bis 9 mit den Fingern
❱21❱ ➜ youtube--yHF95qXx8GQ
Vedisches Rechnen: Multiplikation von Zahlen, die nahe 100 liegen
Japanische Linienmultiplikation
❱21❱ ➜ youtube--t_u0_9SzYE0Japanische Linienmultiplikation
❱21❱ ➜ youtube--DCqOrrQpH0s
Japanische Linienmultiplikation (Duden, durch Werbung unterbrochen)
Multiplikationstabellen
❱21❱ ➜ vielfache_muster.xlsExcel-Tabelle zum Download: Zahlenreihen / Multiplikationstabelle gefärbt
Wurzel ziehen
❱21❱ ➜ tinohempel-info-mathe-wurzelWurzelziehen von Hand
Einfache Rechenmaschinen - nach Adam Riese
siehe auch ➜ EDV-Geschichte❱21❱ ➜ tinohempel-info-mathe-ries
Rechnen mit dem Rechenbrett von Adam Ries
❱21❱ ➜ tinohempel-info-mathe-napier
Division und Multiplikation mit der Rechenmaschine / dem Rechenverfahren von John Napier
Formeln, Onlinerechner + Formelspielereien
➜ Abschnitt ansehen / wegblenden
Merksätze
❱21❱➜ siehe auch de.wikipedia-org-Liste_von_Merksprüchen#MathematikMerksprüche für Formeln und mathematische Konstanten
Onlinerechner / Online-Graphenplotter
❱21❱ ➜ rechneronline-de/Onlinerechner für fast alles, Online-Funktionsplotter
❱21❱ ➜ mathe-fa.de/de
Onlinerechner für fast alles, Online-Funktionsplotter
❱21❱ ➜ mathsisfun-com-grapher-equation
Funktionsplotter für viele Formeln. Die Formel kann direkt eingegeben werden.
❱21❱ ➜ rechneronline-de-glossar
Onlinerechner- Glossar der verschiedenen Rechner
Die Weltformel
All you need is lovey=1/x
x2+y2= 9
y=abs(-2x)-3.5
x=-abs(3sin(0.8y))
:-)




erstellt mit mathsisfun.com-data-grapher-equation
Kreis und Pi - Was ist Pi?
➜ Abschnitt ansehen / wegblenden
Pi-Tag
Der Pi-Day wird am 14.März gefeiert, exakt beginnt er um 1 Uhr 59 nachmittags. Der Grund? Im anglo-amerikanischen Raum wird der Monat vor dem Tag genannt. Zudem kann man nachmittags besser anstoßen als nachts um 2 Uhr.Darstellung von Pi als Datum im angloamerikanischen System:
3-14 1:59 26,53"
Damit sind die ersten 9 Nachkommastellen genannt.
Wie lange es noch bis zum Pi-Day dauert, lässt sich mit dieser Website berechnen:
➜ yourcountdown-to-pi-day
Weil π im Englischen als /paɪ/ ausgesprochen wird, backen (manche) Mathematiker an diesem Tag Kuchen (engl. "pie").
Als Begründer dieser Tradition gilt Larry Shaw, der den Pi-Day 1988 am Exploratorium in San Francisco initiierte, wo er seitdem jährlich begangen wird.

Pi-Pie (ein π-Kuchen mit π gerundet auf 27 Nachkommastellen), hergestellt an der Technischen Universität Delft
Abbildung gemeinfrei. Quelle: https://de.wikipedia.org/wiki/Pi-Tag#/media/Datei:Pi_pie2.jpg
Hier findet sich ein Rezept für einen originalen Pie zum Download: ➜ kinder-wdr-de-tv-wissen-macht-ah-bibliothek-am-gaumen-100
Der Pi-Annäherungstag, welcher auch Pi Approximation Day genannt wird, wird am 22. Juli gefeiert. Es wird die näherungsweise Darstellung von π durch Archimedes als 22/7 ≈ 3,14 geehrt.
Am 12.März 2009 hat das amerikanische Repräsentantenhaus mit der Resolution 111 H. Res. 224 den 14.März zum "Nationalen Pi-Tag" erklärt.
Kann es Zufall sein, dass einer der brilliantesten Köpfe der Physik und Mathematik, ➜ Albert Einstein, am Pi-Day geboren wurde?
Ein weiterer bedeutender Mathematiker, der am 14. März geboren wurde, ist ➜ Wacław Sierpiński. Er wurde bekannt für seine Arbeiten in der Mengenlehre und der Topologie.
Auch ➜ Paul Ehrlich, Arzt, Forscher und Nobelpreisträger, der für seine Arbeiten in der Immunologie und Chemotherapie bekannt ist, hatte an diesem Tag Geburtstag. Er entwickelte auch das erste Antibiotikum, sowie Zellfärbemethoden mit Methylenblau, die zentral für die Zellforschung wurden
'Philosophische' Vorbemerkung
Pi besitzt unendlich viele Nachkommastellen. Dies beinhaltet, dass jede mögliche - nicht-periodische, nicht-unendliche - Zahlenfolge an irgendeiner Stelle in Pi auftaucht.Liest man die Zahlenfolgen in Pi als Codes für Ascii-Zeichen, so taucht in Pi der Name jeder Person, jeder Stadt, jedes Gegenstandes in jeder Sprache des Universums auf. Ebenso das Geburts- und Todesdatum jeder Person, die jemals lebte oder leben wird. Konvertiert man einen Ausschnitt der Zahlenfolge in eine Bitmap, wird diese das erste zeigen, was du gesehen hast und das letzte, das du sehen wirst. Ebenso wie das Bild jeden Moments, der zwischen diesen beiden Ereignissen gesehen wurde. Jede Information, die jemals existierte - ebenso wie die DNA-Information jeden Lebewesens - ist in PI enthalten. ALLES ist enthalten im Quotienten aus Umfang und Durchmesser eines Kreises.
The circle of life.
➜ angio-net-pi-piquery-html
Auf dieser Internetseite lässt sich Pi nach Zahlenfolgen durchsuchen. Gibt man z.B. als Geburtstag den 23.05.1986 als 23051986 ein, erhält man als Antwort:
"The string 23051986 occurs at position 8321243. This string occurs 2 times in the first 200M digits of Pi."
Näherungswerte von Pi
- π = 3.141592653589793238462643383279502884197169399375105820974944592... ad infinitum
- Plato (427-348 v.Chr.) gab als Näherungswert für Pi √2 + √3 = 3.146 an.
- Bereits in Babylon hatte man für Pi die Näherung 3⅛ gefunden, was als Dezimalbruch 3,125 ergibt.
- Im alten Ägypten war der Wert 3,16049 bekannt
- Im alten Indien galt 3,08832
- Den Chinesen wird der mögliche Wert 3,16227 zugeschrieben
- Näherungsbruch mit 6 Nachkommastellen: pi ~ 355 / 113 = 3,141592...
- Ein Näherungswert ist 22⁄7 = 3,142857143
- 1706 berechnete John Machin aus der Arcustangens Reihe unter Zuhilfenahme des Additionstheorems eine Folge, aus der sich die ersten hundert Nachkommastellen ergeben:
π/4 = 4 arctan 1 / 5 - arctan 1 / 239 - sin1 /5555555°=3,1415927·10–10(siehe dazu den ➜ Artikel in Spektrum d. Wissenschadft)
- Leibniz-Reihe für π
$$
\frac{\pi}{4} = \sum_{k=0}^{\infty} \frac{(-1)^k}{2k + 1} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \dots
$$ - Machin-Formel für π
$$
\frac{\pi}{4} = 4 \arctan \left(\frac{1}{5}\right) - \arctan \left(\frac{1}{239}\right)
$$ - BBP-Formel (Formeln zur Extraktion von Ziffern)
Die Bailey-Borwein-Plouffe (BBP)-Formel ist revolutionär, da sie es ermöglicht, die n-te Ziffer von π im Hexadezimal- oder Binärsystem zu berechnen, ohne die vorhergehenden n−1 Ziffern berechnen zu müssen.
$$
\pi = \sum_{k=0}^{\infty} \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6} \right)
$$ - Ramanujan-Formel für π
$$
\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{k=0}^{\infty} \frac{(4k)!(1103 + 26390k)}{(k!)^4 396^{4k}}
$$
Die Ramanujan-Formel für π konvergiert extrem schnell.
Jeder Term (k) der unendlichen Summe erhöht die Anzahl der exakt berechneten Nachkommastellen von π um etwa 8 Dezimalstellen.
Der erste Term (k=0): Bereits das Aufsummieren des ersten Terms (für k=0) ergibt eine Annäherung, die π auf 8 Nachkommastellen genau wiedergibt.
Der zweite Term (k=1): Das Hinzufügen des zweiten Terms (für k=1) erhöht die Genauigkeit auf etwa 16 Nachkommastellen (8 + 8).
Der dritte Term (k=2): Nach drei Termen (k=0,1,2) erreicht man eine Genauigkeit von etwa 24 Nachkommastellen. - Chudnovsky-Formel für π
$$
\frac{1}{\pi} = 12 \sum_{k=0}^{\infty} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 (640320)^{3k + 3/2}}
$$
Diese Formel ist eine Weiterentwicklung der Ramanujan-Reihen und liefert etwa 14 bis 15 neue korrekte Dezimalstellen pro Term (k). Sie war die Grundlage für viele Weltrekordberechnungen von π.
Pi in Zahlenreihen
- Die Zahl Pi hängt auf folgende Art mit den ungeraden Zahlen zusammen:
π/4 = 1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 … - Pi als Bruchstufenzahl:

im Nenner stehen die Quadratzahlen von 3,5,7,9,11,... - Das "Basler Problem" war lange Zeit ungelöst, bis Euler die Lösung fand. Er wies nach, dass 1 + 1/4 + 1/9 + 1/16 + 1/25 + .... gegen π2/6 strebt.
Der Autor dieses Beitrages verwendet zum Nachweis einen Trick, der über die Abnahme der Lichtstärke geht - denn diese nimmt im Quadrat zur Entfernung ab.
siehe auch ➜ youtube-v=d-o3eB9sfls
siehe auch ➜ youtube-v=CTYuVXNaFlk, hier wird es über eine ➜ Taylorreihe dargestellt - π/2 = 2/1*2/3*4/3*4/5*6/5*6/7*..... das sog. Wallis'sche Produkt. Es wurde 1655 von dem englischen Mathematiker John Wallis entdeckt. Die Zahlenreihe ist zur Berechnung von Pi nicht sonderlich geeignet, da die Konvergenz erst nach ca. 1 Mio Termen eine Annäherung an Pi ergibt.
An der "Uni. Rochester (USA) wurde 2015 eine Anwendung dieses Produkts bei der Berechnung des Fehlers der quantenmechanischen Variationsrechnung der Energieeigenzustände im angeregten Wasserstoffatom relativ zur Lösung im Bohr’schen Atommodell entdeckt."(a.a.O.)
Pi-faktisch
- Der Rekord der Berechnung von Pi lag im August 2021 bei 62,8 Billionen Stellen hinter dem Komma
- Der Inder Suresh Kumar Sharma ist Weltrekordhalter im Memorieren von Pi mit 70.030 Nachkommastellen, die er am 21. Oktober 2015 fehlerfrei und auswendig in einer Zeit von 17 Stunden und 14 Minuten aufsagte.
- π = 3·100 + 1·10-1 + 4·10-2 + 1·10-3 + 5·10-4 + 9·10-5 + 2·10-6 + 6·10-7 + 5·10-8 + 3·10-9 ...
- Die erste Million Nachkommastellen von π enthält recht gleichmäßig verteilt 99.959 Nullen, 99.758 Einsen, 100.026 Zweier, 100.229 Dreier, 100.230 Vierer, 100.359 Fünfer, 99.548 Sechser, 99.800 Siebener, 99.985 Achter und 100.106 Neuner (Arndt, Jörg and Christoph Haenel. Pi Unleashed. Trans. Catriona and David Lischka. New York, NY: Springer-Verlag Berlin Heidelberg, 2001)
- Pi ist die erste positive Nullstelle der Sinus-Funktion, somit ist Pi in so gut wie allen Rechnungen, die mit Schwingungen zu tun haben, enthalten - auch in der Musik.
- In der Star-Trek-Episode “Wolf in the Fold,” bringt Spock den feindlichen Computer zum Absturz, indem er diesen anweist, die letzte Nachkommastelle von Pi zu errechnen.
- Für Zahlenmystiker:
Die Summe der ersten 144 Nachkommastellen von π ergibt 666 - die "Satanszahl" und dabei ist auch noch 144 = (6+6) x (6+6). Zum Teufel aber auch! - Noch etwas für Zahlenmystiker:
Ein Kreis hat 360 Grad. π hängt direkt mit dem Kreis zusammen - ab der 359. Stelle von π erscheint die Ziffernfolge 3-6-0. - Ganz besonders mystisch ist Riemanns Paradoxon:
π = ∞ - ∞
Pi ist unendlich-unendlich
BTW: Es wurde wohl nicht von Riemann postuliert, sondern beruht auf dem "Riemannschen Umordnungssatz" - wie in Spektrum der Wissenschaft erläutert wird.
❱21❱ siehe auch ➜ hier auf youtube erklärt (auf englisch) - In diesem Zusammenhang darf auch Leonhard Euler nicht fehlen, er wies nach, dass
eπi +1 = 0 ist.
Eulersche Identität, auch dargestellt als eπi = -1 - Kommt das Ende von π?
"Der amerikanische Mathematiker Robert Palais schlug 2001 in einer Ausgabe des Mathematik-Magazins „The Mathematical Intelligencer“ vor, für π, statt wie bisher den Quotienten aus Umfang und Durchmesser eines Kreises, in Zukunft den Quotienten aus Umfang und Radius (entsprechend 2 π ) als grundlegende Konstante zu verwenden. Seine Argumentation beruht darauf, dass in vielen mathematischen Formeln der Faktor 2 vor der Kreiszahl auftauche. Ein weiteres Argument ist die Tatsache, dass die neue Konstante im Bogenmaß einen Vollwinkel darstellt, statt wie π einen halben Winkel, und so weniger willkürlich wirkt. Die neu normierte Kreiszahl, für deren Notation Michael Hartl und Peter Harremoës den griechischen Buchstaben τ (Tau) vorschlugen, würde diese Formeln verkürzen.
❱21❱ siehe auch ➜ Wikipedia - Wie viel ist pi^pi ^ pi^pi?
Nein, nicht Pipi hoch Pipi in Form von Urin oder Langstrumpf, sondern als Zahl, geschrieben als pi pi pi pi
2222 = 224 = 216 = 65536 ... das ist noch überschaubar. Geschrieben wird das auch 2↑↑4 Doch dann wächst das expotentiell (Wer hätte das gedacht...)
3333 = 3327 ≈37,6 × 1012, das sind schon 3 hoch 7.6 Trillionen oder einfach 3↑↑4
π↑↑4 ist dann bereits π1,3 Quintillionen ... - Beschießt man ein Quadrat mit der Seitenlänge 2 mit zufällig auftreffenden Punkten, dann verteilen diese sich nach dem Gesetz der großen Zahlen recht gleichlmäßig über die gesamte Fläche. Legt man in dieses Quadrat einen Einheitskreis und zählt die Treffer darin, so ist das Verhältnis der Treffer im Kreis zu allen Treffern näherungsweise gleich dem Verhältnis von pi zur Zahl 4. (Fläche des Einheitskreises durch Quadratfläche).
Quelle: "Näherung von Pi mit der Monte-Carlo-Methode" - dort mit Abb.: ➜ schule-bw-de-mathematik-unterrichtsmaterialien-zahl-pi - Sucht man in der Zahl π nach der Antwort auf alle Fragen - der Zahl 42 - ist das unspektakulär. Sie erscheint an Position 92. Die Zahl 42424242 erscheint jedoch an Position 242422, nimmt man die 3 und den Punkt dazu, ist es Position 242424
- Richard Feynman, ein Physiker, wollte die ersten 762 Nachkommastellen der Kreiszahl auswendig lernen. Ab der 763.Stelle folgen sechs aufeinanderfolgende Neunen. Er wollte dann mit "… 999999 und so weiter" enden und daher wird diese Stelle in π nun "Feynman-Punkt" genannt.
- Die Fläche des Inkreises eines pythagoreischen Dreiecks mit den Seitenlängen 3-4-5 beträgt π2
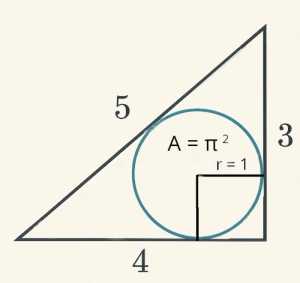
Grafik: Erstellt von W.Autenrieth 2025, CC1.0, Public Domain
Merksätze für π
- Mein Lieblings-Merksatz für die ersten 9 Nachkommastellen von Pi: "May I have a large container of coffee?" "Thank you!"
(Man zähle die Buchstaben der Worte...) - How I want a drink - alcoholic of course - after the heavy lectures involving quantum mechanics
- Wie, o dies π
macht ernstlich so viele Müh’.
Lernt immerhin, Jünglinge, leichte Verselein,
Wie so zum Beispiel dies dürfte zu merken sein! - Now I, even I, would celebrate
In rhymes inapt, the great
Immortal Syracusan, rivaled nevermore,
Who in his wondrous lore,
Passed on before
Left men his guidance
How to circles mensurate. - Für die ersten 31 Nachkommastellen von Pi:
"Now I will a rhyme construct,
By chosen words the young instruct.
Cunningly devised endeavour,
Con it and remember ever.
Widths in circle here you see,
Sketched out in strange obscurity."
Quelle ❱21❱ ➜ nrich-maths-org-2490 - Für die ersten 740 Nachkommastellen von Pi gibt es ein Gedicht von Michael Keith. Er hat dazu die Ballade von Edgar Allen Poe 'The Raven' (Der Rabe) modifiziert:
siehe auch ❱21❱ ➜ cadaeic-net-naraven-htm - Für 740 Stellen existiert das Gedicht von Mike Keith, das er an "Near a Raven" von E.A.Poe anlehnt:
➜ www.cadaeic.net-naraven.htm - 4000 Stellen enthält "Cadeic Cadenza vom selben Autor - wobei die erstn 740 Stellen o.a. "Near a raven" darstellen:
➜ www.cadaeic.net-cadenza.htm

Linktipps
❱21❱ ➜ 3.141592653589793238462643383279502884197169399375105820974944592-eu/Die Zahl Pi als Webadresse und mit Infos zur Faszination in Ziffern
❱21❱ ➜ 3.141592653589793238462643383279502884197169399375105820974944592.eu/wp-content/uploads/2020/03/pi-314-inhalt.pdf
Gerald Steffens hat sein Buch zu π nun als PD veröffentlicht. Das Buch hat einen Umfang von 204 Seiten und enthält - π. Genauer: Die ersten 1 Mio Nachkommastellen. ;-)
❱24Q4❱ ➜ erlebnisland-mathematik-de-vertiefungstext-die-kreiszahl
Erklärungstext zu Pi mit Vorstellung verschioedener Formeln für die ermittlung von Näherungswerten
❱21❱ ➜ mathshistory.st-andrews-HistTopics-Pi_chronology
Historische Übersicht zu Berechnungen der Zahl Pi
❱21❱ ➜ joyofpi-com-pilinks
Webseiten zur Zahl Pi (engl.)
❱21❱ ➜ logisch-gedacht-de-pi-berechnen-lambert-kettenbruch-c
C-Programm (Code) zur Berechnung von Pi
❱23Q4❱ ➜ pi2e-ch-blog-2017-pi-digits-download
Hier können bis zu einer Trillion Nachkommastellen heruntergeladen werden.
❱23Q4❱ ➜ pi2e-ch-wp-content-2017-pi_dec_1m-txt
1 Million Nachkommastellen als Textdatei
❱21❱ ➜ pi314-at
Freunde der Zahl Pi - mit vielen Querverweisen
❱21❱ ➜ quora-Why-is-Pi-regarded-as-such-an-important-number-in-mathematics
Weshalb ist pi eine faszinierende Zahl? Tipp am Rande: Wenn man innerhalb von Quora einen weiter führenden Link anklickt, kommt ein Anmeldeschirm. Der lässt sich umgehen, wenn man den Mauszeiger in die Browser-Linkzeile setzt und "Enter" drückt ;-)
❱21❱ ➜ tetraktys-de-zahlentheorie-9-Kreiszahl
Hier wird auf einen interessanten Zusammenhang zwischen der Kreiszahl Pi und n-Ecken bzw. Simplexen hingewiesen
Wikipedia
❱21❱ ➜ de-wikipedia-org-Pi-TagWikipedia: Pi-Day
❱21❱ ➜ en-wikipedia-org-Pi_Day
Wikipedia: Pi-Day
❱21❱ ➜ de-wikipedia-org-Pi-Sport BTW: Der Weltrekord im Memorieren von π liegt derzeit (2021) bei 70.030 Stellen - fehlerfrei aufgesagt von Suresh Kumar Sharma am 21. Oktober 2015
❱21❱ ➜ de-wikipedia-org-Pi
Wikipedia: π (englische Ausgabe)
❱21❱ ➜ en-wikipedia-org-Pi
Wikipedia: π (englische Ausgabe)
Filme und Töne
❱21❱ ➜ youtube-com-watch?v=W8RE2NyAiJgKate Bush besingt die Zahl Pi - das Video ist dabei grafisch nett animiert und Kate zeigt und besingt die Nachkommastellen von Pi auf 120 Stellen genau. "Kate Bush sollte indes noch einmal in sich gehen, bevor sie sich bei einem Pi-Fanklub bewirbt. In ihrem Lied ist schon die vierundfünfzigste Nachkommastelle falsch; und irgendwann später fehlen unvermittelt 22 Stellen der Zahl Pi.(https://www.welt.de/print-welt/article200608/Wissenschaft-Geheimnisse-der-Zahl-Pi.html)".
❱21❱ ➜ youtube-com-watch?v=FJwzsSPkuWQ
youtube: Mathematik zum Anfassen - Die Zahl Pi (1. Staffel, 3. Folge) Mit einigen Herleitungen und Beispielen zu Aproximationen
❱23Q4❱ ➜ https://www.youtube.com/watch?v=HV1-AjwDJwM
Die Zahl pi musikalisch aufgeschlüsselt. In Dreiergruppen definiert die erste Zahl die Note in einer pentatonischen Reihe, die zweite Zahl die Dauer und die dritte die Intonation. Dann wird ein Rhythmus druntergelegt - fertig ist der Pi-Hit ;-)
❱21❱ ➜ youtube-com-watch?v=Vv3Rve3yXBY
youtube: Herleitung von Pi durch Zahlentheorie, Gauß'sche Zahlen und Zählen von Punkten im Koordinatensystem
❱21❱ ➜ youtube-com-watch?v=Vv3Rve3yXBY
anschauen sollte man sich zur Vorbereitung dazu "Was sind Gauß'sche Zahlen"
❱21❱ ➜ youtube-v=Vv3Rve3yXBY
Was hat Pi mit den Primzahlen zu tun? - eine "fast-Weihnachtsvorlesung" von Prof.Dr.Weitz
❱21❱ ➜ youtube-v=L6APV5Zgc-w
Eine kurze Geschichte der Kreiszahl Pi - Vorlesung von Prof.Dr.Weitz
Pitzig
- An Opinion without 3.14 is an onion
- Why is that ship named 3.14? Because its full of Pi-rates
- My Doctor asked me to rate my pain on a scale of 10 so I told him pi. Pretty low level but never ending
- Love is π : Irrational and never ending
- Was steht auf dem Grabstein eines Mathematikers? - Rest in Pi
- Warum können Seeräuber keine Kreise berechnen? - Weil sie Pi raten.
Kreisumfang + Herleitungen von Pi
➜ Abschnitt ansehen / wegblenden
π beschreibt das Verhältnis vom Umfang eines Kreises zu seinem Durchmesser und stellt eine Proportionalitätskonstante dar. Der
Weltrekord in der Berechnung der Nachkommastellen lag 2016 bei knapp 22 Billionen Stellen - das sind 22 Millionen Millionen Stellen. Wenn man bedenkt, dass die Staatsverschuldung der USA derzeit 19 Billionen US-Dollar beträgt, ist das fast keine gigantische Zahl mehr - oder doch?
- Einfache, experimentelle Berechnung der Kreiszahl π:
1.) Man nehme eine CD / DVD und einen Folienstift.
2.) Man zeichne möglichst genau einen Durchmesser ein. Der Ort für den Mittelpunkt der DVD muss dabei geschätzt werden.
3.) Man zeichne an eine Seite des Durchmessers eine Pfeilspitze.
4.) Der Durchmesser beträgt 12 cm.
5.) Man klebe 2 karierte Blätter zusammen und rolle darauf die CD/DVD ab, um den Umfang zu ermitteln. Es sind ca. 37,7 cm.
6.) Man teile 37,7 durch 12 und erhält 3,1416666
Man wiederhole das Verfahren mit verschiedenen runden Gegenständen
Bei einem Durchmesser mit d = 1 ergibt sich durch U = π * d → U = π = 3,1415926535897
John Reid, CC BY-SA 3.0, http://creativecommons.org/licenses/by-sa/3.0/, via Wikimedia Commons - Pi und die Länge von Flüssen
Der afrikanische Fluss Nil hat mitsamt allen Windungen eine Länge von ca. 6670 Kilometern. Misst man die Luftlinie von der Quelle bis zur Mündung, ergibt das eine Strecke von 2120 Kilometern. Teilt man 6670 durch 2120 ist das Ergebnis 3,14, also "Pi". Das ist so bei allen langen Flüssen auf der Welt. Tatsächliche Länge geteilt durch die Luftlinie ergibt immer mehr oder weniger "Pi".
(Quelle: Wissen macht ah! - ➜ kinder-wdr-de-tv-wissen-macht-ah-bibliothek-zahl-pi-100
Begründung: Im statistischen Mittel ➜ mäandert der Fluss in Halbkreisen bzw. einer Sinuskurve - Pi und die Länge von Seilen
Das "Fluss-Theorem" kann auch im Klassenzimmer mit einem Seil demonstriert werden. Man nimmt ein langes Seil, legt es in Kurven auf den Boden, teilt Distanz durch die Länge des Seiles und welcher Wert ergibt sich näherungsweise? Genau. Dabei müssenn die "Schleifen" jedoch annähernd Halbkreisen oder Sinuskurven ähneln - Pi kann Differentiale zerstören!
Manchmal sind Gespräche beim Reifenwechsel auch für Mathematiker interessant.
"Weshalb müssen bei Fahrzeugen mit Allradantrieb immer alle vier Räder gewechselt werden?"
Begründung:
Falls nicht alle vier Reifen gewechselt werden, haben - durch den Abrieb - zwei Reifen einen anderen Durchmesser. Das sind zwar vielleicht nur 0,5 cm Unterschied (=2,5mm Abrieb) im Durchmesser.
Aber:
Bei einem Reifendurchmesser von 60 cm beträgt der Reifenumfang (die Abroll-Länge) U=π x 60 = 188,5 cm.
Bei einem Reifendurchmesser von 59,5 cm beträgt der Reifenumfang (die Abroll-Länge) U=π x 59,5 = 186,9 cm.
Der Unterschied beträgt im Umfang somit 1,6 cm.
Auf 100 Meter Fahrstrecke beträgt der Abroll-Unterschied der Reifen somit 160 cm. Das Differential gibt beim Allrad auf alle vier Reifen jedoch immer dieselbe Antriebskraft - die Drehzahl der Reifen ist also jeweils gleich groß.
Im besten Fall werden die Reifen, die nicht unter dem Motor liegen (also einem geringeren Anpressdruck und somit einer geringeren Haftung unterliegen) stärker abgenutzt, im (wahrscheinlicheren) Fall wird das Differentialgetriebe durch die ungleichmäßige Belastung zerstört und die eingesparten Kosten für die Reifen werden durch einen Schaden in Höhe von ca. 2000 € für das zerstörte Differentialgetriebe mehr als ausgeglichen. Man sieht: Wissen um π spart Geld und Nerven! - Pi und die Holzstäbchen
❱21❱ ➜ de.wikipedia-org-wiki-Buffonsches_Nadelproblem
Im Buffonschen Nadelexperiment werden Stöckchen (oder Streichhölzer) auf ein Linienraster geworfen. Falls der Abstand d der Linien gleich der Länge l der Stäbchen ist, so erhält man eine Näherung für π , indem man die Anzahl aller genutzten Stäbchen mit 2 multipliziert und durch die Anzahl der Stäbchen, welche eine Linie kreuzen, teilt - Pi und die Ägypter
Die doppelte Basisbreite der Pyramide von Gizeh verhält sich zur Höhe der Pyramide wie π:1. Basisbreite 230,36 Meter, Höhe 146,59 Meter ergibt 460,72/146,59=3,142915615
Die Pyramiden von Gizeh entstanden etwa von 2620 bis 2500 v. Chr. in der 4. Dynastie - Wie die Ägypter π berechnet hatten? Sie legten Pi als 256/81=3,160493827 fest. Nebenbei: Das ist 223/322. Errechnet vor mehr als 3500 Jahren, dargestellt im sogenannten Rhind Papyrus (1650 vor Chr.)
❱21❱ ➜ numberwarrior.wordpress-com-on-the-egyptian-value-for-pi - Pi mit Murmeln
❱21❱ ➜ oxfordconnect-conted-ox-ac-uk-events-2013-pi-day-live-marcus-du-sautoy-find-pi.html#marbles
Das Murmel-Experiment:
Nehmen Sie eine größere Zahl von Murmeln und legen diese auf einer ebenen Fläche zu einem Kreis. Zählen Sie die Zahl der Murmeln am Durchmesser (=D). Zählen Sie die Gesamtzahl der Murmeln des Kreises (=V). Wenn Sie die Gesamtzahl der Murmeln (V) durch die Hälfte der Durchmesser-Murmeln im Quadrat) (D/2)2 teilen, erhalten Sie einen Näherungswert für π
v\(D/2)^2 = л - Im Alten Testament wird π im Zusammenhang mit dem Umfang eines runden Wasserreservoirs als das Dreifache des Durchmessers angegeben.
1.Könige 7, 23 (Elberfelder, 1923) - Pi mit Brüchen
Der Mathematiker Leibnitz leitete Pi wie folgt her: π/4 = 1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + 1/13 - 1/15 .. - Wie weit ist der Nachbarort eigentlich entfernt?
Das kommt auf die Blickrichtung an.
Man stellt zwei Wegweiser zum Nachbarort auf: nach links: "Unterdigisheim 4 km" -- nach rechts: "Unterdigisheim 22.459 km"
Es kommt sicher der Einwand, dass der Erdumfang doch 40.000 km beträgt. Was jedoch nur begrenzt stimmt. Wir nehmen nämlich nicht den längsten Weg, sondern bleiben auf dem Breitengrad. So landet man schließlich bei der Berechnung der Länge des Erdumfangs am Breitengrad mit Pi und den Winkelfunktionen ;-)
Wer den Erdumfang abhängig vom Breitengrad berechnen will, benötigt den Cosinus:
U= 2*Pi*[cos(Breitengrad) * (Radius am Äquator)]
Weshalb das so ist und sich der neue Radius am Kreissegment über die Wechselwinkel ergibt, kann man zusätzlich erklären.
Unterdigisheim liegt laut Wikipedia auf den Koordinaten: 48° 9′ 55″ N, 8° 54′ 37″ O
Benötigt wird hier nur die Breitenkoordinate, also 48° 9′ 55″. Das muss nun in eine Dezimalzahl umgewandelt werden.
Hier hilft siehe auch ➜ Rechneronline und gibt als Ergebnis die Zahl 48,16528 aus.
Das werfen wir in die Formel, gemeinsam mit dem mittleren Erdradius (wer mag darf den gerne für Unterdigisheim noch genau bestimmen), zu dem wir die Höhenmeter addieren.
Gehen wir mal davon aus, dass wir über dem Ural und anderen Mittelgebirgen etwas höher fliegen, dafür auf Meereshöhe uns knapp über der Gischt bewegen, dann sollte das im Mittel passen.
Demnach gilt: r=6.371,000 km + 751 m = 6371,751 km
cos(48,16528) = 0,66698409
U=2*Pi*0,66698409*63710,751=26.702,636 km
Somit sind es von Unterdigisheim nach Unterdigisheim exakt 26.702,636 km
Ätsch. Reingelegt. Stimmt nicht.
Die 200 Meter, die der Wegweiser vom Rathaus entfernt steht, müssen wir nämlich noch abziehen ;-) Soviel sind wir nämlich "andersrum" schon vorbeigelaufen. ;-)
Ätsch. Nochmal reingelegt. Das ist nämlich eine Fermi-Aufgabe. Weil die Erde keine Kugel ist, Hügel und Berge hat, lässt sich das Ganze nur näherungsweise ausrechnen. Die 200 Meter sind also geschenkt.
Und die ,636 auch. 26.700 km passt schon - Man stelle sich vor:
Um die Erde (für dieses Modell als Kugel ohne Berge und Täler), sei um den Äquator ein Seil gespannt.
Was geschieht, wenn man das Seil um einen Meter verlängert - und durch die Verlängerung der Abstand zur Erde ringsherum gleichmäßig verteilt wäre.
Wie groß wäre der Abstand des Seils zur Oberflache dieser Riesenkugel?
Intuitiv denkt man, dass dieser Abstand minimal sein musste. In Wahrheit spielt jedoch der Radius der Kugel überhaupt keine Rolle und der Abstand beträgt 1/(2π)≈0,1592 Meter - bei jeder beliebig großen Kugel. Egal, ob es sich um ein Kügelchen aus dem Kugellager des Fahrrades oder um Jupiter oder die Sonne handelt.
Beweis: Der Kreisumfang betragt U=2*π*r1 (1). Durch die Verlängerung des Seiles wird der Umfang um 1 Meter länger, daher: U+1 = 2*π*r2
Diese Gleichung wird nach U aufgelöst, dadurch ergibt sich U = 2*π*r2 - 1 (2)
U=U, also können Gleichung (1) und Gleichung (2) gleichgesetzt werden, es ergibt sich 2*π*r1 = 2*π*r2 - 1
Wir lösen das System nach r2 auf - denn es soll ja ermittelt werden, um welchen Wert sich r2 verändert.
daher 2*π*r1 + 1 = 2*π*r2
Teilt man beide Seiten durch 2*π ergibt sich r2= r1 + 1/(2*π)
Durch die Umfangsverlängerung um 1 Meter ergibt sich eine Radiusvergrößerung von 1/6,28 m also ≈0,1592 m
Kreisfläche - Eine geometrische Herleitung von Pi
➜ Abschnitt ansehen / wegblenden
Kinder malen mit Zirkeln gerne "Blumen". Eine einfache "Blume" hilft, in den Kreis ein eingeschriebenes Quadrat mit der Seitenlänge r zu zeichnen.
Färbt man die restlichen Flächen entsprechend, können die Schüler leicht erkennen, dass die Kreisfläche etwa drei Mal so groß wie das Radiusquadrat sein muss - man könnte die außen liegenden Flächen ja nach innen auf das grüne Quadrat klappen.
Man sieht auch, dass die Kreisfläche leicht größer als die drei Quadrate sein muss. Eine Zahl, die etwas größer als 3 ist, haben wir bereits kennen gelernt; die Kreiszahl π.
BTW: Wer mag, kann an diesem Beispiel gleichzeitig die Konstruktion des rechten Winkels mit Hilfe des Zirkels thematisieren ;-)

BTW: Damit habe ich übrigens die "Quadratur des Kreises" geschafft, indem ich den Kreis in 3 Quadrate zerlegt habe! Ein lang ungelöstes Problem ist somit gelöst!
BTW: Wer mag, kann an diesem Beispiel gleichzeitig die Konstruktion des rechten Winkels mit Hilfe des Zirkels thematisieren ;-)

BTW: Damit habe ich übrigens die "Quadratur des Kreises" geschafft, indem ich den Kreis in 3 Quadrate zerlegt habe! Ein lang ungelöstes Problem ist somit gelöst!
Kugeloberfläche - experimentelle Herleitung
➜ Abschnitt ansehen / wegblenden
Mit einer Mandarine oder Orange kann die Kugeloberfläche hergeleitet werden:
- - Durchmesser der Mandarine messen und Radius bestimmen - z.B. d=6cm, ergibt r=3cm
- - Auf ein Blatt Papier mehrere Kreise mit dem ermittelten Radius zeichnen (mindestens 4 Kreise)
- - Mandarine schälen, Schale in kleinere Stücke zerteilen, Mandarine essen.
- - Die Schalenstücke möglichst passend in die Kreise legen
- - Ergebnis: Man kann 4 Kreise mit der Schale bedecken.
- - Fläche eines Kreises ist A=πr², die Oberfläche der Kugel somit O=4 πr².
Zylindervolumen + Pizza-Theorem
➜ Abschnitt ansehen / wegblenden
Das "Pizza-Theorem"
Die Formel zur Volumenberechnung eines Zylinders führt zum sogenannten "Pizza-Theorem":Wie groß ist das Volumen einer Pizza mit der Höhe a und dem Radius z?
Antwort: V=Pi*z*z*a
Welches Gewicht trage ich auf meinem Kopf?
Eine Aufgabe, die nur einem Physiker / Mathematiker einfallen kann:Wie schwer ist eigentlich die Luft, die auf meinem Kopf liegt?
So. Da stellen wir uns mal ganz dumm und sagen: Unser Kopf ist kreisrund (oder ein Quadratschädel, wer's noch spezieller will, kann auch von einer Ellipse oder einem Ei ausgehen. Egal. Das hat auf die eigentliche Aufgabe nur geringe Auswirkungen.)
Auf unserem Kopf balancieren wir eine Luftsäule, die bis zur Stratosphäre reicht. Das sind so etwa 100 Kilometer. Der Luftdruck nimmt bis eine eine Höhe von 100 km nur moderat ab. Siehe Grafik.
Wie schwer ist eigentlich Luft? Dazu benötigen wir das spezifische Gewicht. Nehmen wir den Mittelwert von 1,2 kg/m³.
Nun zur Volumenberechnung. Das Volumen einer Säule ist immer Grundfläche mal Höhe. Nehmen wir einen mittleren Durchmesser von 16 cm. Macht 8 cm Radius. Grundfläche somit AG=π * r² = π*8*8 = 200 cm² = 0,02 m².
100 km sind 100.000 m
Die Säule über uns hat demnach ein Volumen V = 0,02 m² * 100.000 m = 2000 m³
Bei einem Gewicht von 1,2 kg / m³ entspricht dies einem Gewicht von 2400 kg oder 2,4 Tonnen.
Man kann das auch einfacher und genauer berechnen. Dazu nehmen wir einfach den Luftdruck.
Der mittlere Luftdruck der Atmosphäre nimmt mit steigender Höhe ab, siehe Grafik.
Da wir uns im Mittel auf vielleicht 500 Höhenmetern bewegen, gehen wir für diese Rechnung jedoch von ca. 950 HektoPascal (hPa) Luftdruck aus, das sind 95000 N/m².
Bei einer Schädeldeckfläche von 0,02 m² drückt somit eine Kraft von 95000*0,02 kg, also 1900 kg Luftsäule=1,9 Tonnen.
Damit sind wir bei beiden Rechenwegen gar nicht so weit auseinander.
Münzvolumen / Silvesterballerei
Welche Länge, Gewicht und Volumen hätte ein Rohr aus den 1€-Stücken, die für das Silvesterfeuerwerk 2019 ausgegeben wurden?Die Bundesbürger haben am Jahreswechsel 2019/2020 für das Silvesterfeuerwerk 137 Millionen Euro verbrannt.
Eine 1-€-Münze hat einen Durchmesser von 23,25 mm, eine Dicke von 2,33 mm und ein Gewicht von 7,50 g. siehe ➜ Wikipedia: Euromünzen
Dies entspricht dem Gewicht von 503 Porsche Cayenne ™ siehe ➜ Daten zum Porsche Cayenne
Das Rohr hätte eine Länge von 137.000.000 x 2,33 mm = 319.210.000 mm = 319.000 m = 319 km. Das ist etwas mehr als die Luftlinie von Frankfurt nach München.
Das Rohr hätte ein Volumen von 319.210.000 mm * 11,625 mm * 11,625 mm * π = 135522774436,677 mm3 = 135522,8 dm3 = 135522,8 Liter = 135 m3
Stapelt man die Euros säuberlich nebeneinander, benötigt jede Münze eine Fläche von 23,25*23,25 mm2=540,5625 mm2 (ohne Verschiebung in die Rundung, sondern als Quadratfläche gerechnet).
Das Volumen wäre dann 540,5625 mm2 * 2,33 mm * 137.000.000 = 172.552.955.625 mm3 = 172.552.956 cm3 = 172.553 dm3 = 173 m3.
Durch die Kubikwurzel ergibt sich eine Kantenlänge von ca. 5,50 m, wenn man die Euros als Würfel stapelt.
Die Summe der Euros hätten ein Gewicht von 137.000.000 * 7,5 g = 1027500000 g = 1027500 kg = 1027,5 Tonnen.
Ein Porsche Cayenne kostet derzeit neu zwischen 75.000 Euro und 135.000 Euro - im Mittel also 100.000 €.
In der Sylvesternacht haben die Bundesbürger den Gegenwert von 137.000.000 / 100.000 = 1.370 Porsche Cayenne verbrannt. Ein Fiat Panda ist für ein Zehntel zu haben. Damit wären es 13.700 Fahrzeuge.
Ernsthafter und betrüblicher:
Weltweit sind 2013 nach Berechnungen der FAO 842 Millionen Menschen, das sind 12 Prozent der Menschheit oder etwa jeder achte Mensch, von Hunger betroffen: Das sind mehr Menschen als sämtliche Einwohner der EU, USA und Kanada zusammengenommen.
Mit 1 € pro Tag kann ein Mensch ernährt werden.
Mit 137 Millionen Euro könnten demnach 137.000.000 / 365 = ca, 375.000 Menschen ein Jahr ernährt werden.
Bierkonsum
Im Jahr 2018 wurden weltweit ca. 1,429 Milliarden Hektoliter Bier gebraut. (Quelle: http://www.bierspot.de/brauereien/die_groessten_brauereien.html) Das sind knapp 143 Milliarden Liter oder 286 Milliarden "Halbe".a) Wie groß wäre eine Bierdose mit dem Standard-Seitenverhältnis (Durchmesser-Höhe), in die die gesamte Weltproduktion passen würde? Eine 1-Liter-Bierdose (1000 cm³) hat eine Höhe von 18 cm und einen Durchmesser von 8,5 cm.
b) Wie viele m² Alublech würden benötigt, wenn die gesamte Weltproduktion nur noch in Dosen ausgeliefert würde?
c) Wie schwer wäre dieses Aluminiumblech?
Bierkonsum 2
Die Weltproduktion an Bier betrug im Jahr 2018 etwa 1,429 Milliarden Hektoliter Bier, das sind 0,286 x 10¹² Halbe - bzw. 0,143 x 10¹² Literdosen.Wie lange müsste man die Weltproduktion für einen "Schlaraffenland-Bodensee" für Männer füllen, bis er mit Bier gefüllt wäre und jeder, der an die Bodenseewasserversorgung angeschlossen ist, sein eigenes Bier zapfen könnte?
Seevolumen: 48 km³ = 48×10¹² Liter
Weltjahresbierproduktion: 0,143 x 10¹² Liter
48×10¹² geteilt durch 0,143 x 10¹² ~ 335,7 Jahre.
Besondere Zahlen: Zahlenfolgen
Erhabene, vollkommene, glückliche, narzisstische, fröhliche und traurige Zahlen➜ Abschnitt ansehen / wegblenden
Besondere Zahlen(reihen)
Die Online-Enzyklopädie der "besonderen Zahlen(reihen) findet sich hier:➜ oeis.org/
Auf dieser Seite sind ALLE Zahlen mit ihren bislang entdeckten Eigenschaften verzeichnet.
Primzahlen
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431,433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557,563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661,673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809,811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937,941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019,1021, 1031, 1033, 1039, 1049,1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153,1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277,1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381,1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487,1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597,1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699,1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823,1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949,1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027➜ archive-org-mathe.tu-freiberg-hebisch-skripte-zahlenth-zahlenth.pdf (längere Ladezeit, da aus archive-org eingebunden)
Beschrieben werden darin die Germain-Primzahlen, Primzahlzwillinge, Primfaktoren der ersten 60 Fibonacci-Zahlen, bekannte Mersennesche Primzahlen, Große Prothsche Primzahlen, Pseudoprimzahlen, Carmichael-Zahlen, Primitivwurzeln modulo p bis 1200...
Primzahlen
- Die erste Primzahl ist die 2 (die 1 ist per Festlegung keine Primzahl!).
Es gibt nur 2 "Sorten" Primzahlen.
Die einen können gebildet werden als (4 * n) + 1, die anderen als (4 * n) - 1
n ist dabei eine ganze Zahl, die aber nicht 'prim' sein muss - Leonhard Euler (Schweizer Mathematiker *1707 †1783) bewies, dass die Primzahlen, die mit (4 * n) + 1 gebildet werden können, immer auch die Summe zweier Quadrate sind.
Beispiel 13 = 2² + 3² - n2+n+41 ergibt stets eine Primzahl, solange n kleiner als 40 ist
- Die folgenden Zahlen sind prim:
31; 331; 3.331; 33.331; 333.331; 3.333.331; 33.333.331; 333.333.331;
Danach bricht diese Reihe jedoch ab. 3.333.333.331 = 673 x 4.952.947 - Primzahlzwillinge werden solche Primzahlen genannt, die eine Differenz von 2 aufweisen - mit Ausnahme von 3 .. 5. so z.B. 5 .. 7 oder 11 .. 13 oder 17 .. 19 oder 29 .. 31 usw.
Aus welchem Grund die dazwischen liegende Zahl immer ein Vielfaches von 6 ist - und ob das eine allgemeingültige Regel darstellt, ist noch nicht geklärt. Die Primzahlzwillings-Vermutung besagt, dass es unendlich viele Primzahlzwillinge gibt. Sie ist eine der großen offenen Fragen der Zahlentheorie.
Primzahlzwillinge haben immer den Wert ( 6 n − 1 , 6 n + 1 ) - In diesem Zusammenhang steht auch " ➜ Belphegor's Primzahl"
1000000000000066600000000000001
Auf die 1 folgen 13 Nullen, darauf die 'Zahl des Tieres' 666, danach wieder 13 Nullen und die 1
Belphegors Primzahl ist das dreizehnte Element der Zahlenfolge der Belphegor-Zahlen - Primzahltupel werden solche Primzahlen genannt, die eine konstante Differenz aufweisen. Beträgt die Differenz 6, handelt es sich um "sexy Primzahlen" ;-)
- Primzahlen ergeben in einer grafischen Darstellung die - nach dem Entdecker - benannte ➜ Ulam-Spirale
Dreieckszahlen
Ein schönes (und einleuchtendes) Beispiel für die Herleitung von Formeln für Zahlenreihen sind die Dreieckszahlen. Die Erläuterung dazu findet sich hier: mathsisfun-com-algebra-triangular-numbers
- Zahlentheoretiker beschäftigen sich seit Jahren mit einer besonderen Zahlengruppe - die Lösungen für sogenannte diophantanischen Gleichungen sind.
Dabei geht es um Polynomfunktionen mit ganzzahligen Koeffizienten und ganzzahligen Lösungen.
Beispiel
Gesucht werden ganzzahlige Lösungen für die Gleichung
k = x³ + y³ + z³
Für Zahlen k, die geteilt durch 9 den Rest 4 oder 5 ergeben wurde gezeigt, dass es keine Lösung geben kann. Das sind zum Beispiel 13, 14 und 22.
1 ist etwa die Summe aus 03 + 03 + 13;
2 kann man als 03 + 13 + 13 darstellen.
Man darf dafür auch negative Zahlen wie -1, -2, -3 verwenden. 6 etwa ist die Summe aus
23 + (-1)3 + (-1)3
Für viele Zahlen gibt es mehrere Lösungen, für bestimmte Zahlen allerdings auch gar keine, was die Zahlentheoretiker ebenfalls interessiert.
Ist die Sache bei 29 noch ganz einfach (33 + 13 + 13), wird es bei 30 überraschend kompliziert: Die Ausgangszahlen vor dem "hoch 3" liegen im Milliardenbereich, wie man erst 1999 entdeckte.
33 = 8.866.128.975.287.5283 + (-8.778.405.442.862.239)3 + (-2.736.111.468.807.040)3
Andrew Booker von der Uni im britischen Bristol löste erst im Frühjahr 2019 die Gleichung für die Summe 33. Das wurde schon gefeiert.
Unter den Zahlen bis 100, die bei Division mit 9 nicht den Rest 4 oder 5 ergeben, war danach nur noch eine Lösung für die 42 offen.
Mitte 2019 konnte nun ebenfalls die Lösung gefunden. 65 Jahre nach dem Stellen des ursprünglichen Problems löste Booker dies nun mithilfe von Andrew Sutherland vom Massachusetts Institute of Technology (MIT) und einer Rechnerkapazität über ein Netzwerk, das ungenutzte Leistung von mehr als einer halben Million Heim-PCs nutzt, wie es in einer Mitteilung heißt.
Die Lösung lautet: 42 = (-80538738812075974)3 + 804357581458175153 + 126021232973356313 - 42stes Gedankenexperiment zur Zweierpotenz
Nimmt man ein normales DIN-A-4-Blatt und faltet es, wird es doppelt so dick. Logisch. Faltet man es nochmal, ist es vier Mal so dick wie das Ursprungspapier. Wie oft müsste man das (Standard-)Schreibmaschinenpapier falten, damit es so dick wäre, damit es die Distanz zum Mond überbrücken würde? Die Antwort lautet - und man verneige sich vor Douglas Adams - 42. 0,1 mm x 2⁴² ergibt etwa 300.000 km - nach 42maligem Falten (was technisch nur im Gedankenexperiment möglich ist), hätte man die Entfernung zum Mond erreicht
Eigenartige Zahlen
- 111.111.111 x 111.111.111 = 12.345.678.987.654.321
- Eine Liste besonderer Zahlen wird in der Wikipedia geführt:
siehe auch ➜ Wikipedia: Liste_besonderer_Zahlen
Erhabene Zahlen
Es sind bislang lediglich zwei erhabene Zahlen bekannt. Die Zahl 12 ist die einzige unter einer Billion.siehe auch ➜ Wikipedia: Erhabene_Zahl
Unter einer erhabenen Zahl oder sublimen Zahl versteht man eine natürliche Zahl, bei der die Anzahl und die Summe ihrer Teiler vollkommene Zahlen sind.
IRI-Zahlen
Bei IRI-Zahlen sind jeweils die Hunderter- und die Einerziffer identisch. Jede IRI-Zahl hat eine "komplementäre" Iri-Zahl (Beispiele: 727-272, 131-313, 919-191 ...). Subtrahiert man jeweils die kleinere von der größeren IRI-Zahl, entstehen 45 IRI-Aufgaben, deren Ergebnis immer ein Vielfaches von 91 ist: 91, 182, 273, 364, 455, 546, 637, 728 und 819. Das Ergebnis ist jeweils die Differenz der Ziffern mal 91. Beträgt die Zifferndifferenz 3, so ist das Ergebnis der Subtraktionsaufgabe 3*91.Beispiel: 727-272 = 5*91 = 455
Spiegelzahlen
Eine Spiegelzahl (Invertzahl, Umkehrzahl oder Kehrzahl) zu einer mehrstelligen natürlichen Zahl erhält man, indem man die Ziffern in umgekehrter Reihenfolge aufschreibt, z. B. ist 4321 Spiegelzahl zu 1234❱21❱ ➜ Wikipedia: Spiegelzahl
12² = 144 | 441 = 21²
112² = 12544 | 44521 = 211²
1112² = 1236544 | 4456321 = 2111²
11112² = 123476544 | 445674321 = 21111²
111112² = 12345876544 | 44567854321 = 211111²
1111112²= 1234569876544|4456789654321 = 2111111²
13² = 169 | 961 = 31²
113² = 12769 | 96721 = 311²
1113² = 1238769 | 9678321 = 3111²
11113² = 123498769 | 967894321 = 31111²
111113² = 12346098769 | 96790054321 = 311111²
1111113²= 123457209969 | 967901165421 = 3111111²
Vollkommene Zahlen
siehe auch ➜ Wikipedia: Vollkommene_Zahl Eine natürliche Zahl n wird vollkommene Zahl (auch perfekte Zahl) genannt, wenn sie gleich der Summe aller ihrer (positiven) Teiler außer sich selbst ist.Die ersten 6 vollkommenen Zahlen sind
6=1+2+3
28=1+2+4+7+14
496=1+2+4+8+16+31+62+124+248
8.128=1+2+4+8+16+32+64+127+254+508+1016+2032+4064
33.550.336=...
8.589.869.056=...
2n-1 × (2n - 1) immer dann eine vollkommene Zahl, wenn 2n - 1 eine Primzahl ist (wie bereits von Euklid bewiesen)
Fröhliche und traurige Zahlen
Zu traurigen, fröhlichen und narzisstischen Zahlen siehe auch den Artikel in: ➜ Spektrum der WissenschaftIn der Zahlentheorie ist im Dezimalsystem eine fröhliche Zahl (vom englischen happy number) eine natürliche Zahl n ∈ N, die als Ausgangswert für eine bestimmte Iterationsvorschrift nach endlich vielen Iterationsschritten zum Zahlenwert 1 führt. ( ➜ https://de.wikipedia.org/wiki/Fröhliche_Zahl)
Beispiel:
n=19 ist eine fröhliche Zahl:
19 ⟶ 12 + 9 2 = 82 ⟶ 8 2 + 2 2 = 68 ⟶ 6 2 + 8 2 = 100 ⟶ 1 2 + 0 2 + 0 2 = 1
Es gibt 143 fröhliche Zahlen, die kleiner oder gleich 1000 sind:
1, 7, 10, 13, 19, 23, 28, 31, 32, 44, 49, 68, 70, 79, 82, 86, 91, 94, 97, 100, 103, 109, 129, 130, 133, 139, 167, 176, 188, 190, 192, 193, 203, 208, 219, 226, 230, 236, 239, 262, 263, 280, 291, 293, 301, 302, 310, 313, 319, 320, 326, 329, 331, 338, 356, 362, 365, 367, 368, 376, 379, 383, 386, 391, 392, 397, 404, 409, 440, 446, 464, 469, 478, 487, 490, 496, 536, 556, 563, 565, 566, 608, 617, 622, 623, 632, 635, 637, 638, 644, 649, 653, 655, 656, 665, 671, 673, 680, 683, 694, 700, 709, 716, 736, 739, 748, 761, 763, 784, 790, 793, 802, 806, 818, 820, 833, 836, 847, 860, 863, 874, 881, 888, 899, 901, 904, 907, 910, 912, 913, 921, 923, 931, 932, 937, 940, 946, 964, 970, 973, 989, 998, 1000, …
(Folge A007770 in OEIS)
Beispiele für fröhliche Primzahlen
Die kleinsten fröhlichen Primzahlen, welche kleiner oder gleich 1000 sind, sind:
7, 13, 19, 23, 31, 79, 97, 103, 109, 139, 167, 193, 239, 263, 293, 313, 331, 367, 379, 383, 397, 409, 487, 563, 617, 653, 673, 683, 709, 739, 761, 863, 881, 907, 937, … (Folge A035497 in OEIS).
Die Carmichael-Zahl n = 1729 ist das Produkt der ersten drei fröhlichen Primzahlen.
Zahlen, die nicht fröhlich sind, sind traurig ;-)
➜ Wikipedia: Traurige (nichtfröhliche) Zahlen
Narzisstische Zahlen (Armstrong-Zahlen)
Die narzisstischen Zahlen sind eine Teilmenge natürlicher Zahlen, die durch bestimmte Rechenvorschriften ihrer Ziffern sich selbst erzeugen.siehe auch ➜ Wikipedia: Narzisstische_Zahl
Ein Beispiel für eine solche Zahl mit der Potenz n=5 ist die fünfstellige Zahl 54748
54748 = 55+45+75+45+85 = 3125+1024+16807+1024+32768 = 54748
Es gibt insgesamt nur 89 narzisstische Zahlen: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407, 1634, 8208, 9474, 54748, 92727, 93084, 548834, … und die größte lautet: 115.132.219.018.763.992.565.095.597.973.971.522.401.
Lego-Reihe
Es ergeben sich folgende Möglichkeiten mit 2x4-Legobausteinen gleicher Farbe Türme zu bauen: (n1)=1, (n2)=24, (n3)=1.560, (n4)=119.580, (n5)=10.166.403, (n6)=915.103.765, (n7)=85.747.377.755, (n8)=8.274.075.616.387, (n9)=816.630.819.554.486, (n10)=82.052.796.578.652.749, ....
https://www.jstor.org/stable/10.4169/amer.math.monthly.123.5.415
Nebenbei: Man muss approx. 40.000.000.000 Legosteine stapeln, um die Distanz Erde-Mond zu überbrücken. Mit den bislang produzierten Steinen könnte man 17 derartige Türme bauen.
Wie viele alternative Varianten diese Türme aufweisen könnten, dürft ihr - durch Fortführung der o.a. Zahlenreihe errechnen ;-)
Wikipedia
❱21❱ ➜ Wikipedia: Zahlensymbolik und Zahlenmystik❱21❱ ➜ Wikipedia: Liste besonderer Zahlen
Youtube
❱21❱ ➜ Zahlenmystik - Teslas Zahlen 3-6-und 9 und QuersummenmystikZahlenmystik, Zahlensymbolik
"Besondere Zahlen":1 - 2 - 3 - 4 - 5 - 6 - 7 - 13 - 18 - 23 - 28 - 36 - 37 - 40 - 42 - 73 - 88 - 187 - 666 und mehr
➜ Abschnitt ansehen / wegblenden
"Ich wenigstens kenne keine vollbefriedigende Erklärung dafür, warum jede ungerade Zahl (von 3 ab), mit sich selbst multipliziert, stets ein Vielfaches von 8 mit 1 als Rest ergibt.", meinte
Erich Bischoff, ein Erforscher der Kabbalah, 1920
❱21❱ ➜ anthrowiki-Numerologie
Die Anthroposophen befassen sich intensiv mit Zahlenmystik - hier findet sich eine Zusammenstellung
❱21❱ ➜ heiligenlexikon-de-Glossar-Zahlenmystik
Im "Heiligenlexikon findet sich ein Kapitel zur Zahlenmystik - dort habe einige Informationen für die folgende Liste entdeckt
❱25Q4❱ ➜ de-numberempire-de
Das Zahlenreich - mit 'zahlreichen' Tools - und einer Suchfunktion für Eigenschaften von Zahlen (unten in der Mitte bei "Zahleneigenschaften")
Magisches und mystisches

Offenbarung des Johannes (66.Buch der Bibel), Kapitel 13 (sic!), Vers 18 (=3x6) (sic!!)
➜ de-wikipedia-org-wiki-Sechshundertsechsundsechzig
Wikipedia
Achtung! Manches, was nun folgt, sind nette Zahlenspielereien, manches - besonders die Buchstabenaliterationen - Internet-Geschwurbel. Obwohl... ;-)
❱21❱ ➜ anthrowiki-Numerologie
Die Anthroposophen befassen sich intensiv mit Zahlenmystik - hier findet sich eine Zusammenstellung
❱21❱ ➜ heiligenlexikon-de-Glossar-Zahlenmystik
Im "Heiligenlexikon findet sich ein Kapitel zur Zahlenmystik - dort habe einige Informationen für die folgende Liste entdeckt
❱25Q4❱ ➜ de-numberempire-de
Das Zahlenreich - mit 'zahlreichen' Tools - und einer Suchfunktion für Eigenschaften von Zahlen (unten in der Mitte bei "Zahleneigenschaften")
1
- Zahl des Einen, Unteilbaren
- Symbol der Individualität
- Sinnbild für den aufrecht stehenden Menschen
2
- Zahl der Verdoppelung und des Gleichgewichts
- Ehepaar, "pari", die erste weibliche Zahl
- Zahl der Dualität und der Ambivalenz von gut - böse, Licht - Dunkelheit, männlich - weiblich, Himmel - Erde, Yin - Yang
3
- Zahl der Trinität: Gott-Vater - Sohn - Heiliger Geist (Christentum) // Osiris - Isis - Horus (Ägypt.Mythologie) // Brahma - Vishnu - Shiva (indische Mythologie) // Körper, Seele und Geist
- "Omne trium perfectum": alle Dreiheit ist vollkommen - "Aller guten Dinge sind drei"
- Es gibt 3 Erzengel (Michael, Gabriel und Raphael)
- Heilige 3 Könige: Caspar, Melchior und Balthasar
- 3 Stunden litt Jesus am Kreuz
- 3 göttliche Tugenden: Glaube - Hoffnung - Liebe
- 3 Mal wurde Christus von Petrus verleugnet (Matthäusevangelium 26, 69 - 74)
- Die Zahl 3 ist die erste Mersenne-Primzahl
4
- 4 Himmelsrichtungen
- 4 Jahreszeiten
- 4 Elemente: Feuer - Erde - Wasser - Luft
- 4 Temperamente: Phlegmatiker - Sanguiniker - Choleriker - Melancholiker
- 4 Kardinaltugenden: Klugheit/Weisheit - Gerechtigkeit - Tapferkeit - Mäßigung
- 4 Flüsse im Paradies
- 4 Erzengel: Michael - Gabriel - Raphael - Uriel
- 4 apokalyptische Reiter: Krieg - Gemetzel - Hunger - Tod
- 4 Patriarchalbasiliken in Rom: Petersdom - San Paolo fuori le Mura - San Giovanni in Laterano - Santa Maria Maggiore
5
- Fünf Sinne hat der Mensch: Sehen - Hören - Riechen - Schmecken - Tasten (Wobei der Gleichgewichtssinn hier unterschlagen wird)
- 5 "Säulen des Glaubens" (rituelle Hauptpflichten) gibt es im Islam: Schahada (Bekenntnis des Einen Gottes und seines Propheten) - Salah (das rituelle Gebet) - Zakat (die Abgabe für Bedürftige) - Saum (das Fasten im Ramadan) - Haddsch (die Pilgerfahrt nach Mekka)
- Das Pentagramm gilt auch als magisch-abwehrendes Zeichen gegen das Böse
- In der Antike waren 5 Planeten bekannt
- 5 törichte und 5 kluge Jungfrauen werden zur Hochzeit geladen (Matthäusevangelium 25, 1-13)
- 5 Wundmale wurden Jesus Christus am Kreuz zugefügt
6
- 6 Flächen besitzt der Spielwürfel
- 6 entspricht der Summe seiner Teiler: 1 + 2 + 3 = 6. Sie ist die vierte "perfekte (vollkommene) Zahl"
- Ergebnis der Multiplikation der ersten weiblichen (2) mit der ersten männlichen (3) Zahl
- 6 zeigt sich im Hexagramm und im Davidsstern
- In der Offenbarung des Johannes steht die Zahl 6 als Symbol des Bösen. 666 ist die Zahl des apokalyptischen Tieres (siehe unten)
- In der Bibel wird von 6 Teufelsausbreitungen durch Jesus berichtet
7
- Die "Glückszahl" - In China oder Thailand jedoch eine Unglückszahl
- Ein Siebtel lässt sich über Vielfache von 7 berechnen - dabei wird jeweils die Verdoppelung der zuletzt angehängten Zahl angefügt, dabei von rechts zwei Ziffern verschoben.
Die Summe der Zahlen ergibt den Dezimalbruch von 1/7:
0.14 → 14*2=28
+0.0028 → 28*2=56
+0.000056 → 56*2=112
+0.00000112 → ...
+0.0000000224
+0.000000000448
+0.00000000000896
+0.0000000000001792
+0.000000000000003584
+0.00000000000000007168
+0.0000000000000000014336
+0.000000000000000000028672
+0.00000000000000000000057344
+0.0000000000000000000000114688
+0.000000000000000000000000229376
und so weiter - dann aufaddieren und es ergibt sich
___________________________________________
≈0.142857142857142857142857 - Die gegenüber liegenden Augen eines Spielwürfels ergeben in der Summe immer 7
- Sieben Sinne: Sehen, Hören, Riechen, Schmecken, Tasten, Orientierung und Gleichgewicht
- Der Mensch besitzt 7 Körperöffnungen
- Durch die Addition der ersten sieben Zahlen 1+2+3+4+5+6+7 ergibt sich 28 - die Anzahl der Tage im Mondzyklus / Menstruationszyklus
- In der Offenbarung des Johannes, einem Brief an sieben Gemeinden, in dem die Apokalypse vorhergesagt wird, wird die Sieben 54-mal genannt: Das Buch mit sieben Siegeln, die sieben Posaunen, die jeweils eine weitere Endzeit-Erscheinung einläuten, sieben Schalen, sieben Plagen, ein siebenköpfiges Tier
- Im katholischen Glauben gibt es
sieben Tugenden: Glaube, Hoffnung, Liebe, Klugheit, Gerechtigkeit, Tapferkeit, Mäßigung
sieben Laster (Todsünden): Stolz, Geiz, Wollust, Neid, Völlerei, Zorn, Trägheit,
sieben Sakramente: Taufe, Firmung, Eucharistie, Beichte, Ehe, Priesterweihe, Krankensalbung
sieben Gaben des Heiligen Geistes: Weisheit, Verstand, Rat, Stärke, Wissenschaft, Frömmigkeit, Gottesfurcht
sieben Werke der Barmherzigkeit: Hungrige speisen, Durstige tränken, Fremde beherbergen, Nackte kleiden, Kranke pflegen, Gefangene besuchen, Tote bestatten - 7 Schmerzen hatte Maria zu erdulden und 7 Dämonen hatten Maria Magdalena besessen
- ➜ 7 letzte Worte (Sätze) sprach Jesu am Kreuz (Link zur Wikipedia)
- 7 Tage dauerte nach der Bibel die Schöpfung - daraus ergab sich die Festlegung auf 7 Wochentage
- 7 "fette" und 7 "magere" Jahre prophezeite Josef dem Pharao in Ägypten (1. Mose 41)
- In der griechischen Überlieferung gibt es
sieben freien Künste: Grammatik, Rhetorik, Dialektik, Arithmetik, Geometrie, Musik, Astronomie - Im Islam gibt es
im Gebet 7 Bewegungsarten
die Vorschrift in Mekka die Kaaba 7-mal zu umkreisen - Der Buddhismus kennt 7 Himmel
- Es gab 7 Weltwunder
- 7 Zwerge wohnen im Märchen hinter den 7 Bergen
- Es ist nicht möglich, ein regelmäßiges Siebeneck alleine mithilfe von Zirkel und Lineal zu konstruieren.
- Die Zahl 7 ist die zweite Mersenne-Primzahl
13
- Die Angst vor der Zahl 13 wird wissenschaftlich als "Triskaidekaphobie" bezeichnet.
siehe auch ➜ ewigeweisheit-de-bibliothek-numerologie-zahlenmystik-die-dreizehn-13
Hier verschwurbelt jemand verschiedene Zahlen mit mystischen Begriffen. Weil dabei auch mathematische Zusammenhänge gezeigt werden, lass ich das mal so stehen ;-)
Die Angst vor dem "Unglückstag Freitag, dem 13ten" wird Paraskavedekatriaphobie genannt - über gr. parascevi = Tag vor Samstag (=Freitag), dekatria=13, Phobie=Angst - Die Zahl 13 ist eine MIRP-Zahl (die Spiegelzahl 31 ist ebenfalls prim)
14
Die Zahl 14 steht für die "14 words" (englisch: "We must secure the existence of our people and a future for white children", bedeutet: "Wir müssen die Existenz unseres Volkes und eine Zukunft für weiße Kinder sichern"). Diese Bezeichnung wurde (und wird) von US-amerikanischen Rassisten verwendet.18
In der Neonazi-Szene steht diese Zahlenkombination synonym für "Adolf Hitler" = AH (1. und 8.Buchstabe des Alphabets)23
- Auch um die Zahl 23 ranken sich Verschwörungstheorien und Phantasien. Die Zuschreibung der Zahl 23 ist jedoch noch nicht sehr alt.
siehe auch ➜ die23er-de - Autor William S. Burroughs machte 1967 die Welt in seiner Kurzgeschichte „23 Skidoo“ darauf aufmerksam, dass die 23 das Tor in eine andere Dimension sei und auch von Außerirdischen benutzt werde
- "23 Skidoo" war bereits in den USA der 20er Jahre eine sehr bekannte Redewendung, die soviel bedeutete wie "rasch abhauen"
- Im Roman „Illuminatus“ von Robert Shea und Robert Anton Wilson wurde die Zahl aufgegriffen und seither als "Die geheime Zahl der Illuminaten" bezeichnet. Durch Buch und Film blieb diese Zahl jedoch nicht lange geheim ;-)
- Die Ursache für diese Zahlvorstellung könnte darin liegen, dass die 'Offenbarung des Johannes' über den Untergang der Welt aus 23 Kapiteln besteht.
- Weil bei jedem Fußballspiel zusammen mit dem Schiedsrichter 23 Personen auf dem Platz sind, können nun auch diese als "Erleuchtete" gemeint sein. ;-)
- Die Zahl 23 setzt sich aus den beiden kleinsten Primzahlen 2 und 3 zusammen und ist selbst eine Primzahl
- Die Zahl 23 ist eine "sexy" Primzahl. Die Differenz zu den nächsten Primzahlen 17 und 29 beträgt jeweils 6 und ist somit Teil eines "sexy Primzahldrillings"
- 2:3 ist 0,666 - teuflisch aber auch. Wobei diejenigen, die daher die 23 als teuflische Unglückszahl propagieren, nicht rechnen können ;-)
- Der Mensch besitzt 23 Bandscheiben
- Die Quersumme der Zahl PI (3,14159...) beträgt bis zur 5. Stelle nach dem Komma 3+1+4+1+9+5 = 23
- 23! (23 Fakultät) hat im Ergebnis genau 23 Stellen: 1 * 2 * 3 * ... * 22 * 23 = 25.852.016.738.884.976.640.000
28
Steht für die verbotene Organisation "Blood & Honour" (2. und 8.Buchstabe des Alphabets)31
- Die Zahl 31 ist die dritte Mersenne-Primzahl
- Die Zahl 31 ist eine MIRP-Zahl (die Spiegelzahl 13 ist ebenfalls prim)
36
- 22 x 32 = 36
- Faktoren 1,2,3,4,6,9,12,18,36
- Die Summe der Zahlen von 1-36 ergibt 666 - die "Zahl des Tieres" = "Teufelszahl"
- Darstellung im Dualsystem: 100100
- Die Summe im MagischenQuadrat mit 36 Feldern ergibt ebenfalls 666
- 36*37 = 2*666
- Das Roulette hat 37 Kugeln (beschriftet mit 0 - 36)
- Ein Kleinbildfilm hat 36 Bilder mit je 36 mm Breite und 24 mm Höhe
- (666+666)-(36*36)=36
- 360-(6+6+6)(6+6+6)=36
- Pascalsches Dreieck für Esoteriker
6
6 6
6 12 6
6 18 18 6
6 24 36 24 6 - 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36
- 1 + 3 + 5 + 7 + 9 + 11 = 36
37
- 37 ist eine Primzahl. Sie ist auch eine "sexy Prime", weil der Abstand zur nächst niederen und höheren Primzahl jeweils 6 beträgt (31, 37, 43)
- Die Zahl 37 ist eine MIRP-Zahl (die Spiegelzahl 73 ist ebenfalls prim)
- Die Differenz der "Spiegelzahlen" 73 und 37 ergibt 36 (= 6*6)
-
111 / (1+1+1) = 37
222 / (2+2+2) = 37
333 / (3+3+3) = 37
444 / (4+4+4) = 37
555 / (5+5+5) = 37
666 / (6+6+6) = (6*6)+1 = 37
777 / (7+7+7) = 37
888 / (8+8+8) = 37
999 / (9+9+9) = 37 - 37 ist Primfaktor von 111 (=3·37)
- 37 ist Primfaktor von 111111 (= 3·7·11·13·37)
- 37 ist die dritte ➜ Sternzahl, die Zahl von Punkten in einem Hexagramm.
- Das Roulette hat 37 Kugeln (beschriftet mit 0 - 36)
- 36*37 = 2*666 (siehe 666)
40
- Die Fastenzeit wird in der Bibel mit 40 Tagen angegeben - Jesus hatte laut Bibel 40 Tage in der Wüste verbracht. Von Aschermittwoch bis Ostern sind es jedoch 46 Tage - und nicht 40. Weshalb das so ist, habe ich ➜ hier beschrieben. Die Zahl 40 findet sich in der Bibel immer wieder. 40 Tage nach Ostern ist Christi Himmelfahrt, 50 Tage nach Ostern ist Pfingsten, 40 Tage nach Weihnachten ist Lichtmess
- Christentum und Islam sind in ihren Traditionen nicht so weit auseinander, wie manche Leute glauben (machen wollen). Das "Fastenbrechen" am Ende des Ramadan hat sein cristliches Äquivalent im Osterfest, sowie in der Weihnachtsfeier und dem Advent, der noch heute in den orthodoxen Kirchen als Fastenzeit begangen wird - so wie vermutlich auch im Westen bis zum Jahr 1200. Die Philippus-Fastenzeit dauert nebenbei bemerkt - wie in der christlichen Zahlenmystik üblich - 40 Tage. ➜ Wikipedia: Philippus-Fastenzeit
- Die Sintflut dauerte 40 Tage, 40 Jahre wanderten die Jsraeliten durch die Wüste, Moses fastete 40 Tage auf dem Berg Sinai
- Im Islam wird ein Neugeborenes 40 Tage nach seiner Geburt der Familie und den Freunden präsentiert
- 40 Tage, nachdem ein Angehöriger gestorben ist, kommen im Islam Verwandte und Freunde wieder zusammen, um den Toten zu ehren
- 40 Tage lang mussten ab dem 14. Jahrhundert Schiffe vor dem Hafen ankern, damit niemand die Pest einschleppt. Davon leitet sich der Begriff "Quarantäne" ab
42
- Die Erklärung für das Universum und den ganzen Rest
Im Roman "Das Restaurant am Ende der Galaxis" von Douglas Adams taucht ein Computer auf, dem vor Millionen Jahren die Aufgabe gegeben wurde, den Sinn des Lebens zu berechnen. Es zeichnet sich das Ende der Berechnungen ab und als Lösung für den Sinn gibt der Computer die Zahl "42" aus. (siehe auch Sheldon-Zahl)
Seit Erscheinen des Romans ist die "42" daher "Kult".
Adams meinte in einem Interview dazu 1993:
"Die Antwort darauf ist ganz einfach. Es war ein Scherz. Es musste eine Zahl sein, eine gewöhnliche, kleine Zahl, und ich habe diese gewählt. Binäre Darstellungen, Basis 13, tibetische Mönche sind allesamt Unsinn. Ich saß an meinem Schreibtisch, starrte in den Garten und dachte, „42 passt“. Ich habe es getippt. Ende der Geschichte." - Nichtsdestowenigertrotz:
- Im dezimalen ASCII-Code steht die 42 für den Asterisk (*) - sic!
- 42 Kilometer beträgt die Entfernung im Marathon - 42,195 Kilometer - um genau zu sein. Diese "krumme Distanz" wurde 1908 etwas skurril festgelegt.
Bis dahin mussten beim Marathon 25 Meilen (=40,23 km) zurückgelegt werden. Bei den olympischen Spielen in London 1908 wurde der Endpunkt des Laufes direkt vor die königliche Loge von Schloss Windsor gelegt.
Dieser Punkt lag exakt 42,195 Kilometer vom Start entfernt. Aus diesem Grund sollen noch heute angelsächsische Marathonläufer auf dem letzten Kilometer ein "God Save the Queen" ausstoßen. ;-)
Quelle: ➜ Wikipedia: Marathonlauf - Zweite ➜ primär pseudovollkommene Zahl
- Fünfte ➜ Catalan-Zahl. Diese sind extrem selten: Nur 14 davon sind kleiner als eine Milliarde. Leonhard Euler erwähnte erstmals Catalan-Zahlen, als er untersuchte, wie man ein n-seitiges konvexes Vieleck in Dreiecke zerlegen kann
- Kleinstdimensionaler Raum ohne ➜ Wurstkatastrophe. Dabei wird die optimale Anordnung von Kugeln in beliebigen Dimensionen des euklidischen Raums untersucht
- 42 ist eine 'Praktische Zahl', das heißt, jede kleinere Zahl lässt sich als Summe von paarweise verschiedenen echten Teilern schreiben. Die ersten praktischen Zahlen sind 1, 2, 4, 6, 8, 12, 16, 18, 20, 24, 28, 30, 32, 36, 40, 42, 48, 54, 56, 60, 64, 66, 72, …
Beispiele für die Zahl "28" (Quelle: Wikimedia)
Für 42: Teiler sind 1,2,3,6,7,14,21. Die Vorgängerzahl 41 lässt sich schreiben als Summe der Teiler 21+14+6 - Im Binärsystem hat die 42 die prägnante Form 1010102 (= 25 + 23 + 21). Dabei handelt es sich um ein Element der Folge a(n), der Summe ungerader Zweierpotenzen
- 42 ist die Summe der ersten beiden Potenzen von sechs (61 + 62 = 42)
- Im Roman erwähnt Douglas mehrmals, dass 42 die Antwort auf "6x9" sei. Im Zehnersystem macht dies keinen Sinn. Im 13-er System ist 42 jedoch die entsprechende Zahl für die 54 im Zehnersystem, nämlich 4×13 + 2×1 = 54 = 4213
- Ein magischer Würfel der dritten Ordnung hat die magische Zahl 42
- Die Zahl 808080808 besitzt die Quersumme 42
- 42stes Gedankenexperiment zur Zweierpotenz
Nimmt man ein normales DIN-A-4-Blatt und faltet es, wird es doppelt so dick. Logisch. Faltet man es nochmal, ist es vier Mal so dick wie das Ursprungspapier. Wie oft müsste man das (Standard-)Schreibmaschinenpapier falten, damit es so dick wäre, damit es die Distanz zum Mond überbrücken würde? Die Antwort lautet - und man verneige sich vor Douglas Adams - 42. 0,1 mm x 242 ergibt etwa 300.000 km - nach 42maligem Falten (was technisch nur im Gedankenexperiment möglich ist), hätte man die Entfernung zum Mond erreicht - ➜ spektrum--die-geheimnisse-der-zahl-42
Weshalb die 42 bedeutsam ist - Bei folgendem Problem hatten sich die Mathematiker bis 2019 die Zähne ausgebissen:
Kann die 42 auch als Summe dreier ganzzahliger Kubikzahlen geschrieben werden? (n = a3 + b3 + c3)
Weil Kubikzahlen für ein gegebenes n auch negativ ausfallen können, fällt das Problem sehr kompliziert aus. Denn die Zahlenwerte von a, b, c sind dadurch unbegrenzt.
Im September 2019 kam schließlich die Antwort – gerade einmal sechs Monate nach der Lösung für die 33. Es war das Ergebnis einer gewaltigen Berechnung, die Andrew Booker und Andrew Sutherland koordinierten. Die enorme Leistung erbrachten mehrere private Computer, die Teil des Netzwerks »Charity Engine« waren, das die Rechenzeit Universitäten und anderen Projekten zur Verfügung stellt. Nach zusammengerechnet mehr als einer Million Stunden Rechendauer (sic!) fanden sie folgendes Ergebnis:
42 = (– 80.538.738.812.075.974)3 + 80.435.758.145.817.5153 + 12.602.123.297.335.6313
zitiert aus: spektrum--die-geheimnisse-der-zahl-42 - Während des Totengerichts musste ein Verstorbener nach ägyptischem Glauben vor 42 Richtern erklären, dass er in seinem Leben keine von 42 Sünden begangen hatte
- Tibet hatte 42 Könige. Nyatri Tsenpo, regierte als erster um 127 v. Chr. und Langdarma von 836 bis 842 n.Chr. als letzter
- Das erste in Europa gedruckte Buch, die Gutenberg-Bibel, hat 42 Textzeilen pro Spalte. Sie wird auch "zweiundvierzigzeilige Bibel" genannt
- Die buddhistische Göttin Guanyin/Kannon des Mitgefühls besitzt eigentlich 1000 Arme, wird jedoch oft mit 42 Armen dargestellt.
- Bibel: Die Leviten besaßen sechs Zufluchtsstätten, denen noch 42 weitere hinzugefügt wurden (Buch Mose 35.6). Asmaweth hatte 42 Söhne (Buch Esra 2.24)
- In Kapitel 12 von "Alice im Wunderland" nennt der König die älteste, 42. Regel im Ort: "Alle Personen, die mehr als eine Meile hoch sind, haben den Gerichtshof zu verlassen!"
- Funfact: Im Sketch von 'Monty Pythons Flying Circus': "The Light Entertainment War" spielt Douglas Adams in Folge 42 einen Arzt
- Last - but not least: Die Bundesregierung legte 2021 [(2+0)*21] durch einen komplizierten Algorithmus auf Basis der Zahl 42 den Inzidenzwert für die Schließung der Schulen fest: 42 x 4 - (4 + 2 ) / 2 = 165
- Eine alte Version der Verfilmung ist hier zu finden: youtube=RnIMSrWQ8U0
- Sucht man in der Zahl π nach der Antwort auf alle Fragen - der Zahl 42 - ist das unspektakulär. Sie erscheint an Position 92. Die Zahl 42424242 erscheint jedoch an Position 242422, nimmt man die 3 und den Punkt dazu, ist es Position 242424
63
- Die Zahl 63 ist die sechste Mersenne-Zahl
Im Dualsystem besteht sie aus 6 Einsen: 11111112
Sheldon-Primzahl 73
- In der
➜ 73. Folge der Kultserie 'The Big Bang Theory' ) (Staffel 4, Folge 10) erklärt Sheldon, weshalb für ihn 73 die 'beste bekannte Zahl' ist:
Dialog:
"Welches ist die beste Zahl, die bekannt ist? Aber bedenkt: Es gibt nur eine korrekte Antwort. [...]
Die beste ist nämlich die 73. Ihr fragt Euch bestimmt wieso.
Die 73 ist die 21. Primzahl, ihre Spiegelzahl die 37 ist die 12. Primzahl, deren Spiegelzahl 21 ist das Produkt der Multiplikation von - haltet Euch fest - 7 und 3. Na, na, was hab ich gesagt.
Leonard: "Schon klar, die 73 ist der Chuck Norris des Zahlenuniversums."
Sheldon: "Das hätte Chuck Norris wohl gern. Binär ausgedrückt ist die 73 ein Palindrom: 1001001, rückwärts 1001001, also exakt dasselbe. Chuck Norris ergibt rückwärts einfach Sirron Kcuhc."
Dieser Dialog war zunächst nur eine Anspielung auf das Geburtsjahr 1973 von Jim Parsons (Darsteller von Sheldon), es sich um die 73.Folge handelte und Jim Parsons im Produktionsjahr 37 Jahre alt wurde. Die interessante Spiegelzahleigenschaft eignete sich zudem als guter Gag für das Drehbuch der Serienfolge.
Das Zahlenspiel hat zwei Mathematiker zu Forschungen angeregt, ob weitere Zahlen mit derselben Eigenschaft existieren.
"Carl Pomerance vom Dartmouth College und Chris Spicer vom Morningside College (definierten) eine Sheldon-Primzahl y sinngemäß als die n-te Primzahl y, wobei das Produkt der Ziffern von y wieder n ergibt und die Spiegelung der Ziffern von y die m-te Primzahl. Und m soll dann auch noch die Spiegelung von n sein ...
"Erst jetzt konnte er jedoch gemeinsam mit Pomerance zeigen, dass die Sheldon-Bedingungen für Primzahlen größer als 10 hoch 45 nicht erfüllt werden können. Danach konnten die beiden Mathematiker mit allerlei Einschränkungen und Tricks den Zahlenraum bis zu dieser riesigen Zahl per Algorithmus abgrasen, und so beweisen: Die 73 ist die einzige Sheldon-Primzahl, die es gibt."
➜ Quelle: Süddeutsche Zeitung 23.Mai 2019
Der ausführliche Beweis wurde hier veröffentlicht:
➜ math-dartmouth.edu-sheldon02132019 >
- 73 ist die 21. Primzahl, ihre Spiegelzahl die 37 ist die 12. Primzahl, deren Spiegelzahl 21 ist das Produkt der Multiplikation von 7 und 3
- Die Spiegelzahl 37 ist eine " ➜ Einzigartige Primzahl"
- Die 73 ist die sechste 'Mirpzahl'. Eine Mirpzahl ist eine Zahl, die rückwärts gelesen wiederum eine Primzahl ergibt; hier: 37 - ("Mirp" = Palindrom von "Prim").
Bislang sind erst 24 Mirpzahlen, auch 'permutierbare Primzahlen' oder 'absolute Primzahlen' bekannt - Die Quersummen von 73 und 37 sind jeweils 10. Was auch die Quersumme ihres Produkts (2701) ist. Addiert man die erste und letzte Stelle des Produkts zur mittleren Zahl, erhält man 37 respektive 73
- Die Ziffernanzahl und -summe der binären Darstellung von 73 == 1001001 sind 7 und 3
- 73 = 1 + 23(1 + 23) = 1 + 23+ 26
- 73 = 13 + 23 * 32 = 1 + 1 * 2 * 2 * 2 * 3 * 3 = 1 + 3 * 24 = 1 + 2 * 3 * 12 = 1 + 2 * 3 * 4 * 3
- a(n)=x2 + 3*y2
73 = 8*8 + 3*22 - a(n)=x2 + xy + y2
73 = 8*8 + 8*1 + 1*1 - a(n)=x2 + y2
73 = 82 + 32 - 7337≡17 mod 77
- 73 ist als Binärzahl ein Palindrom (eine Spiegelzahl): 1001001, rückwärts ebenso 1001001
Diese Binärzahl enthält 7 Stellen, davon sind 3 Einsen - 73 == 343 ist ein Palindrom, wenn man die ersten beiden Ziffern durch die Summe der Ziffern ersetzt. (7=3+4)
- Die Zahl 21 besitzt die Primfaktoren 7 und 3. Die Zahl 21 ist binär 10101; Die Zahl 7 ist binär 111, 3 ist binär 11 und 73 ist binär 1001001. Alle diese Binärzahlen sind Palindrome
- 37 + 12 = 49 (=72) sowie 73 + 21 = 94 = 47 × 2,
47 + 2 = 49 (=72) - 73 ist die 21.Primzahl
Die Spiegelzahl von 21 ist 12
212=441
122=144
Die Ergebnisse sind wieder Spiegelzahlen: 144 --- 441 - 37!+1 ist eine Primzahl, genauso 73!+1
- 37 ist Primfaktor von 111 (=3·37)
37 ist Primfaktor von 111111 (= 3·7·11·13·37)
73 ist Primfaktor von 11111111 (= 11·73·101·137)
wobei die Primfaktoren jeweils aus den Ziffern 0,1,3,7 bestehen - 73 ist das vorletzte Resultat der größten rechtsstutzbaren Primzahl im Dezimalsystem:
Die größte rechtsstutzbare Primzahl im Dezimalsystem ist 73.939.133
Eine rechtsstutzbaren Primzahl ist eine Zahl, für die gilt, dass bei Wegstreichen der letzten Ziffer wieder eine Primzahl mit genau dieser Eigenschaft entsteht. 7393913, 739391, 73939, 7393, 739, 73 , 7 sind ebenfalls jeweils Primzahlen. - Die 73 ist auch die 18. glückliche Zahl.
Glückliche Zahlen sind 'überlebende Zahlen' im "Streichverfahren"
➜ Wikipedia: Glückliche Zahlen - 73 ist Teil des Primzahlzwillings (71,73)
- 73 ist Teil eines doppelten"Sexy Prime-Paares", Primzahlen sind "sexy, wenn der Abstand zur nächsten Primzahl 6 beträgt:
(67,73), (73,79)
Die Spiegelzahl 37 ist ebenfalls "sexy Prime" (31, 37)
siehe ➜ Sexy Primes - 73 ist Teil des "Sexy Prime-Drillings"
(67,73,79) - 73 ist Teil des "Sexy Prime-Vierlings"
(61,67,73,79) - 73 oktal = 111. Spiegelzahl ebenso 111. Es ist die einzige prime "Repunit" im Oktalsystem
- 73=49hex, 37=25hex, 49 und 25 sind Quadratzahlen (7*7) und (5*5). Die Differenz von 73 und 37 ergibt 36 (=6*6)
- 73 im Morsecode – – · · · · · · – – (ebenfalls ein Palindrom)
Der symmetrische Code wurde in den frühen Jahren der Landtelegrafie zur Übermittlung "Herzlicher Grüße" verwendet und die Zahl 73 daher von Funkamateuren oft ebenfalls ans Ende ihrer Nachrichten gesetzt.
Die 73 ist im Amateurfunkdienst die Abkürzung/Schlussformel für „Viele Grüße“ - 37 und 73 sind die dritte und die vierte
➜ Sternzahl, die Zahl von Punkten in einem Hexagramm.
Die n-te Sternzahl ergibt sich mit der Formel Sn = 6n(n − 1) + 1.
*
* *
* * * * * * *
* * * * * *
* * * * *
* * * * * *
* * * * * * *
* *
*
Die ersten 20 Sternzahlen für Hexagramme sind
1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, 937, 1093, 1261, 1441, 1633, 1837, 2053, 2281,
Die ersten Stern-Primzahlen lauten 13, 37, 73, 181, 337, 433, 541, 661, 937 - Das Doppelte von 37 ist 74 (= 73 + 1), die Folgezahl von 73
- Jede natürliche Zahl kann als Summe von höchstens 73 Potenzen der Ordnung 6 geschrieben werden,
➜ siehe Waringsches Problem
Erstaunlich dabei: g(5)=37, g(6)=73 - 42 hat Konkurrenz bekommen !!!!
Wobei..... 7*3 *2 = 42 --------- 3*7 *2 = 42
Zudem: 7-3 gibt 4 , 3-7 ergibt -4 ... und wieder spiegeln sich 2 Zahlen ;-) - 73 = (1 + 1) * 42 - 11
- Zudem..... 7*3 = 21 --------- 3*7 = 21
21 + 21 = 42 ;-) - ➜ Heise: Zahlen-bitte-Ist-73-die-beste-Zahl
- ➜ spektrum-de-news-sheldon-vermutung-geloest
- ➜ bigbangtheory-fandom-com-de-wiki-73 - Der Dialog
- Zusätzlich dazu, dass die Zahl 21 die Primfaktoren 7 und 3 besitzt, entspricht sie im Dreiersystem (Stellenwertsystem zur Basis 3) der Dezimalzahl 7: 213=710
Magisches und mystisches
- Es dauerte 73 Sekunden, bis das Space Shuttle Challenger OV-099 nach dem Start explodierte
- 73 is the number of rows in the 1,679-bit Arecibo message, sent to space in search for extraterrestrial intelligence
- Nach katholischer Lehre enthält die Bibel 73 Schriften des Alten und des Neuen Testaments
88
- In der Naziszene synonym für "Heil Hitler" = HH (8.Buchstabe des Alphabets)
- Es gibt genau 88 Möglichkeiten, das ➜ Haus vom Nikolaus zu zeichnen.
Hier sind sie im Video dargestellt: youtube-watch?v=YTAAp4Fk4R8. Diue Zeichnung gelingt nur, wenn man von einem der beiden unteren Eckpunkte aus startet.
127
- Die Zahl 127 ist die vierte Mersenne-Primzahl und die siebte Mersenne-Zahl
Im Dualsystem besteht sie aus 7 Einsen: 11111112
137
- Alle hinreichend großen Zahlen sind Summen von höchstens 137 siebten Potenzen
- Die Feinstrukturkonstante α ≈ 1/137 tritt in der Theorie der Atomspektren auf. Das Besondere: α ist dimensionslos, ein reiner Zahlenwert ohne Einheit wie zum Beispiel Zentimeter oder Kilogramm.
Die Zahl ist das Ergebnis einer eigentümlichen Kombination der drei Naturkonstanten e (elektrische Ladung), h (Wirkungsquantum) und c (Lichtgeschwindigkeit).
Sie verknüpft also Quantentheorie (e, h) und Spezielle Relativitätstheorie (c) und ist daher ein zentrales Element der Relativistischen Quantenmechanik.
Quelle: ❱25Q4❱ ➜
https://www.spektrum.de/rezension/137/1117013
Spektrum der Wissenschaft: "Die mystische Zahl", Rezension vom 19.07.2011
187
- Die Zahl 187 ist die Nummer des Paragrafen im kalifornischen Strafgesetzbuch, der Mord behandelt. Der Code „One-Eight-Seven" wird im amerikanischen Polizeifunkverkehr genutzt
- Verschiedene Gangs und Rapper haben das aufgegriffen und benutzen den Code, um klarzustellen, dass sie auch zu einem 1-8-7 bereit wären, also einem Mord
666
Die Teufelszahl = "The number of the Beast"
Offenbarung des Johannes (66.Buch der Bibel), Kapitel 13 (sic!), Vers 18 (=3x6) (sic!!)
➜ de-wikipedia-org-wiki-Sechshundertsechsundsechzig
Wikipedia
Achtung! Manches, was nun folgt, sind nette Zahlenspielereien, manches - besonders die Buchstabenaliterationen - Internet-Geschwurbel. Obwohl... ;-)
- Faktorisierung: 2 x 32 x 37 = 666
- Teiler: 1, 2, 3, 6, 9, 18, 37, 74, 111, 222, 333, 666
- 666 ist eine "Dreieckszahl"
1+2+3+4+5+6+....+36 = 666 - Das Roulette wird von Abergläubischen als "Spiel des Teufels" bezeichnet, denn der Roulettekessel enthält die Zahlen von 0 bis 36. Und somit 37 Felder - womit sich der Kreis zur 37 schließt (s.o.): 666 / (6+6+6) = 37
- 666 ist eine "Smith-Zahl". Das heißt, dass die Summe der Ziffern [6+6+6] gleich der Summe der Primfaktoren ist [2+3+3+(3+7)]
- Bildet man die Summe der Quadrate der ersten sieben Primzahlen (2, 3, 5, 7, 11, 13, 17), erhält man 4 + 9 + 25 + 49 + 121 + 169 + 289 = 666
- 666 ist das Ergebnis der Summe und Differenz der Potenzen der ersten drei Zahlen: 16 - 26 + 36
- Die Summe der ersten 144 (= (6+6)²) Dezimalziffern der Kreiszahl Pi beträgt 666.
- 666 lässt sich als Summe aus Zahlen bilden, die eine Zahlenreihe von 1-9 ergeben
1 + 2 + 3 + 4 + 567 + 89 = 666
123 + 456 + 78 + 9 = 666
9 + 87 + 6 + 543 + 21 = 666 - Eine besondere Primzahl mit Bezug zur 666 ist Belphegors Primzahl mit der Nummer 1 000 000 000 000 066 600 000 000 000 001 (n=13). Sie ist an beiden Seiten von 13 aufeinanderfolgenden Nullen umgeben und von Einsen eingeschlossen. Sie hat insgesamt 31 Ziffern - der Spiegelzahl von 13.
Belphegors Primzahlen sind ein Primzahlpalindrome, bei denen die Ziffern von vorn und von hinten gelesen die gleiche Zahl ergeben. Die Zahlen haben zahlensymbolische Eigenschaften: In der Mitte steht die Zahl 666, auch "Zahl des Tieres" genannt. Links und rechts eingerahmt durch Nullen, sowie vorne und hinten durch eine 1.
Weitere "Belphegorische Primzahlen" sind 1661 (n=0) sowie die Belphegorische Primzahl (n=42) mit ingesamt 89 Stellen, davon 2*42 Nullen.
1066601 ist ebenfalls eine Belphegorische Zahl, jedoch keine Primzahl.
Die nächsten Belphegorischen Primzahlen sind (n=506), (n=608), (n=2472), (n=2623), (n=28291), (n=181298)
Belphegor ist der 7.Dämon der Hölle - Bei der Darstellung in römischen Zahlen als DCLXVI wird jeder Zahlenwert unter 1000 genau einmal verwendet, und zwar in Reihenfolge absteigender Größe
- Es lässt sich ein "Apokalyptisches Magisches Quadrat" der Kantenlänge 6 konstruieren, bei dem die Summe jeder Zeile oder Spalte UND der Diagonalen 666 beträgt. Alle Zahlen sind dabei Primzahlen. Es wird als "Apokalyptisches magisches Quadrat" bezeichnet.

- Es lässt sich ein "Magisches Quadrat" der Kantenlänge 6 konstruieren, bei dem die Summe aller eingetragenen Zahlen 666 beträgt; die Summe in jeder Zeile oder Spalte ist dabei 111
- sin (666°)+ cos [(6x6x6)°] = sin (666°)+ cos [216°] = -0,80901699437 + (-0,80901699437) = - 1,6180339887 ... was exakt der negativen Gegenzahl zur "Goldenen Zahl" φ entspricht. Die "Goldene Zahl" ist auch die "Heilige Zahl" der Mathematik, die sich in vielen Naturphänomenen, Proportionen, sowie der Kunst findet. Isn't that scary ;-)
- Phi, die "Goldene Zahl" lässt sich darstellen als
phi = -2sin(666°)
= -2cos[6×6×6)°],
phi = -[sin(666°)+cos(6×6×6)°]
= -[sin(666°)+cos(66·6)°]
= -[sin(666°)+cos(666)°]
= -[sin(666°)+cos(666666°] - Vermutlich verschlüsselte Johannes mit der Zahl 666 den Namen des römischen Kaisers Nero, der ein radikaler Christenverfolger (= der Antichrist) war. Addiert man die Zahlenwerte der hebräischen Schreibweise seines Namens "Kaiser Nero", erhält man die Zahl 666. ➜ Wikipedia: "Nimmt man die griechische Schreibweise von Kaiser Nero, Νέρων Καῖσαρ (Nerōn Kaisar), und übersetzt das auf Hebräisch, so erhält man נרון קסר (Neron Kesar). Addiert man nun die Zahlenwerte des hebräischen Alphabets, erhält man die Summe 666"
- Die Summe der ersten 144 Nachkommastellen von π ergibt 666 - die "Satanszahl" und dabei ist auch noch 144 = (6+6) x (6+6). Zum Teufel aber auch!
- Der ultimative Beweis, dass die Erde teuflisch ist wurde von Xavier Naidoo verbreitett:
Die Neigung der Erdachse beträgt 23,4°. Subtrahiert man das von 90° ergibt das... nu ... Beweis genug, verteufelt, verteufelt...?
Hier steckt der Teufel jedoch im Detail - denn Naidoo ist in seiner Weltsicht nicht nur das Komma verrutscht.
BTW: Die ➜ Neigung der Erdachse beträgt derzeit 23,43664° (23° 26′ 11.9″). Durch die Gravitationseinflüsse der anderen Körper im Sonnensystem ändert sie sich langperiodisch: sie variiert innerhalb von rund 40.000 Jahren etwa zwischen 21° 55′ und 24° 18′, also um über 2° - Xavier Naidoo bringt auch den Beweis der neuzeitlichen Verführung der Jugend durch den Teufel ins Spiel: "Friday for Future – FFF. Dreimal F. F ist am sechsten Platz im Alphabet“, sagt Naidoo und zählt die Buchstaben an seinen Fingern ab. Dann stellt er eine seltsame Verbindung her: „Dreimal F. In dem Fall 666. Da weiß man auch wieder, wer dahintersteckt.“
- Das teuflische Jahr 2020:
Multipliziert man das Jahr 2020 mit 3,3 und teilt das Ergebnis durch hundert ergibt sich 666,6 !!! Corona hat eine eindeutige Ursache! - Perfekt wird das jedoch erst durch die Zuordnung der Zahlen zu Buchstaben:
COMPUTER = 18+90+78+96+126+120+30+108 = 666
666 – das ist nach der Johannes-Offenbarung die Zahl des Tieres, des Teufels, des Bösen. Im 13. Kapitel heißt es: "Hier braucht man Weisheit. Wer Verstand hat, berechne den Zahlenwert des Tieres. Denn es ist die Zahl eines Menschennamens; seine Zahl ist sechshundertsechsundsechzig."
Computer sind des Teufels! Etzadle wissed'r des au.
- Legion's number of the first kind is defined as
L_1 = 666^(666)
= 27154..._()_(1871 digits)98016,
where 666 is the beast number. It has 1881 decimal digits.
Legion's number of the second kind is defined as
L_2 = 666!^(666!)
= 40732541..._()_(many digits)17871093760...0_()_(165·666!).
It has approximately 1.609941×10^(1596) digits, and ends with 165·666! trailing zeros. (Quelle: Wolfram Apha) - Für Mathefans sind hier noch "Evil Numbers aufgelistet: ➜ Wolfram Alpha: EvilNumber
- "Hexakosioihexekontahexaphobie" nennt man die Angst vor der Zahl 666
Verhext aber auch. - Die am ehesten einleuchtende Erklärung, weshalb diese Zahl in der Bibel auftaucht, scheint mir diese zu sein: (Quelle: sciencealert-com-watch-the-secret-meaning-behind-the-devil-s-number-666-mathematics
"When you actually look at the original text, you'll see that in this passage, the letters of 666 are actually written in Hebrew, which places a higher significance on numbers meaning words and words meaning numbers than ancient Greek. The writer was very clearly trying to tell us something.
And sure enough, if you translate the Hebrew spelling of 666, you actually spell out Neron Kesar - the Hebrew spelling of Nero Caesar. Even if you take the alternative spelling of the number of the beast, which has been found in several early Biblical texts as being written 616, you can translate that out as being Nero Cesar."
Es war eine verschlüsselte Kritik am herrschenden römischen Kaiser, der zur Zeit, als die Offenbarung geschrieben wurde, die Christen verfolgen ließ. Kein Teufelskult, .
"Durch Addition der Zahlenwerte der hebräischen Schreibweise für Kaiser Nero, נרון קסר (Neron Kesar), erhält man die Summe 666" Wikipedia - Das WWW gilt manchen als Teufelswerk, weil W = Waw der sechste Buchstabe im hebräischen Alphabet ist
- Der Koran hat 666 Suren. Die Zahl der Āyāt (Verse) im Koran beträgt 6666. Ohne die unnumerierten Basmalahs ist die Zahl der Verse im Quran 6234
- 667 - the neigbour of the Beast
- 0.666 - Number of the Millibeast
- Route 666 - Highway of the Beast
- 666°F - Oven temperature of the roast Beast
- i6686 - CPU of the Beast .
- 660 - Aproximate number of the Beast .
- Ich hau' noch einen obenauf:
Die Ordinalzahlen der Buchstaben des Wortes "Corona" lauten im Alphabet:
C=3
O=15
R=18
O=15
N=14
A=1
Die Summe ergibt 66. Die Anzahl der Buchstaben angehängt ergibt....
666
THE NUMBER OF THE BEAST !!!
BTW: Auch dies ein Netzfund ;-)
Teuflisch, teuflisch - Und heiligst unheilig:
Die Ordinalzahlen der Buchstaben des Wortes "Jesus" lauten im Alphabet:
J=10 → 10 x 9 = 90
E=5 → 5 x 9 = 45
S=19 → 19 x 9 = 171
U=21 → 21 x 9 = 189
S=19 → 19 x 9 = 171
Multipliziert man die Ordinalzahlen jeweils mit 9 und bildet die Summe ergibt das ... 666!
THE NUMBER OF THE BEAST !!!
und nun? Christ und Antichrist mit derselben Zahl?
Ist doch höllisch - Obendrauf
Die Ordinalzahlen der Buchstaben des Wortes "Messiah" ergeben - jeweils mit 9 (der auf dem Kopf stehenden Antichrist-Zahl) multipliziert, ebenfalls 666
Dasselbe funktioniert auch mit den Worten "Gospel" (Evangelium), "Cross" und "Lucifer" - Um das Ganze zu toppen:
Die Bibel hat 66 Bücher. Im 66. Buch taucht die Zahl des Tieres auf! - Nebenbei:
Heute ist der 17.5.
17+5 = 22
Die Hälfte von 22 ist 11
407 Hat die Quersumme 11
3 Jahre haben 36 Monate. So lange wird uns Corona beschäftigen.
Multipliziere ich 36 mit 407, so ergibt sich 14652.
Geteilt durch die Zahl des heutigen Tages 22 ergibt
14652:22 = .... nu... glaubt ihr es endlich? 666 !!
Mathematik lügt nicht !!! - Das ist der WISSENSCHAFTLICHE, mathematisch unwiderlegbare Beweis für die Urheberschaft von Corona! Zum Teufel aber auch! ;-) - Und noch eins für alle Impfgegner und Pharmakritiker:
Schon mal ein Kassenrezept genauer angeschaut? Links unten in der Ecke steht: "666"
Womit bewiesen ist, dass das für den Teufel ist!
Manche Leute - u.a. die Apotheker glauben jedoch, dass "666rl" das Zeichen für den Lesepunkt für das OCR-System ist, mit dem man die Rezepte digital erfassen kann.
Aber sowas ist doch sicher wieder ein Lügenmärchen und nur was für Schlafschafe. Oder für Aluhut-Verschwörungsgläubige ;-)
1729 - die Ramanujan-Zahl
- 1729 ist die kleinste Zahl, sich auf zwei verschiedene Arten als Summe zweier Kubikzahlen ausdrücken lässt: Durch die Summe von 13 + 123 oder als Summe von 93 + 103
- 1729 ist eine "sphenische Zahl", das heißt, sie ist das Produkt von genau drei Primzahlen: 1729 = 7 · 13 · 19
- 1729 ist eine "Hashad-Zahl", da sie durch die Summe ihrer Ziffern teilbar ist: 1 + 7 + 2 + 9 = 19
- Teilt man 1729 durch ihren Primfaktor 19, ergibt sich dessen Spiegelzahl 91
8128 - die vierte "perfekte" (oder "vollkommene") Zahl
- 8128 ist die Summe ihrer echten Teiler: 1, 2, 4, 8, 16, 32, 64, 127, 254, 508, 1016, 2032, 4064.
2025
- 2025 = 1³+2³+3³+4³+5³+6³+7³+8³+9³
8191
- Die Zahl 8191 ist die fünfte Mersenne-Primzahl
Im Dualsystem besteht sie aus 13 Einsen: 11111111111112
232.792.560
Die kleinste ganzzahlige Vielfache aller Zahlen von 1 bis 20 ist 232.792.560 - andersherum ausgedrückt: Diese Zahl ist durch jede Zahl zwischen 1 und 20 teilbar.Weitere "beste" Zahlen
- ➜ quora-What-is-the-best-number-mathematically
Die Zahl 142857 ist eine zyklische Zahl. Was das ist, wird hier erläutert - ➜ quora-What-are-some-really-interesting-numbers
Weitere interessante Zahlen und deren Eigenschaften - ➜ quora-What-is-your-favorite-mathematical-constant-number-Why
Weitere interessante Zahlen und deren Eigenschaften - ➜ quora-Besides-pi-what-is-a-mathematician-s-favorite-number
➜ quora-Besides-pi-what-is-a-mathematician-s-favorite-number
Weitere interessante Zahlen und deren Eigenschaften
Zehnerbündelung, 100-er Bündelung, Zahlenräume, Zahlvorstellung
Wie macht man große Zahlen anschaulich?➜ Abschnitt ansehen / wegblenden
Wie macht man große Zahlen anschaulich?
- Taschentuchpackungen. 1 Packung enthält 10 Stück
- Centstücke. 1000 cent sind 10 €
- Ohrenstäbchen, Streichhölzer, Zahnstocher mit Gummibändern bündeln
- 10er-Stäbe zu Platten / Würfeln bündeln
- Becher jeweils 100 Erbsen füllen, dann nebeneinander stellen
- Konfetti mit Klebstift auf Papier kleben
- Am 27.Juni 2019 lebten 7.714.794.469 Menschen auf der Erde
siehe ➜ dsw-org - 1.367.520.000 davon leben in China - Das sind 19⁒ der Weltbevölkerung - knapp ein Fünftel
- Die Fläche von China beträgt 9.596.960 km² - das sind 6,4⁒ der Landfläche der Erde (149.430.000 km²)
siehe ➜ welt-in-zahlen-laendervergleich
Zum Vergleich:
In 0,3 Kubikmeter Humus (das entspricht einer Fläche von 1x1 Meter und 30 cm Tiefe) leben 1,6 Billionen Lebewesen - 1000mal soviel wie Menschen in China - Update der Weltbevölkerung am 30.10.2024:
Nach Berechnungen der Vereinten Nationen (UN) erreichte die Weltbevölkerung Mitte 2024 fast 8,2 Milliarden Menschen. Damit hat sich die Zahl der Menschen seit Mitte der siebziger Jahre verdoppelt. Damals lebten rund vier Milliarden Menschen auf der Erde. 1950 waren es noch 2,5 Milliarden Menschen.
Am 1. Juli 2024 zählte die UN 8,16 Milliarden Menschen auf der Erde. Mehr als die Hälfte aller Menschen lebte in Asien, weniger als jede/-r Zehnte in Europa.
Quelle: ➜ destatis
Mengenvorstellung / Zahlvorstellung
- 1000 Büroklammern aneinander hängen lassen und als Kette aufhängen. 20 Schüler à 50 Stück = 1000
- Eine Rolle Klopapier hat 200 Blatt. 5 Rollen im Flur ausrollen = 1000 Blatt
- Im Sitzkreis Erbsen zählen. Jeweils 10 bündeln zu 100
- Reiskörner: Löffel mit 10, Schnapsglas mit 100.
- Millimeterpapier. Mehrere Bögen. 10 färben, 100 färben, 1000 färben... 10x10 cm geben schon 10.000
- Zählwaage. Nach meiner Waage wiegen 70 Popkorn-Maiskörner 70 Gramm. In einer Packung mit 500 Gramm befinden sich somit etwa 500 Maiskörner.
10.000 Maiskörner sind damit 10 Kilo. Das gibt eine MENGE Popkorn ;-) - In einer Packung Tackerklammern befinden sich in der Regel 1000 Stück
- Eine Packung Spanplattenschrauben enthält 600 Stück - je nach Größe
- Wenn ein Teppich auf 10 Zentimeter 40 Knoten aufweist, ergibt das auf 50 Reihen - also auf 1 dm² 2000 Knoten.
Ein Kind, das in Indien einen Teppich webt, hat für einen Teppich im Format 2 x 3 Meter für uns (20x30=6000 dm²) = 12.000.000 Knoten geknüpft
Zahlworte mit tausend
tausenderlei, tausendäugig, Tausendbein, Tausendfüßler, tausendbeinig, Tausendblatt, tausendblättrig, Tausendblume, Tausende, Tausendeck, Tausendengel, Tausendschatz, Tausender, Tausenderlei, tausendfach, tausendfältig, tausendfaltig, tausendfarben, tausendfarbig, tausendförmig, Tausendfreude, tausendfündig, Tausendfunke, Tausendfuß, Tausendgeblitze, Tausendglück, Tausendguldenkraut, tausendgut, Tausendhändel, tausendhändig, tausendjährig, tausendkehlig, Tausendkind, tausendköpfig, Tausendkunst, Tausendkünster, Tausendkünstlerin, Tausendkünstiger, Tausendkünstler, tausendkünstig, Tausendkünstlerei, tausendkünstlerisch, tausendlistig, Tausendlistiger, Tausendlügner, Tausendlust, tausendmal, tausendmalig, tausendmeilig, Tausendmeister, tausendnamig, tausendoft, tausendpfündig, tausendquellig, Tausendsassa, tausendsäulig, Tausendschaft, Tausendschatz, Tausendschelm, Tausendschläfer, tausendschneidig, tausendschön, Tausendschön, Tausendschönchen, Tausendskerl, Tausendskind, tausendslieb, Tausendslust, Tausendspaß, tausendste, tausendstel, tausendstimmig, Tausendtalermann, Tausendteil, tausendtönig, Tausendtränenguß, tausendviel, Tausendvogel, tausendweis, tausendweisig, tausendzählig, tausendzüngigPotenzen + große Zahlen
Das Wunder des Lebens - eine Zweierpotenz➜ Abschnitt ansehen / wegblenden
Das Wunder der Gesundheit - Hahnemann und die Potenzen
Zur Herstellung von Globuli mit der Potenz D 30 wird die Ausgangssubstanz 1:1.000.000.000.000.000.000.000.000.000.000 (in Worten: eine Quintillion) =10 30 verdünnt.1 m³= 1.000 Liter = 1.000.000 ml
Der Tender der Dampflokomotiven-Baureihe B 01 fasst 34.000 Liter, also 34.000.000 ml.
Wenn ich 1 ml Ausgangssubstanz mit D30 potenziere - und nichts wegschütte - kann ich damit 2,941176471×1022 Dampflokomotiven füllen, die dann - nach Hahnemanns Vorstellung - mit höherer Geschwindigkeit und weniger Verschleiß laufen.
Maithink zum Thema Homöopa-Tea:
➜ youtube
Kommentare von dieser Seite:
"Woher bekommen die Hersteller überhaupt das "feinstofflich saubere" Wasser, mit dem sie den Wirkstoff dann verdünnen? Jedes Wasser auf der Welt ist doch bereits von allem "informiert", mit dem es jemals in Kontakt gekommen ist, in den Milliarden Jahren, die es die Welt gibt also so ziemlich mit allem. Kann Wasser also doch vergessen? Und wie bringen die Hersteller es dazu?"
"Wer einmal in einer Kläranlage war, will nicht das Wasser ein Gedächtnis hat, absolut nicht."
"Jetzt weiss ich auch, warum Bond seinen Martini immer geschüttelt und nicht gerührt haben will. Das ballert einfach viel mehr rein."
Das Magazin Neo Royale hat dem Thema ebenfalls eine Sendung gewidmet:
➜ youtube
Wikipedia zur Homöopathie
Beispielverdünnungen siehe ➜ Wikipedia - PotenzierenPotenztabelle
| Potenz | Bezeichnung | Kürzel | Maß | Bemerkungen |
|---|---|---|---|---|
| 1030 | Quetta | Q | Cinquillionen | |
| 1027 | Ronna | R | Quadrilliarden | |
| 1024 | Yotta | Y | Quadrillionen | ≈ 100 Mio. Lj |
| 1021 | Zetta | Z | Trilliarden | 1,9 Zm (0,2 Mio. Lj) – Durchmesser der Milchstraße |
| 1018 | Exa | E | Trillionen | griech. exa: über alles |
| 1015 | Peta | P | Billiarden | griech. petanünnein: alles umfassen |
| 1012 | Tera | T | Billionen | griech. teras: ungeheuer groß |
| 109 | Giga | G | Milliarden | griech. gigas: riesige Zahl |
| 106 | Mega | M | Millionen | griech. megas: große Zahl |
| 103 | Kilo | K | Tausend | griech chilioi: tausend |
| 102 | Hekto | Hundert | gr. hekaton: hundert | |
| 101 | Deka | Zehn | gr. deka: zehn | |
| 10-1 | Dezi | d | Zehntel | lat. decem: zehn |
| 10-2 | Zenti | c | Hundertstel | lat. centum: hundert |
| 10-3 | Milli | m | Tausendstel | lat. millesimus: der tausendste Teil |
| 10-6 | Mikro | µ | Millionstel | griech. mikros: klein, unbedeutend |
| 10-9 | Nano | n | Milliardstel | griech. nanos: zwerghaft klein |
| 10-12 | Piko | p | Billionstel | ital. pico: sehr klein |
| 10-15 | Femto | f | Billiardstel | dän.-norw. femten: 15 |
| 10-18 | Atto | a | Trillionstel | dän.-norw. atten: 18 |
| 10-21 | Zepto | z | ||
| 10-24 | Yocto | y | ||
| 10-27 | Ronto | r | ||
| 10-30 | Qekto | q | ||
| 10-33 | Vunkto | v | ||
| 10-36 | Unto | u |
Binärsystem - Zweierpotenzen
Ein paar mathematische Gedankenspiele zur 2-er-Potenz:- Nimmt man ein normales DIN-A-4-Blatt und faltet es, wird es doppelt so dick. Logisch. Faltet man es nochmal, ist es vier Mal so dick wie das Ursprungspapier. Kein Blatt Papier, egal wie groß, kann mehr als 9 Mal gefaltet werden. Das dürft ihr gerne ausprobieren
- Wie oft müsste man (Standard-)Schreibmaschinenpapier falten, damit es so dick wäre, damit der gefaltete Stapel die Distanz zum Mond überbrücken würde?
Die Antwort lautet - und man verneige sich vor Douglas Edams - 42.
0,1 mm x 2⁴² ergibt etwa 300.000 km - nach 42maligem Falten (was technisch nur im Gedankenexperiment möglich ist), hätte man die Entfernung zum Mond erreicht - Nach fünfzigmaligem Falten eines Papieres (250) würde sich ein Papierberg ergeben, der eine Höhe von mehr als hundert Millionen Kilometern hat
- Könnte man ein Zeitungspapier 100 Mal falten, wäre der Stapel dicker als das ganze bekannte Universum
- siehe dazu auch: ➜ Quelle: besserwisserseite.de/statistik.phtml
- Das faszinierendste Beispiel für 2-er-und 10-er-Potenzen ist der Mensch.
Wie viele Körperzellen stehen am Beginn eines menschlichen Lebens? - Klar. Zwei. Eine Ei- und eine Samenzelle.
Diese verschmelzen ihre jeweils 23 Chromosomen zu 46 Chromosomenpaaren und dann beginnt die Teilung. Die Zellen teilen sich, spezialisieren sich dabei und "wissen" genau, an welche Stelle des Organismus sie sich spezialisieren müssen, damit am Ende ein Mensch aus ca. 7x1013 Körperzellen entsteht, der sich mit Vorliebe der Mathematik widmet.
Ein Teil dieser 70 Billionen Körperzellen stirbt täglich ab und erneuert sich täglich. So "tauschen" wir Menschen unsere Haut ca. 1-mal pro Monat komplett aus, die Knochen alle 10 Jahre.
Die DNA in den 46 Chromosomen einer einzigen Zelle ergibt auseinander gezogen eine Länge von ca. 2 Meter, die jedoch nur nur winzige zwei Nanometer (2x10-9 Meter) im Durchmesser aufweist. Aneinandergereiht ergäbe die gesamte DNA eines Menschen eine Entfernung von 140 Billionen Meter, also 140 Milliarden Kilometer. Die Entfernung Erde-Sonne beträgt 140 Millionen Kilometer. Man könnte also mit der DNA eines einzigen Menschen diese Entfernung 500 mal hin- und zurück spannen.
Seit dem Jahr 2003 wissen die Forscher, wieviele Eiweiß-Bausteine insgesamt auf dem zwei Meter langen DNA-Faden des Menschen Platz haben: Es sind 3,2 Milliarden (=3,2 x 109 Bausteine pro Körperzelle.
Wunder Mensch - oder besser gesagt: Wunder Leben. In einer Zwiebelzelle befinden sich nur 7 Chromosomen, die auch etwas kürzere DNA-Stränge aufweisen. Aber auch hier ergeben sich rasch gigantische Dimensionen - Die Geschichte des Schachbretts und die Dynamik der 2-er-Potenz. Der Erfinder des Schachbretts wollte - als er nach dem Lohn für sein Spiel gefragt wurde, nur für jedes Feld des Schachbretts das Doppelte des vorherigen Feldes. Der Herrscher beherrschte keine Mathematik, sonst hätte er bemerkt, dass dieser Lohn die gesamte Jahresproduktion der Erde um das 1200-fache überstiegen hätte. 1-2-4-8...264 Reiskörner, die zudem aufaddiert werden.
ergeben 18.446.744.073.709.551.615 Reiskörner - ca. 18,5 Trilliarden Körner mit einer Gesamtmasse von ca. 730 Mrd Tonnen.
siehe auch ➜ de-wikipedia-org-wiki-Sissa_ibn_Dahir
Wikipedia: Sissa ibn Dahir (auch: Sessa) lebte angeblich im dritten oder vierten Jahrhundert n. Chr. in Indien und gilt Legenden zufolge als der Erfinder des Schachspiels
Riesige Zahlen
- Um unvorstellbar große Zahlen notieren zu können, wird die siehe auch ➜ Wikipedia: Steinhaus-Moser-Notation verwendet
- Die größte in einem mathematischen Beweis verwendete Zahl war laut dem Guiness-Buch der Rekorde siehe auch ➜ Wikipedia: Grahams_Zahl. Wie alle Rekorde wurde auch dieser "Rekord" schon längst gebrochen
- Eine Unendlichkeitsmaschine ist eine Getriebekonstruktion, die bereits von Leonardo da Vinci skizziert wurde. Die Maschine veranschaulicht durch mehrfache Getriebeuntersetzung die fortschreitende Bewegungslosigkeit der beteiligten, immer langsamer laufenden Zahnräder. Es scheint, dass eine solche Maschine ewig laufen könnte. Unendlichkeitsmaschinen stehen in vielen Technikmuseen. Die Maschine kann mit Zahnrädern oder Schneckengetrieben gebaut werden.
Die Unendlichkeitsmaschine besitzt ein 16-stufiges Untersetzungsgetriebe mit jeweils gleichen Getriebesätzen. Der Getriebeeingang wird mit konstanter Geschwindigkeit gut wahrnehmbar angetrieben. Der Getriebeausgang ist einbetoniert.
Paradox erscheint, dass der Getriebeeingang ohne Unterlass angetrieben wird, während der einbetonierte Getriebeausgang offensichtlich sich überhaupt nicht drehen kann. Dies lässt sich damit erklären, dass die "verloren gegangene Bewegung" hauptsächlich durch Spiel im Getriebe erzeugt wird. Bei dem Exemplar im Dynamikum dreht sich der Ausgang einer Stufe mit einem Siebtel der Geschwindigkeit des Eingangs.
Durch die Hintereinanderschaltung von 16 Stufen potenziert sich die Untersetzung zu 716 = 33.232.930.569.601. Dreht sich z. B. das Zahnrad des Getriebeeingangs einmal pro Sekunde, ergibt die Gesamtheit der Untersetzungen, dass das Zahnrad des Getriebeausgangs etwa eine Million Jahre für eine Umdrehung benötigen würde, wäre dies nicht einbetoniert.
zitiert aus
➜ de-wikipedia-org-wiki-Unendlichkeitsmaschine
Googol
- 1938 bat der amerikanische Mathematiker Edward Kasner seinen neunjährigen Neffen Milton Sirotta, sich einen Namen für die Zahl 10 hoch 100 auszudenken. Dieser schlug "Googol" vor. Als viele Jahre später zwei junge Programmierer einen Namen für ihre Suchmaschine suchten, dachten sie an die riesige Menge der Internetseiten, die sie erfassen wollten. Der Rest ist Geschichte .
- ➜ wikipedia:googol
- Die Zahl »Googolplex« (10 hoch 10 hoch 100) auszuschreiben ist unmöglich! Selbst alle Materieteilchen des bisher sichtbaren Universums würden nicht ausreichen die Zahl darzustellen..wikipedia:googol
Mein kostenloses Online-Werkstattbuch zu "fast vergessenen" künstlerischen Techniken.
Wie? Gratis? Ja. Gratis! Kunst trifft Alchemie & Weiterbildung.
Frohes Stöbern!
180 Seiten gratis online. Erhältlich auch als Buch mit 232 A4-Seiten. Und MEHR Input ;-) ISBN 978-3-9821765-0-5
Tipps für Tiefdruck, Flachdruck, analoge Fotografie, Cyanotypie, Farbherstellung, Papier schöpfen, Galvanik, Kunstgeschichte ... ein weites Feld ...
Kleine Zahlen, negative Potenzen
Die Sache mit den Genen➜ Abschnitt ansehen / wegblenden
❱21❱ ➜
biotechlerncenter.interpharma.ch/themen/gentechnik/
Zellen und Gene: "Der Körper eines Menschen besteht aus Milliarden von Zellen. Zellen sind die kleinsten lebenden Einheiten des Körpers, sie sind 10 bis 100 Mikrometer gross (1 Mikrometer entspricht 10-6 Meter bzw. einem Millionstel Meter), von Auge sind sie also nicht mehr erkennbar. ... Würde man alle 46 DNA-Fäden, welche in einem Zellkern auf die Chromosomen verteilt sind, aneinander reihen, dann wäre dieser Faden zwei Meter lang, aber nur winzige zwei Nanometer (2x10-9 Meter) im Durchmesser." Seit dem Jahr 2003 wissen wir jedoch, dass es maximal 25'000 Gene sind. Zum Vergleich: Das Darmbakterium Escherichia coli besitzt 4'500 Gene, der Fadenwurm Caenorhabditis elegans etwa 19'000. Fast gleichviel Gene wie der Mensch besitzt die Pflanze Ackerschmalwand Arabidopsis thaliana mit 25'500 Genen"
❱21❱ ➜ learn-genetics-utah-edu-content-cells-scale
Cell Size and Scale - Über den Schieberegler kann man das "Mikroskop" benutzen und immer weiter in die Welt der kleinen Bestandteile eintauchen. Interessant dabei: Der Kopf eines Spermiums ist so groß wie das X-Chromosom - weil er fast nur daraus besteht. Man taucht immer weiter in die Welt des Kleinen - bis zum Kohlenstoffatom mit einem Durchmesser von 340 Picometer.
Zellen und Gene: "Der Körper eines Menschen besteht aus Milliarden von Zellen. Zellen sind die kleinsten lebenden Einheiten des Körpers, sie sind 10 bis 100 Mikrometer gross (1 Mikrometer entspricht 10-6 Meter bzw. einem Millionstel Meter), von Auge sind sie also nicht mehr erkennbar. ... Würde man alle 46 DNA-Fäden, welche in einem Zellkern auf die Chromosomen verteilt sind, aneinander reihen, dann wäre dieser Faden zwei Meter lang, aber nur winzige zwei Nanometer (2x10-9 Meter) im Durchmesser." Seit dem Jahr 2003 wissen wir jedoch, dass es maximal 25'000 Gene sind. Zum Vergleich: Das Darmbakterium Escherichia coli besitzt 4'500 Gene, der Fadenwurm Caenorhabditis elegans etwa 19'000. Fast gleichviel Gene wie der Mensch besitzt die Pflanze Ackerschmalwand Arabidopsis thaliana mit 25'500 Genen"
❱21❱ ➜ learn-genetics-utah-edu-content-cells-scale
Cell Size and Scale - Über den Schieberegler kann man das "Mikroskop" benutzen und immer weiter in die Welt der kleinen Bestandteile eintauchen. Interessant dabei: Der Kopf eines Spermiums ist so groß wie das X-Chromosom - weil er fast nur daraus besteht. Man taucht immer weiter in die Welt des Kleinen - bis zum Kohlenstoffatom mit einem Durchmesser von 340 Picometer.
Kunst + Mathematik
Die Fibonacci-Reihe, Goldene Zahlen und der "Goldene Schnitt"➜ Abschnitt ansehen / wegblenden
Faszinierende Natur - und faszinierende Mathematik: Weshalb Ananas, Kakteen, Tannenzapfen und viele andere Pflanzen etwas mit den Fibonacci-Zahlen gemein haben - und wie die Fibonacci-Zahlen wiederum mit der Goldenen Zahl zusammenhängen.
Die Fibonacci-Reihe entwickelte Fibonacci aus dem Gedankenmodell der Kaninchenvermehrung. Am Anfang gibt es 1 Paar. Die Regel lautet nun: Jedes neu geborene Paar braucht einen Monat, bis es geschlechtsreif ist und Nachkommen zeugen kann. Von da an gebieren nun die geschlechtsreifen Paare jeden Monat ein neues Paar Kaninchen. Weitere Regel: Keines dieser mathematischen Gedanken-Kaninchen stirbt. Wie viele Paare sind dann in jeder der folgenden Generationen vorhanden?
Lösung: Zu jedem Paar einer Generation kommen genau so viele neugeborene Paare hinzu, wie im Vormonat vorhanden waren.
Fibonacci-Zahlen ergeben somit die Folge
1,1,2,3,5,8,13,21,34 ...
(1+1=2), (2+1=3), (3+2=5), (5+3=8) ....
Teilt man in der Fibonacci-Reihe die Nachfolger- durch die Vorgängerzahl, so nähert sich der Quotient (je größer die Zahlen werden) immer näher der Goldenen Zahl 1,61803398... an, diese wiederrum ist, wenn man daraus den Kehrbruch bildet, genau um 1 kleiner und hat die Zahlenfolge: 0,61803398... Dies gilt NUR für diese Zahl. Die Goldene Zahl ist zudem die einzige Zahl, die sich aus einer mathematischen Regel bilden lässt, die ausschließlich aus 1sen und Rechenzeichen besteht (ohne Kombinationen wie 11 oder 111 ... zu verwenden)
An vielen Pflanzen lassen sich die Fibonacci-Zahlen, die goldene Zahl und der goldene Winkel ablesen. Auch das "magische" Pentagramm besitzt in der Diagonale die Goldene Zahl als Streckenverhältnis - und kommt in vielen Pflanzen vor - unter anderem im Kerngehäuse von Äpfeln.
Galileo Galilei meinte:
"Das Buch der Natur ist in Mathematik geschrieben."
Die Fibonacci-Reihe entwickelte Fibonacci aus dem Gedankenmodell der Kaninchenvermehrung. Am Anfang gibt es 1 Paar. Die Regel lautet nun: Jedes neu geborene Paar braucht einen Monat, bis es geschlechtsreif ist und Nachkommen zeugen kann. Von da an gebieren nun die geschlechtsreifen Paare jeden Monat ein neues Paar Kaninchen. Weitere Regel: Keines dieser mathematischen Gedanken-Kaninchen stirbt. Wie viele Paare sind dann in jeder der folgenden Generationen vorhanden?
Lösung: Zu jedem Paar einer Generation kommen genau so viele neugeborene Paare hinzu, wie im Vormonat vorhanden waren.
Fibonacci-Zahlen ergeben somit die Folge
1,1,2,3,5,8,13,21,34 ...
(1+1=2), (2+1=3), (3+2=5), (5+3=8) ....
Teilt man in der Fibonacci-Reihe die Nachfolger- durch die Vorgängerzahl, so nähert sich der Quotient (je größer die Zahlen werden) immer näher der Goldenen Zahl 1,61803398... an, diese wiederrum ist, wenn man daraus den Kehrbruch bildet, genau um 1 kleiner und hat die Zahlenfolge: 0,61803398... Dies gilt NUR für diese Zahl. Die Goldene Zahl ist zudem die einzige Zahl, die sich aus einer mathematischen Regel bilden lässt, die ausschließlich aus 1sen und Rechenzeichen besteht (ohne Kombinationen wie 11 oder 111 ... zu verwenden)
An vielen Pflanzen lassen sich die Fibonacci-Zahlen, die goldene Zahl und der goldene Winkel ablesen. Auch das "magische" Pentagramm besitzt in der Diagonale die Goldene Zahl als Streckenverhältnis - und kommt in vielen Pflanzen vor - unter anderem im Kerngehäuse von Äpfeln.
Galileo Galilei meinte:
"Das Buch der Natur ist in Mathematik geschrieben."
❱21❱ ➜
boersenlexikon-faz-net-definition-fibonacci-zahlen
Zitat aus dem (online-)Börsenlexikon der FAZ:
"Fibonacci-Zahlen
Eine unendliche Zahlenreihe, die mit 0 und 1 beginnt. Jede weitere Zahl entspricht dabei der Summe der beiden vorangegangenen Zahlen. Damit lautet der Anfang der Zahlenreihe 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 usw. Der Quotient von zwei aufeinanderfolgenden Zahlen (z.B. 55 und 89) läuft immer mehr gegen 0,618, je höher die Zahlen werden. Der Quotient aus einer Zahl und der jeweils übernächsten (z.B. 21 und 55) nähert sich dabei immer mehr 0,382 an. Diese beiden Quotienten 0,618 und 0,382 werden häufig benutzt, um das Korrekturpotential nach vorausgegangenen Kursbewegungen zu bestimmen. Die Theorie stützt sich darauf, dass bei Gegenbewegungen häufig Widerstands- oder Unterstützungslinien zu beobachten sind, an denen die Kursbewegung vergleichsweise häufiger zum Stehen kommt. Diese Linien (Retracments) können durch Fibonacci-Verhältnisse häufig mit hoher Genauigkeit bestimmt werden."
❱24Q2❱ ➜ r-knott-surrey-ac-uk-Fibonacci-fib
Fibonacci-Zahlen und die "Goldenen Zahlen" - Startseite mit Links
❱24Q2❱ ➜ r-knott-surrey-ac-uk-Fibonacci-phi2DGeomTrig
Fibonacci-Zahlen und die "Goldenen Zahlen"
❱24Q2❱ ➜ r-knott-surrey-ac-uk-Fibonacci-phi
Fibonacci-Zahlen und die "Goldenen Zahlen"
❱24Q2❱ ➜ r-knott-surrey-ac-uk-Fibonacci-fibnat
für Biologen und "Wunderer" - Fibonacci-Zahlen in der Natur
❱21❱ ➜ mathe-seiten.de/fibonacci
für abgedrehte Mathematiker-Hirne: Rechnungen mit Fibonacci-Zahlen
❱21❱ ➜ archive-org-spasslernen.de/spiele/denk28 (längere Ladezeit, da aus archive-org eingebunden)
Hexen, Kaninchen und die Zahlen des Signore Fibonacci

"Experimentelle Zufallswahrscheinlichkeit im Goldenen Schnitt"
Geometrische Konstruktion im goldenen Verhältnis, Farbverteilung durch Auswürfeln der Farbfelder.
Acryl auf Leinwand, 70 x 100 cm, © Wolfgang Autenrieth, 2019 - "Bauhausjahr"
Der Goldene Schnitt - 13 Seiten PDF (Mathematische Facharbeit)... mit ziemlich fiesen Formeln ;-) Bemerkenswert ist jedoch die Konstruktion des Goldenen Schnitts aus Quadraten mit Fibanocci-Zahlen.
❱21❱ ➜ members.chello.at/gut.jutta.gerhard/golds
Der Goldene Schnitt
❱21❱ ➜ mathematische-basteleien.de/goldenerschnitt
Der Goldene Schnitt - mathematisch betrachtet. mit Linkverweisen
❱21❱ ➜ nanopdf.com/download/4-die-fibonacci_pdf
Die Fibonacci-Zahlen und der Goldene Schnitt - mit Abbildungen (6S. PDF)
❱23Q2❱ ➜ schule-bw.de-faecher-und-schularten-mathematik-unterrichtsmaterialien-besondere-zahlen-goldener-schnitt
Verschiedene Lernumgebungen zum "Goldenen Schnitt"
❱23Q2❱ ➜ schule-bw-de-mathematik-unterrichtsmaterialien-goldener-schnitt-pentagramm
Der Goldene Schnitt im Pentagramm - dem Zeichen der Freimaurer
❱21❱ ➜ spektrum-kolumne-silberner-schnitt-und-plastikzahl
Neben dem "Goldenen Schnitt" gibt es auch den "Silbernen Schnitt", den kupfernen und sogar die "Plastikzahl"
Goldener Schnitt im Anthrowiki
❱21❱ ➜ commons-wikimedia-org-wiki-Category:Golden_ratio
Abbildungen zum Goldenen Schnitt auf Commons
❱21❱ ➜ de-wikipedia-org-wiki-Goldener_Schnitt
Wikipedia
❱21❱ ➜ Wikipedia: Harmonische Teilung
❱21❱ ➜ Wikipedia: Silberner Schnitt
youtube: Mathematik zum Anfassen - Der goldene Schnitt am Fünfeck gezeigt: Als Streckenteilung im Verhältnis von 62% zu 38 %.
❱21❱ ➜ youtube-com-watch?v=LDoKsw3SOdw
Der goldene Schnitt und die Fibonacci-Folge (Weitz)
❱21❱ ➜ youtube-com-watch?v=MyVaGOEt6MQ
Der Goldene Schnitt und sein Vorkommen in der heutigen Welt | Besondere Zahlen in der Natur
Zitat aus dem (online-)Börsenlexikon der FAZ:
"Fibonacci-Zahlen
Eine unendliche Zahlenreihe, die mit 0 und 1 beginnt. Jede weitere Zahl entspricht dabei der Summe der beiden vorangegangenen Zahlen. Damit lautet der Anfang der Zahlenreihe 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 usw. Der Quotient von zwei aufeinanderfolgenden Zahlen (z.B. 55 und 89) läuft immer mehr gegen 0,618, je höher die Zahlen werden. Der Quotient aus einer Zahl und der jeweils übernächsten (z.B. 21 und 55) nähert sich dabei immer mehr 0,382 an. Diese beiden Quotienten 0,618 und 0,382 werden häufig benutzt, um das Korrekturpotential nach vorausgegangenen Kursbewegungen zu bestimmen. Die Theorie stützt sich darauf, dass bei Gegenbewegungen häufig Widerstands- oder Unterstützungslinien zu beobachten sind, an denen die Kursbewegung vergleichsweise häufiger zum Stehen kommt. Diese Linien (Retracments) können durch Fibonacci-Verhältnisse häufig mit hoher Genauigkeit bestimmt werden."
❱24Q2❱ ➜ r-knott-surrey-ac-uk-Fibonacci-fib
Fibonacci-Zahlen und die "Goldenen Zahlen" - Startseite mit Links
❱24Q2❱ ➜ r-knott-surrey-ac-uk-Fibonacci-phi2DGeomTrig
Fibonacci-Zahlen und die "Goldenen Zahlen"
❱24Q2❱ ➜ r-knott-surrey-ac-uk-Fibonacci-phi
Fibonacci-Zahlen und die "Goldenen Zahlen"
❱24Q2❱ ➜ r-knott-surrey-ac-uk-Fibonacci-fibnat
für Biologen und "Wunderer" - Fibonacci-Zahlen in der Natur
❱21❱ ➜ mathe-seiten.de/fibonacci
für abgedrehte Mathematiker-Hirne: Rechnungen mit Fibonacci-Zahlen
❱21❱ ➜ archive-org-spasslernen.de/spiele/denk28 (längere Ladezeit, da aus archive-org eingebunden)
Hexen, Kaninchen und die Zahlen des Signore Fibonacci
Der Goldene Schnitt - Mathematik für Künstler
"Goldenes Verhältnis" (ratio aurea) oder "Goldener Schnitt" (sectio aurea)- Mathematische Bedingung
(M+m) / M = M / m
Ein Punkt teilt eine Strecke im Goldenen Schnitt, wenn der Quotient aus der Summe der Teilstrecken und der längeren Teilstrecke dem Quotienten aus der längeren und der kürzeren Strecke entspricht - Irrationaler Zahlenwert
φ = (1 + √5) / 2 ≈ 1,618 - Spiegelzahl
Wird mit der goldenen Zahl 1,61803398... der Kehrbruch gebildet, so ist 1 / 1,61803398... = 0,61803398... Es ändert sich somit nur der ganzzahlige Anteil von 1 auf 0 - Einserzahl
Die goldene Zahl ist die einzige Zahl, die sich nur aus 1'en darstellen lässt - als Kettenbruch:
φ = 1 + 1/(1+(1/(1+(1/1+(1/(1+(1/(1+(1/1+. - φ2, φ3, φ4,
Der Goldene Schnitt φ ist die positive Lösung der Gleichung x2−x−1=0
Es ergibt sich daraus: φ2=φ+1. Um φ zu quadrieren, muss man nur 1 zu φ addieren.
φ3=φ·φ2=φ·(φ+1)=φ2+φ=2φ+1
φ4=φ·φ3=φ·(2φ+1)=2φ2+φ=2(φ+1)+φ=3φ+2
φ2−φ=1
φ3−φ2=φ
φ4−φ3=φ+1=φ2
Allgemein: φn=φ(n−1)+φ(n−2) - Zusammenhang zu Fibonacci-Zahlen
Teilt man in der Fibonacci-Reihe die Nachfolger- durch die Vorgängerzahl, so nähert sich der Quotient (je größer die Zahlen werden) immer näher der Goldenen Zahl - Phi, die "Goldene Zahl" lässt sich darstellen als
phi = -2sin(666°)
= -2cos[6×6×6)°],
phi = -[sin(666°)+cos(6×6×6)°]
= -[sin(666°)+cos(66·6)°]
= -[sin(666°)+cos(666)°]
= -[sin(666°)+cos(666666°]
... zum Teufel aber auch ;-) - Faszinierendes
Der Bauchnabel eines Menschen teilt die Körperhöhe eines Menschen in der Regel genau im Goldenen Schnitt
Die Oberarmlänge verhält sich zur Unterarmlämge im Verhältnis 1:1,62
Die Länge des oberen Fingergliedes verhält sich zur Länge des unteren Fingergliedes im Verhältnis 1:1,62 - Der goldene Zirkel
siehe auch ➜ archive.org: uni-hildesheim-de-~stegmann-goldschn-pdf
Abhandlung zum Goldenen Schnitt (42 S. PDF). Interessant darin die Anleitung zum Bau eines "Goldenen-Schnitt-Zirkels" - φ ist das Ergebnis einer verschachtelten Quadratwurzelfolge:
\( \sqrt{2+\sqrt{2-\sqrt{2+\sqrt{2-\cdots}}}} = \varphi \)

"Experimentelle Zufallswahrscheinlichkeit im Goldenen Schnitt"
Geometrische Konstruktion im goldenen Verhältnis, Farbverteilung durch Auswürfeln der Farbfelder.
Acryl auf Leinwand, 70 x 100 cm, © Wolfgang Autenrieth, 2019 - "Bauhausjahr"
Linktipps zum "Goldenen Schnitt"
❱21❱ ➜ chorgiessen-goldfibo-pdfDer Goldene Schnitt - 13 Seiten PDF (Mathematische Facharbeit)... mit ziemlich fiesen Formeln ;-) Bemerkenswert ist jedoch die Konstruktion des Goldenen Schnitts aus Quadraten mit Fibanocci-Zahlen.
❱21❱ ➜ members.chello.at/gut.jutta.gerhard/golds
Der Goldene Schnitt
❱21❱ ➜ mathematische-basteleien.de/goldenerschnitt
Der Goldene Schnitt - mathematisch betrachtet. mit Linkverweisen
❱21❱ ➜ nanopdf.com/download/4-die-fibonacci_pdf
Die Fibonacci-Zahlen und der Goldene Schnitt - mit Abbildungen (6S. PDF)
❱23Q2❱ ➜ schule-bw.de-faecher-und-schularten-mathematik-unterrichtsmaterialien-besondere-zahlen-goldener-schnitt
Verschiedene Lernumgebungen zum "Goldenen Schnitt"
❱23Q2❱ ➜ schule-bw-de-mathematik-unterrichtsmaterialien-goldener-schnitt-pentagramm
Der Goldene Schnitt im Pentagramm - dem Zeichen der Freimaurer
❱21❱ ➜ spektrum-kolumne-silberner-schnitt-und-plastikzahl
Neben dem "Goldenen Schnitt" gibt es auch den "Silbernen Schnitt", den kupfernen und sogar die "Plastikzahl"
Wikipedia
❱21❱ ➜ anthrowiki-Goldener_SchnittGoldener Schnitt im Anthrowiki
❱21❱ ➜ commons-wikimedia-org-wiki-Category:Golden_ratio
Abbildungen zum Goldenen Schnitt auf Commons
❱21❱ ➜ de-wikipedia-org-wiki-Goldener_Schnitt
Wikipedia
❱21❱ ➜ Wikipedia: Harmonische Teilung
❱21❱ ➜ Wikipedia: Silberner Schnitt
Videos
❱21❱ ➜ youtube-com-watch?v=-Pg35JJCUH8youtube: Mathematik zum Anfassen - Der goldene Schnitt am Fünfeck gezeigt: Als Streckenteilung im Verhältnis von 62% zu 38 %.
❱21❱ ➜ youtube-com-watch?v=LDoKsw3SOdw
Der goldene Schnitt und die Fibonacci-Folge (Weitz)
❱21❱ ➜ youtube-com-watch?v=MyVaGOEt6MQ
Der Goldene Schnitt und sein Vorkommen in der heutigen Welt | Besondere Zahlen in der Natur
Fraktale
Mathematik trifft Kunst und Unendlichkeit➜ Abschnitt ansehen / wegblenden
❱22Q4❱ ➜
spektrum-de-video-wie-selbstaehnlich-ist-unser-universum
Seit vielen Jahren bin ich von Fraktalen fasziniert. Nun gibt es einen Beitrag auf Spektrum der Wissenschaft, in dem es um die Selbstähnlichkeit von Strukturen in galaktischem Ausmaß geht. Auch Spock fände das faszinierend. Vielleicht auch eure Schüler - zumal das über mathematische Formeln nachgewiesen wurde.
Spezialisiert ist das Programm auf dreidimensionale Fraktale wie Mandelbulb, Mandelbox oder IFS, jedoch lassen sich auch Fraktale anderer Dimensionen visualisieren und rendern. M
Iterierendes Funktionensystem
❱22Q4❱ ➜ de-wikipedia-org-wiki-Kategorie: Fraktale-Geometrie
Kategorie Fraktale Geometrie
❱22Q4❱ ➜ de-wikipedia-org-wiki-Julia-Menge
Julia-Menge
❱22Q4❱ ➜ de-wikipedia-org-wiki-Fraktalgenerator
Wikipedia-Eintrag: "Fraktalgenerator"
❱22Q4❱ ➜ de-wikipedia.org-wiki-Lindenmayer-System
Lindenmayer-System - ein Formelsystem, das den Getreiden ähnliche Strukturen erzeugt
❱22Q4❱ ➜ de-wikipedia.org-wiki-Mandelbrot-Menge
Mandelbrot-Menge
Seit vielen Jahren bin ich von Fraktalen fasziniert. Nun gibt es einen Beitrag auf Spektrum der Wissenschaft, in dem es um die Selbstähnlichkeit von Strukturen in galaktischem Ausmaß geht. Auch Spock fände das faszinierend. Vielleicht auch eure Schüler - zumal das über mathematische Formeln nachgewiesen wurde.
Freie Programme
❱22Q4❱ ➜ de-wikipedia-org-wiki-MandelbulberSpezialisiert ist das Programm auf dreidimensionale Fraktale wie Mandelbulb, Mandelbox oder IFS, jedoch lassen sich auch Fraktale anderer Dimensionen visualisieren und rendern. M
Wikipedia
❱22Q4❱ ➜ de-wikipedia-org-wiki-Iteriertes-FunktionensystemIterierendes Funktionensystem
❱22Q4❱ ➜ de-wikipedia-org-wiki-Kategorie: Fraktale-Geometrie
Kategorie Fraktale Geometrie
❱22Q4❱ ➜ de-wikipedia-org-wiki-Julia-Menge
Julia-Menge
❱22Q4❱ ➜ de-wikipedia-org-wiki-Fraktalgenerator
Wikipedia-Eintrag: "Fraktalgenerator"
❱22Q4❱ ➜ de-wikipedia.org-wiki-Lindenmayer-System
Lindenmayer-System - ein Formelsystem, das den Getreiden ähnliche Strukturen erzeugt
❱22Q4❱ ➜ de-wikipedia.org-wiki-Mandelbrot-Menge
Mandelbrot-Menge
Magische Quadrate, Sechsecke, Kreise, Würfel etc.
➜ Abschnitt ansehen / wegblenden
Mathematische Grundlagen
Im magischen Quadrat sind natürliche Zahlen in einem Quadrat so angeordnet, dass die Summe der Zahlen in jeder Zeile, in jeder Spalte und in jeder Diagonale gleich ist. Diese Summe wird "magische Zahl" des Quadrats genannt und ergibt sich aus dieser Formel:
In einem Quadrat der Kantenlänge n müssen die Zahlen von 1 bis n2 so eingetragen werden, dass die Summe jeder Zeile, Spalte und Diagonale Sn ergibt. Das einfachste magische Quadrat hat die Kantenlänge 3 und 9 Felder - es ist das magische Quadrat aus Goethes Hexeneinmaleins - mit der "magischen Zahl" 15:
Sn = (33+3)/2 = (27+3)/2 = 30/2 = 15
Die ersten "magischen Zahlen" ab n = 0 aus dieser Formel sind: 0, 1, 5, 15, 34, 65, 111, 175, 260, 369, 505, …
Dabei ergeben die ersten drei Ergebnisse der Reihe jedoch keine magischen Quadrate.
Goethes Hexeneinmaleins
Das "Hexeneinmaleins" aus Goethes "Faust"ist die Bauanleitung für ein "Normales Magisches Quadrat"
Du mußt verstehn!
Aus Eins mach' Zehn,
Und Zwei laß gehn,
Und Drei mach' gleich,
So bist Du reich.
Verlier' die Vier!
Aus Fünf und Sechs,
So sagt die Hex',
Mach' Sieben und Acht,
So ist's vollbracht:
Und Neun ist Eins,
Und Zehn ist keins.
Das ist das Hexen-Einmal-Eins!
❱21❱ ➜ spektrum-de-wie-man-aus-hexenreimen-ein-magisches-quadrat-konstruiert
Hier wird der Bauplan erklärt, wie aus dem Hexeneinmaleins das magische Quadrat konstruiert wird.
Die ersten beiden Zeilen geben an, dass einem Kästchen neun weitere hinzugefügt werden. Damit entsteht ein 3-er Quadrat - denn in der letzten Zeile steht, dass das zehnte Kästchen entfällt.
"Zwei lass gehen" bedeutet, dass die 2 auf die dritte Position wandert.
"Die Drei mach gleich" wandert also ebenfalls und steht nun im Kästchen hinter der 2.
"Verlier' die Vier" - man lässt sie weg.
"Aus Fünf und Sechs - So sagt die Hex', Mach' Sieben und Acht" - wo nun 5 und 6 stehen sollten, werden 7 und 8 geschrieben. Damit ist der Grundaufbau erledigt.


Nun muss nur noch jeweils zur Quersumme 15 ergänzt werden. Quersumme von 15 ist 6. Und somit ergibt sich in jede Richtung "The number of the beast" - die Hexen- oder Teufelszahl ;-)
Mehr zur "Zahl des Teufels, der "Number of the beast" findet ihr weiter oben bei den Magischen Zahlen unter "Zahlenmystik"
Dieses Quadrat ist das einzige "Normale Magische Quadrat" der Größe 3 mal 3 und war bereits aus China ca. 2800 v. Chr. als "Lo-Shu" bekannt (Quelle: Wikipedia "Magisches Quadrat")
Bei einem "Normalen Magischen Quadrat" ergeben auch die Diagonalen die selbe Quersumme, wie die Senkrechten und Waagrechten.
❱24Q4❱ ➜ is-ecom-090_philo
Das Hexeneinmaleins als Multiplikationsaufgabe
❱21❱ ➜ trixonline-ch-Seiten-HexenEinMalEins
Noch eine Darstellung zur Herleitung des Hexen-Quadrates
❱21❱ ➜ de-wikipedia-org-Hexeneinmaleins
Artikel der Wikipedia zum Hexeneinmaleins, in dem eine weitere Interpretation gezeigt wird.
❱24Q4❱ ➜ zum-de-Faecher-gym-faust-hexen-einmaleins_2
Das Hexen-Einmaleins - mit Bezug zum Dualsystem und Leibnitz
❱24Q4❱ ➜ zum-de-Faecher-gym-faust-hexen-einmaleins_3
Das Hexen-Einmaleins - als "Wegbeschreibung" durch den jüd. Lebensbaum der Kabbala
❱24Q4❱ ➜ zum-de-Faecher-faust-einseins
Detaillierte Darstellung der Herleitung des Hexeneinmaleins
❱24Q4❱ ➜ zum-de-Faecher-gym-faust-hexen-wfleischer_09
Umdeutung der 10 gebote durch das Hexen-Einmaleins
Linktipps zu Zauberquadraten / Magischen Quadraten
❱21❱ ➜ anthrowiki-at-Magisches_QuadratAnthroposophen befassen sich gerne mit mystischen Zeichen und seltsamen Gedanken - so ist es auch nicht verwunderlich, dass den magischen Quadraten im Anthro-Wiki breiter Raum eingeräumt wird. Sei's drum. Mathematik ist nicht mystisch. Nur manchmal mysterisch.
❱21❱ ➜ artype.de-dossier.pdf
Ein Artikel aus "Spektrum der Wissenschaft" zu lateinischen magischen Quadraten, bei denen es um Farbanordnung geht, griechisch-lateinische Quadrate, sowie Magische Quadrate ungerader Ordnung
❱21❱ ➜ doermann-com-square
Online-Generator für "Perfekte magische Quadrate"
❱21❱ ➜ hp-gramatke-de-magic_sq-german-page0020
Umfangreiche Seite zu Magischen Quadraten: "Magische Quadrate sind keine Erfindung neuzeitlicher Algebraiker und Zahlentheoretiker. Zahlenschemata, die besondere Eigenschaften aufweisen, sind schon lange bekannt. Die überraschenden arithmetischen Eigenschaften der magischen Quadrate ließen frühere Kulturen auf besondere magische Kräfte schließen. Hier begegneten sich Kult und Numerologie."
❱21❱ ➜ hp-gramatke-magic_sq-page0090.htm
Eulersche Quadrate
❱21❱ ➜ mathematische-basteleien.de/magquadrat.htm
Magische Quadrate - hier wird auch das "antimagische Quadrat" erwähnt, bei dem alle Summen unterschiedlich sind, ebenso der Magische Würfel, die Magische Pythagoras-Figur, Magische Sechsecke, der Magische siebeneckige Stern, sowie der magische Kreis
❱21❱ ➜ math.uni-bielefeld-PUZZLES-magic-hexagon
Magische Sechsecke - Beispiele von der Uni Bielefeld
❱21❱ ➜ num-math-uni-goettingen-werner-schmankerl
Hier sind auf Seite 265 mathematische Erklärungen und mathematische Lösungsstrukturen zur Erstellung von magischen Quadraten zu finden
Wikipedia
❱21❱ ➜ Wikipedia: Lateinisches Quadrat (Farbmuster)❱21❱ ➜ Wikipedia: Magischer Würfel
❱21❱ ➜ Wikipedia: Magisches Klangquadrat
❱21❱ ➜ Wikipedia: Magisches Sechseck
❱21❱ ➜ Wikipedia: Magisches Quadrat
❱21❱ ➜ Wikipedia: Sator-Quadrat
❱21❱ ➜ Wikipedia: Vollkommen perfektes magisches Quadrat
Linksammlungen zum Hexeneinmaleins
❱21❱ ➜ hp-gramatke-page9100Linkliste
❱21❱ ➜ mathematische-basteleien-Magische%20Quadrate%20im%20Internet
Linkliste
Literatur
❱24Q3🛒 [Affiliate-Link] ➜ Zahlen, Spiralen und magische QuadrateLängen und Wellenlänge
Wie lang ist ein Muggaseggele?➜ Abschnitt ansehen / wegblenden
- Am deutlichsten (und experimentell in der Grundschule am leichtesten nachvollziehbaren Methode) wird die Notwendigkeit einer gemeinsam als Standard festgelegten Maßeinheit durch die Maßeinheit "Fuß".
Auf den ersten Blick vermuten die Kinder, dass ihre Füße gleich groß sind. Wenn sie dann (wie beim Zusammenstellen der Fußballmannschaft) Fuß an Fuß durch das Klassenzimmer gehen und zählen, wie oft sie ihre Füße hintereinander stellen könne, wird klar, dass verschiedene Ergebnisse entstehen. Durch die Bankreihe kann man zwei oder vier Schüler die Länge des Klassenzimmers messen und die Ergebnisse vergleichen lassen. - Was ist überhaupt 1 Meter?
- Per Definition sollte der Meter den 10-millionsten Teil des Erdquadranten auf dem Meridian von Paris betragen - also den zehnmillionsten Teil der Entfernung vom Nordpol über Paris zum Äquator.
- Da dies - wie sich herausstellte - immer noch zu ungenau war, wurde 1960 folgende Definition festgelegt:
- Ein Meter ist das 1 650 763,73-fache der Wellenlänge der von Atomen des Nuklids 86Kr beim Übergang vom Zustand 5d5 zum Zustand 2p10 ausgesandten, sich im Vakuum ausbreitenden Strahlung. siehe Wikipedia: Meter
Alles klar?
Dann is ja jut. - Die kleinste schwäbische Längeneinheit ist das "Muggasäggele".
Der Begriff stammt ursprünglich von der Schwäbischen Alb. Dort war die Schafzucht weit verbreitet und als "Säckel" wurden die Hoden eines Schafsbockes bezeichnet. Das "Muggasäckele" hat daher seinen Ursprung in der Längenbezeichnung des Hodensackes einer männlichen Stechmücke. Da Mücken etwas kleiner als Fliegen sind, gilt das "Muggaseggele" als Maßeinheit schwäbischer Genauigkeit und Präzision. Zur genaueren Bestimmung dieser Größeneinheit kann man vereinfacht folgende proportionale Beziehung aufstellen:
- Ein Mensch mit einer Körpergröße von 180 cm besitzt im Durchschnitt einen 4 cm langen Hoden.
- Die Hodenlänge einer 8 mm langen Stechmücke beträgt grob geschätzt und proportional gerechnet 0,177 mm
- Ein "Schwäbisches Präzisions-Muggasäggele" bezeichnet somit eine Länge von ca. 180 µm - Das nächst gelegene Dorf ist etwa 10 km entfernt. Diese Strecke legt ein geübter Wanderer in weniger als einer Stunde zurück.
- Klappt man dieselbe Strecke senkrecht nach oben, erreicht man bereits die untere Schicht der Stratosphäre, in der kein Mensch mehr Überleben kann, weil zu wenig Sauerstoff vorhanden ist.
- Setzt man diese Strecke in Relation zum Radius der Erde (6000 km), so entsprechen diese 10 km einem sechshundertstel des Erdradius.
- Beim tiefsten Loch, das die Menschen bisher gebohrt haben (im russischen Murmansk) erreichten sie eine Tiefe von knapp über 12 Kilometern.
- Bei einem Erdmodell-Luftballon mit 1,20 m Durchmesser müsste die atembare Luftschicht proportional mit einer Höhe von 1 mm dargestellt werden.
- Und - man merke auf! - die Humusschicht von 30 cm Dicke, von der wir unsere Nahrung beziehen, wäre nicht mehr als ein Hauch... - Ein Atom besteht zu 99,9% aus leerem Raum. Somit besteht auch ein Mensch nur zu 0,1% aus real greifbarer Materie.
Stellt man den Atomkern in der Größenrelation als Stubenfliege (siehe Muggasäggele) dar, die sich im Zentrum des Kölner Doms befindet, haben die Elektronen ungefähr einen Abstand zum Kern wie die Wände des Doms. Der Rest ist leerer Raum.
Wir können uns nur sehen, weil unsere Augen auf das Spektrum der Wellenlängen zwischen 400 nm und 700 nm "geeicht" sind. Diese Wellenlängen sind größer als der Durchmnesser eines Atoms und werden daher reflektiert. Nur deshalb können wir uns und den Rest der Materie sehen.
Wären unsere Augen auf den Bereich von 10-3 nm geeicht, würden wir durch uns "hindurchsehen" - und hätten den "Röntgenblick". siehe auch ➜ hhu-de-biodidaktik-Fotosynthese_neu-dateien-licht-licht"
Schon klar, liebe Atomphysiker - diese Vorstellung ist natürlich Quatsch und entspringt einem Modell des Atomaufbaues aus dem 19.Jahrhundert... Ist jedoch trotzdem faszinierend.
Selbstverfreilich surren die Leptonen, Bosonen (z.B. Photonen), Quarks usw. in diesem "luftleeren Raum" kreuz und quer durcheinander und füllen ihn somit aus. Ausserdem befindet sich 99 % der sichtbaren Materie im Universum im Plasmazustand.
Aber sei's drum. Ich bin unsichtbar! Zumindest für alle, die im kurzwelligeren Bereich sehen.
Wissenschaftlich genutzte
Wie war das nochmal mit dem Femtometer?➜ Abschnitt ansehen / wegblenden
| Bezeichnung | Symbol | Faktor | Vielfaches | Anmerkungen für Beispiele solcher Längen siehe Größenordnung (Länge) |
|---|---|---|---|---|
| Myriameter | 104 | 10 km | veraltet, siehe Myriameterstein, nicht SI-konform | |
| Kilometer | km | 103 | 1 000 m | |
| Hektometer | hm | 102 | 100 m | vor allem verwendet bei Artillerie und Marine, Hektometerstein an Straßen |
| Dekameter | dam | 101 | 10 m | zunächst offiziell Kette[6] |
| Meter | m | 100 | 10 dm | zunächst offiziell Stab[6] |
| Dezimeter | dm | 10-1 | 10 cm | veraltet Decimeter (um 1900) |
| Zentimeter | cm | 10-2 | 10 mm | zunächst Neuzoll[6] |
| Millimeter | mm | 10-3 | 1 000 µm | zunächst Strich[6] |
| Mikrometer | µm | 10-6 | 1 000 nm | veraltet Mikron, im technischen Sprachgebrauch auch kurz µ (Aussprache "mü") |
| Nanometer | nm | 10-9 | ||
| Ångström | Å | 10-10 | 100 pm | früher gebräuchlich für optische Wellenlängen und in der Kristallographie |
| Pikometer | pm | 10-12 | 1 000 fm | |
| Femtometer | fm | 10-15 | in der Kern- und Teilchenphysik als Fermi | |
| Attometer | am | 10-18 | ||
| Zeptometer | zm | 10-21 | ||
| Yoctometer | ym | 10-24 | ||
| Rontometer | rm | 10-27 |
Internationale Längeneinheiten
➜ Abschnitt ansehen / wegblenden
| Meter ausgedrückt in Nicht-SI-Einheiten | Nicht-SI-Einheiten ausgedrückt in Meter |
|---|---|
| 1 Meter ˜ 3,2808 Fuß | 1 Fuß ˜ 0,3048 Meter |
| 1 Meter ˜ 0,00062 Meilen (International) | 1 Meile (International) ˜ 1609,344 Meter |
| 1 Meter ˜ 0,00062 Meilen (US survey mile) | 1 Meile (US survey mile) ˜ 1609,3472 Meter |
| 1 Meter ˜ 0,00054 Seemeilen | 1 Seemeile = 1852,0 Meter |
| 1 Meter ˜ 1,0936 Yard | 1 Yard ˜ 0,9144 Meter |
| 1 Meter ˜ 39,370 Zoll | 1 Zoll ˜ 0,0254 Meter |
Quellenangabe: Tabellen aus Wikipedia:Meter
❱21❱ ➜ de-wikipedia-org-Längenmaß
Längenmaße verschiedener Nationen werden hier der Größe nach aufgelistet
Volumenberechnungen
➜ Abschnitt ansehen / wegblenden
Leicht makaber - aber mathematisch interessant: Wie viele Menschen passen in den Bodensee?
- Annahme 1: Im Mittelwert (von Baby bis Greis) wiegt ein Mensch 50 kg
- Annahme 2: Ein Mensch besteht zu 60-90% aus Wasser. Knochen sind leichter, das Hirn oft vernachlässigbar, Leber und Darm schwerer. Rechnen wir also mit dem spezifischen Gewicht von Wasser: 1 kg = 1 Liter
- Annahme 3: Somit hat ein Mensch im Welt-Durchschnitt ein Volumen von 50 Litern
- Derzeit leben knapp 8 Mrd Menschen auf der Erde. Diese haben somit ein Gesamtvolumen von 400 Mrd Litern, bzw. 400 Mio Kubikmetern.
- Der Bodensee hat ein Volumen von 48 Kubikkilometern. Das sind 48 Milliarden Kubikmeter, bzw. 48 Billionen Liter
- Wir rechnen mit Zehnerpotenzen:
- Rechenweg 1: Wie oft passen 400 Mio Kubikmeter in 48 Milliarden Kubikmeter?
- 48x109 / 400 x 106 = 48x109 / 4 x 108 = 480 / 4 = 120
- Rechenweg 2: Wie oft passen 50 Liter in 48 Billionen Liter?
- 48x1012 / (8x109x50) = 48x1012 / (400x109) = 48x1012 / (4x1011) = 480/4 = 120 (Ein Hoch auf das Rechnen mit Zehnerpotenzen!)
- Die gesamte Menschheit könnte somit (in flüssigem Zustand und im mathematischen Denkmodell) annähernd 120 mal im Bodensee versenkt werden.
Die Rechnung taucht weiter unten bei den Fermi-Aufgaben nochmal auf: Menschen im Bodensee - dort habe ich weitere Rechnungen dazu abgelegt.
Variante: Wenn die Menschheit eingeäschert würde - welches Volumen bliebe übrig?
- Annahme 1: Im Mittelwert (von Baby bis Greis) wiegt ein Mensch 50 kg
- Annahme 2: Ein Mensch besteht zu 60-90% aus Wasser. Rechnen wir also mit 25% "Trockenmasse"
- Annahme 3: Somit hat ein Mensch im Welt-Durchschnitt ein Trockengewicht von 12,5 kg, bzw. ein "entwässertes Volumen von 12,5 Litern
- Derzeit leben knapp 8 Mrd Menschen auf der Erde. Diese haben somit ein Gesamtvolumen von 12,5 * 109 Litern.
- Das entspricht ca. einem Würfel mit 12,5 * 106 m3
- Die Kaaba in Mekka ist 13,10 m hoch und hat eine Grundfläche von 11,03 m × 12,62 m, besitzt also ~ ein Volumen von ~ 1800 m3
- Die Menschheit könnte somit in knapp 7000 Urnen mit der Größe der Kaaba abgefüllt werden.
Gewicht der Luft im Klassenzimmer
Die Luft in einem durchschnittlichen, völlig leeren Klassenzimmer (h=3m, b=6,50m, l=10m) wiegt - bei einem spezifischen Gewicht von 1,3 g/Liter Luft etwa eine viertel TonneHistorische Gewichtsmaße
Wie viel Quentchen hat ein Skrupel?➜ Abschnitt ansehen / wegblenden
siehe auch ➜ wikipedia:Alte_Maße_und_Gewichte_(deutschsprachiger_Raum)
Anmerkung: Hier sieht man, weshalb noch heute in Bayern auf dem Oktoberfest weniger Bier im Glas ist ;-)
Aktuelle und historische Gewichtseinheiten im Anglo-Amerikanischen System
| Maßeinheit | entspricht | In Gramm | |
|---|---|---|---|
| 1 Pfund | =12 Unzen | 345,6 g | |
| 1 Unze | =8 Drachmen | 28,8 g | Onza=30g |
| 1 Drachme | =3 Skrupel | 3,6 g | Drachme= Silbermünze |
| 1 Skrupel | =20 Gran | 1,2 g (1,25 g) | Skrupulus= Steinchen |
| 1 Gran | 0,06 g | Granum= Getreidekorn | |
| 1 Loth | 1/32 Pfund | ||
| später 1/30 Pfund | 13,6 g | ||
| 1 Quint | ¼ Lot | 3,65 g | |
| später 1,67 g | „ein Quentchen“ | ||
| Maaß: | Regional verschiedene Hohlmaße | ||
| Baden/ Schweiz | 1,5 l | ||
| Bayern | 1,06 l | ||
| Frankfurt a.M. | 1,793 l | Alt: 1,599 l | |
| Württemberg | Iralleichmaß | 1,837 l | |
| Duteich-Maß | 1,917 l | ||
| Schenk-Maß | 1,67 l | ||
| Österreich | 1,415 l | ||
| Hessen | 1,95 l | bzw. 2 l |
Angloamerikanische Gewichtseinheiten
❱21❱ ➜ de-wikipedia-org-Angloamerikanisches_Maßsystem-GewichtseinheitenAktuelle und historische Gewichtseinheiten im Anglo-Amerikanischen System
Zeitmessung Zeitdarstellung
Zeitleisten und Zeitschienen - Wie kann man Zeitdimensionen anschaulich darstellen?Wie zeigt man 4 Milliarden Jahre der Erdgeschichte? Und wie viel bleibt für uns?
➜ Abschnitt ansehen / wegblenden
➜ siehe auch
Urzeit und Dinosaurier
➜ siehe auch Zeitleisten / Zeitstrahlen
➜ siehe auch Sonnenuhren bauen
➜ siehe auch Tabelle kalender5.xls
Dieses Arbeitsblatt enthält eine Tabelle zur Berechnung des Lebensalters in Tagen, Minuten und Sekunden, sowie einen auf dem Geburtstag per Zufallsfunktion erzeugten Biorhythmus, ein Chinesisches Horoskop und einen ewigen Kalender. Ergänzt habe ich 2017 einen immerwährenden Dodekaederkalender zum Ausschneiden und Zusammenbastelnbasteln. Größenanpassung erfolgt durch prozentuale Angabe beim Ausdrucken.
➜ siehe auch Zeitleisten / Zeitstrahlen
➜ siehe auch Sonnenuhren bauen
➜ siehe auch Tabelle kalender5.xls
Dieses Arbeitsblatt enthält eine Tabelle zur Berechnung des Lebensalters in Tagen, Minuten und Sekunden, sowie einen auf dem Geburtstag per Zufallsfunktion erzeugten Biorhythmus, ein Chinesisches Horoskop und einen ewigen Kalender. Ergänzt habe ich 2017 einen immerwährenden Dodekaederkalender zum Ausschneiden und Zusammenbastelnbasteln. Größenanpassung erfolgt durch prozentuale Angabe beim Ausdrucken.
Zeitschiene 1
Zur Illustration der Erdzeitalter sind diese Karten der Plattentektonik und der Kontinentalverschiebung gut geeignet:❱21❱ scotese.com/earth
- 400 Meter → 4 Mrd Jahre: Urknall - Entstehung der Erde, Glutball & Abkühlungsphase = Hälfte der bislang vergangenen Zeit
- 200 Meter → 2 Mrd Jahre → Bildung der Urkontinente und Urmeere, erste Algen (Algonikum) und Urzeller
- 90 Meter → 900 Mio Jahre → tierische Lebewesen, die Sauerstoff atmen
- 40 Meter → 400 Mio Jahre → Pangäa, erste Landpflanzen, erste Landtiere
- 20 Meter → 200 Mio Jahre → Beginn des Trias, erste Säugetiere
- 6,5 Meter → 65 Mio Jahre → Ende der Kreidezeit, Beginn der Erdneuzeit, Ende der Dinosaurier
- 4 Meter → 40 Mio Jahre → Affen und erste Menschenaffen
- 2 Meter → 20 Mio Jahre → Proconsul ( Uraffe)
- 80 Zentimeter → 8 Mio Jahre → erste Urmenschen
- 20 Zentimeter → 2 Mio Jahre → Australopiticus, erster "homo" und homo habilis, homo erectus
- 10 Zentimeter → 1 Mio Jahre →
- 2,5 Zentimeter → 250.000 Jahre → homo sapiens
- 1,5 Zentimeter → 150.000 Jahre → homo sapiens sapiens
- 1 mm→ 10000 Jahre → Nacheiszeit, Beginn der Jungsteinzeit, der Mensch wird sesshaft
- 0,2 mm → Jesu Geburt
- 0,0001 mm → Das vergangene Jahr
Zeitschiene 2
- 201 Meter stellen 2010 Jahre seit Christus dar
- 0 Meter → 2010 Jahre → Jahr 0 → Christus Geburt
- 50 Meter → Jahr 500 → Ende des römischen Reiches
- 75 Meter →Jahr 750 → Karl der Große
- 150 Meter → Jahr 1500 → Entdeckung Amerikas
- 180 Meter → Jahr 1800 → Französische Revolution / Napoleon
- 190 Meter → Jahr 1900 = erstes Auto
- 195 Meter = Jahr 1950
- 199 Meter = Jahr 1989 = Wiedervereinigung
- 200 Meter = Millennium
- 200 Meter bis 201 Meter = Lebenszeit eines heute zehn Jahre alten Kindes
Zeitschiene 3
▶ Man kann das auch mit einer Rolle Klopapier machen. Die hat 200 Blatt, würde dann der oben angegebenen Abfolge entsprechen, braucht aber nur ca. 25 Meter, bei 12,5 cm pro Blatt. Der Umfang eines Standardklassenzimmers beträgt 36 m. Passt also gut einmal rum rein.Geschwindigkeit
Wie schnell sind wir eigentlich?➜ Abschnitt ansehen / wegblenden
- Die Erde rotiert am Äquator
Der zurückgelegte Weg ist der Erdumfang s = 2 * Pi * r, wobei r = 6378 km den (gerundeten) Erdradius darstellt.
Der Erdumfang am Äquator beträgt somit s = 40.074 km.
Die dafür benötigte Zeit beträgt 1 Tag = 24 Stunden
Die Rotationsgeschwindigkeit der Erde somit v = s/t = 40.074 km/24 h = 1670 km/h
Das ist Überschall-Geschwindigkeit - am Äquator.
Wir befinden uns jedoch nicht am Äquator. Ich lebe in der Nähe vom Bodensee, etwa am 48sten Breitengrad. Nach dem Rechenbeispiel oben bei "Kreisumfang" beträgt der Umfang der Erde - wenn ich mich auf diesem Breitengrad bewege - 26.700 km. Hier bin ich "nur noch" mit 1112 km/h unterwegs.
Nebenbei: Würde die Erde aufhören, sich zu drehen, die Atmosphäre sich jedoch (wegen der Trägkeit der Masse) mit der normalen Geschwindigkeit weiter drehen, gäbe es Stürme von bislang unbekannten Ausmaßen mit Windgeschwindigkeiten über 1000 km/h, die jedes Gebäude, alle Pflanzen und Tiere zerstören würden. Die einzigen Überlebenden wären die Bewohner der Forschungsstation in der Antarktis, weil die Geschwindigkeit der sich bewegenden Atmosphäre in Bezug zur Erdoberfläche zu den Polkappen hin abnähme - Die Erde bewegt sich um die Sonne. Die mittlere Bahngeschwindigkeit der Erde beim Umlauf um die Sonne berägt 29,78 km/s.
Das sind ca. 107.000 km pro Stunde,
Jeder von uns ist im Augenblick mit mehr als 100.000 Stundenkilometern unterwegs - im Bezug zur Sonne - ❱21❱
siehe auch ➜ astrokramkiste-planeten-tabelle
Umlaufzeiten und Entfernungen der Planeten
Prozentrechnen
Erhabene Zahlen, vollkommene Zahlen, glückliche Zahlen➜ Abschnitt ansehen / wegblenden
Klimadiskussion
In der laufenden Klimadiskussion liest man immer wieder folgende Argumentation:"Der Anteil des CO2 an der Atmosphäre beträgt 0,04%
"Der Anteil des natürlichen CO2 an der Atmosphäre beträgt 0,0384%
"Der Anteil des menschengemachten CO2 an der Atmosphäre beträgt 0,0016%
Soooo wenig kann doch gar nicht schädlich sein."
Schaun' mer mal:
Bei einem erwachsenen Menschen mit ca. 80 kg beträgt die tödliche Dosis etwa 230 mg Cyanid. Das sind 0,0002875 %.
Bei 0,0001 % wird dir nur schlecht - das aber heftig. Bei 0,00016 % brauchst du vermutlich den Notarzt. So wie im Augenblick unsere Erde.
Wenig kann ganz heftig weh tun und zerstören.
Durchschnitt + Mittelwert
➜ Abschnitt ansehen / wegblenden
Bei Klassenarbeiten gebe ich nie den Notendurchschnitt der Klasse an. Weshalb? Weil diese Angabe sinnlos ist. Der Notendurchschnitt sagt nichts über die Leistung der Schüler dieser Klasse aus. Bei einem Notenschnitt von 3,0 können neun Schüler eine 1, neun Schüler eine 5 und zwei Schüler eine Drei erreicht haben. Oder 20 Schüler eine 3. Oder fünfzehn Schüler eine 2 und fünf Schüler die 6 (weil sie abgeschrieben haben und erwischt wurden).
Welche Klasse ist besser? Welcher Lehrer hat besser unterrichtet?
Kokolores.
Der Notendurchschnitt macht nur als Berechnung der Individualleistung eines Schülers Sinn.
Nun steigt der reichste Mensch Deutschlands ein (Aldi-Besitzer Karl Albrecht, geschätztes Vermögen 25 Mrd. €)
Wie ändert sich das Durchschnittsvermögen im Bus, wenn der Durchschnitt zuvor bei 54.000 € lag?
Da hätte jeder im Bus plötzlich eine halbe Milliarde. Im Schnitt.
(nach Rolf Dobelli, Die Kunst des klugen Handelns, München, DTV, 2014, S. 17)
Diese Zahlen sagen nichts aus. Sie taugen nicht dazu, valide Feststellungen zu treffen. Durchschnitte machen nur dort Sinn, wo es keine Extremwerte gibt.
BTW: Zum Durchschnittsvermögen: In Deutschland besaßen 2009 die reichsten 5 % der Bevölkerung 46 % des privaten Gesamtvermögens, das reichste Prozent besaß 23 %, wobei die reichsten 100 Familien vermutlich nicht in der Statistik enthalten sind. (Quelle:de-wikipedia-org-wiki-Vermögensverteilung_in_Deutschland)
Welche Klasse ist besser? Welcher Lehrer hat besser unterrichtet?
Kokolores.
Der Notendurchschnitt macht nur als Berechnung der Individualleistung eines Schülers Sinn.
... im Schnitt
... ist ein Fluss nur 1 m tief. Wer nach dieser Aussage als Nichtschwimmer den Fluss frohen Mutes durchschreiten will, wird sterben. Denn in der Mitte kann es sich trotzdem um einen 10 Meter tiefen, reißenden Strom handeln.Das Busbeispiel
Ein Bus ist mit 49 Menschen besetzt. Nun steigt der schwerste Mensch Deutschlands zu. Wie ändert sich das Durchschnittsgewicht der Menschen im Bus? Wenige Prozent.Nun steigt der reichste Mensch Deutschlands ein (Aldi-Besitzer Karl Albrecht, geschätztes Vermögen 25 Mrd. €)
Wie ändert sich das Durchschnittsvermögen im Bus, wenn der Durchschnitt zuvor bei 54.000 € lag?
Da hätte jeder im Bus plötzlich eine halbe Milliarde. Im Schnitt.
(nach Rolf Dobelli, Die Kunst des klugen Handelns, München, DTV, 2014, S. 17)
Sinnlose Schnitte
- Was ist die durchschnittliche Größe einer Stadt?
- Was ist die durchschnittliche Tiefe der Meere?
- Wieviele Tote fordert ein Krieg im Durchschnitt?
- Wie hoch fliegen Flugzeuge im Durchschnitt?
- Wieviel kostet ein Kunstwerk im Durchschnitt?
- Wieviel verdient ein Unternehmer im Durchschnitt?
- Welches Vermögen haben die Deutschen im Schnitt?
Diese Zahlen sagen nichts aus. Sie taugen nicht dazu, valide Feststellungen zu treffen. Durchschnitte machen nur dort Sinn, wo es keine Extremwerte gibt.
BTW: Zum Durchschnittsvermögen: In Deutschland besaßen 2009 die reichsten 5 % der Bevölkerung 46 % des privaten Gesamtvermögens, das reichste Prozent besaß 23 %, wobei die reichsten 100 Familien vermutlich nicht in der Statistik enthalten sind. (Quelle:de-wikipedia-org-wiki-Vermögensverteilung_in_Deutschland)
Wahrscheinlichkeit, Lotto, Gewinne
➜ Abschnitt ansehen / wegblenden
Lotto
Wie hoch ist die Wahrscheinlichkeit 6 Richtige beim Lotto (6 aus 49) zu haben?Wie viele unterschiedliche Lottokästchen müsste man ausfüllen, um einen Sechser zu bekommen?
Berechnung
(49*48*47*46*45*44) / 6! (geteilt durch 6 Fakultät)
denn nach jeder gezogenen Kugel ist eine weniger im Spiel
bzw: (49*48*47*46*45*44) / 6*5*4*3*2*1 = 10.068.347.520 / 720 = 13.983.816
Die Wahrscheinlichkeit liegt somit bei ca. 1:14 Millionen
Ein "Dreier" ist leichter zu bekommen
(49*48*47) / 3! (geteilt durch 3 Fakultät)
bzw: (49*48*47) / 3*2*1
Für den Jackpot multipliziert sich das Ergebnis mal 10 für die Superzahl - damit liegt die Wahrscheinlichkeit bei 1:140 Millionen.
Veranschaulichung der Gewinnchance im Lotto
Der Durchmesser eines Tischtennisballs (was etwa dem Durchmesser der Ziehungskugel entspricht) beträgt 40 mm. Wenn wir errechnen wollen, welche Maße ein Raum haben muss, in den 140 Millionen Tischtennisbälle passen, nehme ich der Einfachheit halber den Mittelwert zwischen dem Kugelvolumen und dem Würfelvolumen als Näherungswert - sonst wird's mathematisch ;-).Bei einem Durchmesser von 4 cm beträgt das Würfelvolumen 64 cm3
Das Kugelvolumen 33,51 cm3.
Mittelwert: ca. 49 cm3.
140 Millionen Tischtennisbälle benötigen somit ca. 140.000.000 * 49 cm3 = 140.000 * 49 dm2 = 140 * 49 m3 = 6860 m3
Als Würfel müsste der Kubus demnach eine Kantenlänge von 19 Metern aufweisen.
Oder man stellt 20 Würfel mit jeweils 7 Meter Kantenlänge nebeneinander, füllt diese mit weißen Tischtennisbällen und montiert bei jedem oben ein Sprungbrett.
In der ganzen Tischtennismenge befand sich ein einziger schwarzer Tischtennisball. Der Spieler sucht sich ein Sprungbrett, legt die undurchsichtige Tauscherbrille an, springt in einen der Würfel, taucht ab, wühlt sich durch, greift einen einzigen Tischtennisball.
Mit Glück den schwarzen.
Zur Debatte über Tempolimits auf Autobahnen
Tempo 130 - ja oder nein?Auf Autobahnen starben im Jahr 2019 "nur" 393 Menschen und auf Landstraßen dagegen 1552 Menschen. Zudem sind auf Autobahnen viel mehr Fahrzeuge unterwegs!
Also behaupten die Geschwindigkeitsbefürworter, die Autobahnen seien VIEL sicherer - man brauche kein Tempolimit!
Quelle: Statistisches Jahrbuch 2019, https://www.destatis.de/DE/Themen/Querschnitt/Jahrbuch/jb-transport-verkehr.pdf
Für den Zahlenvergleich habe ich die getöteten Fußgänger und Fahrradfahrer herausgerechnet, da diese auf Autobahnen in der Regel nicht auftauchen
Eigentlich müsste man auch die Unfallopfer herausrechnen, die durch Vorfahrtsverletzungen ums Leben kamen - denn es geht ja darum, die Gefahr durch die Geschwindigkeit zu beweisen - oder zu widerlegen.
WEIT GEFEHLT!
In Deutschland gibt es 13.000 km Autobahnen und 229.000 km Land-, Bundes- und Kreisstraßen (Quelle: a.a.O).
Setzt man die Zahlen ins Verhältnis, so kamen pro 1000 Straßenkilometer auf Autobahnen 30 Menschen ums Leben, auf den anderen außerörtlichen Straßen jedoch nur 7.
Verbildlicht:
Stellt man am Rand von Autobahnen für jeden Getöteten ein Kreuz auf, stehen nach 10 Jahren die Leichenkreuze (wenn man sie gleichmäßig verteilt) an Autobahnen in 3 Kilometer Abstand. Auf Landstraßen im Abstand von 14 Kilometern.
Die Wahrscheinlichkeit, auf einer Autobahn zu sterben ist mehr als vier Mal so hoch wie auf Landstraßen. Und da behaupten Leute ernsthaft, die Autobahnen seien sicher und man dürfe dort nach Belieben rasen. Die Gefahr geht besonders von der höheren Verkehrsdichte auf Autobahnen aus.
Durch die höheren Geschwindigkeiten ist auch die Impulsenergie höher. Zu betrachten wären somit auch die (volkswirtschaftlichen) Sachschäden auf Autobahnen im Vergleich zu den Sachschäden auf Land-, Kreis- und Bundesstraßen.
Würfelbilder
Gerhard Richter hat großformatige Bilder erstellt, die aus kleinen quadratischen Feldern bestehen. Die Farbverteilung wurde per Zufallsgenerator festgelegt. Im "Kleinen" können wir das mit Würfeln nachvollziehen. Im folgenden Beispiel habe ich mit der Tabellenkalkulation ein Raster erstellt, danach mit dem Würfel die Zahlen pro Feld erwürfelt und notiert. Jede Zahl erhielt dann eine eigene Farbe und wurde per Mausklick und Mehrfachauswahl durch *strg*-Taste eingefärbt. Im letzten Bild habe ich die Zahlen und Rahmen entfernt.Das Basis-Arbeitsblatt findet ihr hier als ➜ Excel-Blatt oder als ➜ PDF-Datei zum Download





Beim letzten Bild sieht man, dass die Zahlen jeweils fast in gleicher Anzahl gewürfelt wurden. Je mehr Flächen man verwendet, umso eher gleicht sich die Anzahl der Würfe an.
Im Kapitel zum "Goldenen Schnitt" habe ich ein Beispiel abgelegt, wie mit dieser Methode Flächen gleichwertig gefärbt werden können.
Spiralen, Schnecken, Kreissegmente
Vielecke und andere Konstruktionen➜ Abschnitt ansehen / wegblenden
❱21❱ ➜
archiv.schulkunst-bw-itemId=25765
Geometrische Konstruktionen 1887 - 1896 Zeichnungen H. und O. Schürger
❱21❱ ➜ antike-griechische.de/Euklid
Einführung in das Werk Euklids
❱21❱ ➜ kolibriethos.de/foto/index.php?twg_album= MathebuchDuerer&twg_offset=0
Das Mathematikbuch von A. Dürer aus dem Jahr 1525 für Künstler - Dürer verwendet den Tangens, das technische Zeichnen, kennt Netzpläne, Kegelschnitte, ... er widmet der Typographie ein eigenes Kapitel. Spannend sind auch die von ihm verwendeten Werkzeuge
❱21❱ ➜ archive-org-mathe.tu-freiberg.de/~hebisch/cafe/duerer/spiralen (längere Ladezeit, da aus archive-org eingebunden)
Die Schneckenlinien (Spiralen) bei A.Dürer













Geometrische Konstruktionen 1887 - 1896 Zeichnungen H. und O. Schürger
❱21❱ ➜ antike-griechische.de/Euklid
Einführung in das Werk Euklids
❱21❱ ➜ kolibriethos.de/foto/index.php?twg_album= MathebuchDuerer&twg_offset=0
Das Mathematikbuch von A. Dürer aus dem Jahr 1525 für Künstler - Dürer verwendet den Tangens, das technische Zeichnen, kennt Netzpläne, Kegelschnitte, ... er widmet der Typographie ein eigenes Kapitel. Spannend sind auch die von ihm verwendeten Werkzeuge
❱21❱ ➜ archive-org-mathe.tu-freiberg.de/~hebisch/cafe/duerer/spiralen (längere Ladezeit, da aus archive-org eingebunden)
Die Schneckenlinien (Spiralen) bei A.Dürer
Beispiele














Fermi-Aufgaben
➜ Abschnitt ansehen / wegblenden
Grundfragen / Ablauf zur Lösung von Fermi-Aufgaben
- Was musst du wissen, um die Aufgabe lösen zu können? Notiere die Fragen und Ideen! - Wo kannst du Informationen zu deinen Fragen bekommen? Eltern / Sekretariat / Hausmeister / Gemeinde / Internet / Bücherei ... - Versuche eine mathematische Lösung. Ist das Ergebniss sinnvoll? Kann das Ergebnis stimmen? Schätze. Diskutiere mit den Mitschülern / Gruppenmitgliedern. - Erstelle ein Plakat und präsentiere deine LösungZeit und Geschwindigkeit
- Wieviel Lebenszeit verbringt man mit Zahnpflege?
- Um wie viele Jahre wäre dein Leben kürzer, wenn du die Zeit, die du mit Handy, vor dem Fernseher und mit dem Computer verbringst, abziehst?
- Wie lange dauert es laut bis 1.000.000 zu zählen, wenn du jede Zahl aussprechen musst?
- Wie lange würdest du brauchen, um zu Fuß von Rügen nach Konstanz zu kommen?
- Wie lange würdest du brauchen, um zu Fuß auf dem ➜ Jakobsweg von Ulm nach Compostela zu kommen?
- Wie oft schließt der Lehrer im Schuljahr die Klassenzimmertür auf und zu?
- Wie viel würde es kosten, alle Schüler an jedem Schultag einen Monat lang mit 2 Kugeln Eis zu versorgen?
- Wie oft geht man im Schuljahr in die Pause?
- Wie viel Zeit verbringst du im Monat im Bad?
- Wie schnell ist der Osterhase?
- Wie viel Prozent der Zeit steht ein Auto ungenutzt herum?
- Wie viel (Lebens-)Zeit verbringt ein Schüler am Handy?
- Wie viel (Lebens-)Zeit haben wir verschwendet, indem wir auf die Uhr gesehen haben?
- Wie schnell ist der Weihnachtsmann? (siehe dazu auch: " ➜ Weshalb es den Weihnachtsmann nicht geben kann")
- Wenn du in den nächsten 60 Jahren jeden Tag genau so viel Zeit damit verbringst, etwas mit deinem Handy/Computer/Fernsehgerät zu tun wie gestern - wie viele Tage, Monate, Jahre werden das insgesamt gewesen sein?
Anzahlen / Mengen
- Aus wie vielen Atomen besteht deine Schule?
- Welches Wort sprichst du am häufigsten an einem Tag? Schreibe die 10 häufigsten Worte auf
- Wenn jeder Storch pro Tag 8 Häuser anfliegen kann - wie viele Störche müssen in Deutschland vorhanden sein, um die Geburtenrate gewährleisten zu können?
- Wenn man alle Zahlen zusammenzählt, die in einer Woche beim Lotto angekreuzt werden - wie groß wäre die Summe?
- Wie hoch wäre ein Turm aus dem Papier, das in deiner Schule jedes Jahr für Kopien verbraucht wird? Wie schwer ist dieser Turm? Könnte man mit dem Papier alle Klassenräume der Schule tapezieren?
- Wie lange könnte man eure Klasse mit den Bonbons vom Mainzer Karnevalsumzug versorgen?
- Wie oft blinzelt man am Tag?
- Wie oft dreht sich ein Autoreifen auf der Fahrt von Konstanz nach Lübeck?
- Wie oft sprichst du am Tag den Buchstaben "e"?
- Wie viel Kunststoffabfall entsteht täglich in Hotels und Ferienanlagen durch Margerine-, Marmelade- und Nutella-Plastik-Packungen weltweit?
- Wie viele Aufgaben muss ein Lehrer in seinem Leben korrigieren?
- Wie viele Bäume stehen in der Deutschen Aleenstraße?
- Wie viele Bananen isst du in deinem Leben?
- Wie viele Blätter sind an einem Baum?
- Wie viele Bleistifte Kreide, Toilettenpapier, wird jedes Jahr an eurer Schule verbraucht?
- Wie viele Bleistifte würdest du benötigen, um auf dem Äquator eine Linie um die Erde zu zeichnen?
- Wie viele Bratwürste werden in der Grillsaison verspeist?
- Wie viele Fahrzeuge stehen in einem 5km langen Stau?
- Wie viele Gottesdienste wurden wohl auf der ganzen Welt in den letzten zweitausend Jahren an Weihnachten gefeiert?
- Wie viele Grashalme wachsen auf einem Sportplatz?
- Wie viele Gummibärchen passen in eine Badewanne?
- Wie viele Gummibärchen passen auf einen Schultisch?
- Wie viele Haare hast du auf dem Kopf?
- Wie viele Hefte schreibt man während der Schulzeit voll?
- Wie viele Karokästchen kann ein Schüler in einer Schulstunde ausmalen, wenn er jedes zweite als Muster einzeln ausmalt?
- Wie viele Kaugummis kauen alle Schüler deiner Schule in einem Jahr? Wie viele Abfalleimer kann man damit füllen?
- Wie viele Klavierstimmer gibt es in Chicago? ( ➜ Fermis Ausgangsaufgabe)
- Wie viele Kleidungsstücke hast du in deinem Leben schon getragen? Wie viel haben sie alle zusammen gekostet? Wie lang wäre die Wäscheleine, auf der du alle aufhängen könntest?
- Wie viele Körperzellen enthält ein Mensch (ein Elefant)? (siehe oben)
- Wie viele Kreuze werden pro Woche beim Lotto gemacht? - Wie viele Mathehefte könnte man damit vollschreiben, wenn in jedes Kästchen ein Kreuz gemacht wird
- Wie viele LKW stehen auf der rechten Spur im 25-km-Stau zwischen Pforzheim und Karlsruhe?
- Wie viele Matheaufgaben stellt dein Lehrer in seinem Leben?
- Wie viele Mäuse passen in einen Elefanten?
- Wie viele Menschen passen in den Bodensee? (* siehe meine Rechnung dazu unten)
- Wie viele Musiknoten werden von einem Musiksender wie SWR3 im Jahr gespielt?
- Wie viele Nadeln hat ein Tannenbaum?
- Wie viele Nadeln hat ein Weihnachtsbaum?
- Wie viele Noten bekommst du in deiner Schulzeit?
- Wie viele Noten gibt ein Lehrer in seiner Laufbahn?
- Wie viele Noten hörst du, wenn du eine Stunde lang Musik hörst?
- Wie viele Papiertücher werden pro Woche an unserer Schule benutzt?
- Wie viele Pizzas werden in Baden-Württemberg pro Jahr gegessen?
- Wie viele Plastikdeckel haben die Plastikflaschen, die von den Schülern deiner Schule im Jahr getrunken werden?
- Wie viele Reiskörner isst ein Asiate in seinem Leben
- Wie viele Sandkörner sind in einem Sandkasten?
- Wie viele siehe auch ➜ Sattelschlepper-Modelle (1:87) passen in einen Sattelschlepper?
- Wie viele Sätze hast du in deinem Leben schon gesprochen?
- Wie viele Schneeflocken (einzelne Kristalle) benötigt man, um einen 150 cm grossen Schneemann zu bauen?
- Wie viele Schneeflocken fallen im Laufe eines Tages über einer mittelgroßen Stadt, wenn sie abends unter einer 10cm hohen Schneedecke liegt
- Wie viele Schüler benötigt man - wenn sie alle Hand in Hand stehen - um die Schule einzukreisen?
- Wie viele Schüler passen in den Klassenraum?
- Wie viele Schüler unterrichtet ein Lehrer bis zu seiner Pension?
- Wie viele Tintenpatronen ver"schreibt" ein Schüler in seiner Schulzeit?
- Wie viele Treppenstufen läuft man pro Schuljahr im Schulhaus?
- Wie viele Tüten Buchstabensuppe benötigt man, um daraus alle Seiten von "Harry Potter und der Stein der Weisen" (334 S.) zu legen?
Grundinformationen dazu: Der Buchstabe "e" ist mit 17,4% der häufigste Buchstabe. Eine Buch-Normseite hat 1000 Buchstaben. Eine 100g-Packung enthält etwa 800 Buchstaben. Vorsicht Falle: Nach Informationen der Hersteller sind in der Buchstabensuppe alle Buchstaben gleich häufig vertreten - Wie viele Verkehrsschilder stehen in deiner Stadt?
- Wie viele Regentropfen sind im Bodensee?
- Wie viele Zahlen hast du in deinem Leben schon geschrieben?
- Wie viele Zähne hat ein Zahnarzt im Laufe seines Lebens angebohrt? Wenn man alle Bohrungen zusammenrechnet - wie tief hat er gebohrt?
- Wie viele Zigaretten raucht ein Kettenraucher?
Prozent
- Wieviel Prozent der Bevölkerung sind Kinder
- Wie viel Prozent des Gebietes der Bundesrepublik werden von PKW abgedeckt?
- Wie viel Prozent des Gebietes eurer Stadt / Gemeinde werden von PKW abgedeckt?
- Wie viel Prozent des Gebietes der Bundesrepublik sind überdacht?
- Wie viel Prozent eines Arbeitsblatts sind schwarz bedruckt, wie viel Prozent weiß?
Volumina
Wasser / Flüssigkeit- Wenn ein Wasserhahn ein Jahr lang pro Sekunde 1x tropft - wie viele Tassen / Eimer / Badewannen / Tanklastzüge könnte man damit füllen?
- Wie viel Benzin/Diesel wirst du verbraucht haben, bis du deinen Führerschein machen kannst?
- Wie viel Benzin verbraucht ein Auto im Jahr? Wie viel trinkt ein Mensch im Vergleich? Was kostet mehr?
- Wie viel Benzin wird bei einem Stau von 10 km Länge verbraucht, wenn ein Fahrzeug den Stau nach 45 Minuten verlassen kann?
- Wie viel Ersatzkanister könnte man mit dem Verbrauch der Autos in Deutschland füllen?
- Wie viel Flüssigkeit trinkt die Klasse 4 pro Woche?
- Wie viele Kühe braucht man, damit alle Schüler der Schule täglich ein Glas Milch bekommen?
- Wie viel Liter Blut pumpt das Herz in einem ganzen Leben? (pro Takt etwa 100ml)
- Wie viel Wasser verbrauchst du in einer Woche?
- Wie viel Wasser, Klebstoff wird jedes Jahr an eurer Schule verbraucht?
- Wie viele Kühe braucht man, um die Schule eine Woche lang mit Milch zu versorgen?
- Wie viele Liter trinkst du im Jahr? Wie viele Badewannen könnte man damit füllen?
- Wie viele Liter Wasser wurden für die Herstellung aller Computer der Schüler deiner Schule benötigt? (Pro Computer ca. 20.000 Liter)
- Wie viele Liter Wasser wurden für die Herstellung aller Schulbücher deiner Schule benötigt?
- Wie viele Luftballons passen ins Klassenzimmer?
- Wie viele Schultaschen passen in ein Klassenzimmer?
- Wie viele Kühe werden benötigt um den Milchbedarf der Klasse/ der Schule/ der Stadt XY an einem Tag zu decken?
- Wie viele Stunden würde der Sauerstoff im Klassenzimmer für eure Klasse ausreichen, wenn keine Frischluftzufuhr erfolgt?
- Wie viele Luftballons passen in den Klassenraum?
- Beim Lotto 6 aus 49 steht die Wahrscheinlichkeit 1:139.868.160. Das bedeutet im Vergleich, dass unter knapp 140 Millionen weißen Tischtennisbällen einer schwarz angemalt wäre. Wie viel Platz brauchen 140 Millionen Tischtennisbälle?
- Wie viele Golfbälle passen in einen Koffer?
- Wäre die Kartoffel
➜ auf diesem Bild echt - wie viele Pommes könnte man daraus machen? Wenn man sie mit einem normalen Kartoffelschäler schälen würde - wie lang wäre die abgeschälte Schale? - Wie viel Kilogramm Hundekot werden in unserer Stadt an einem Tag 'produziert'? Wie viel in ganz Deutschland?
- Wie viel Gramm / Kilogramm Regenwurmkot entstehen in 100 m² Garten an einem Tag? Wie viel in ganz Deutschland?
- Wie viele Kilogramm Menschenkot entstehen in unserer Stadt an einem Tag? Wie viel in ganz Deutschland?
- Wie viel Müll produzieren die Deutschen in einem Jahr? Welches Volumen nimmt der Müll ein? Passt er in die Allianz-Arena?
- Wie viel Müll produzieren alle Schüler der Schüler zusammen? Passt er in die Schule?
- Wer produziert mehr CO2 - Die Menschen der BRD mit dem CO2 beim Ausatmen ihrer Atemluft oder die Kraftfahrzeuge Deutschlands? *(Modellrechnung siehe unten)
- Wie viel CO2 ( ➜ Kohlenstoffdioxid) atmet ein Mensch im Verlauf seines Lebens aus?
Lösungsansatz siehe unten
Längen
- Könnten alle Menschen von Deutschland eine Kette rund um Deutschland bilden? (Grenzlänge etwa 3757 km)
- Um wie viele cm wachsen die Haare auf deinem Kopf im Jahr? Wie lang würde es dauern, bis sie so lang wie bei Rapunzel wären?
- Wenn alle Menschen in der vollbesetzten Allianz-Arena sich an der Hand fassen und eine Menschenkette bilden - ginge die Schlange bis nach Augsburg oder Nürnberg?
- Wenn der Schnee nicht tauen würde - wie hoch läge er nach 10 Jahren in unserem Schulhof?
- Wenn eine Ameise proportional dieselb Wegstrecke wie ein Schüler pro Tag zurücklegt - wie viele Meter ist sie gelaufen?
- Wenn sich alle Kinder der Klasse /der Schule an der Hand fassen - reicht die Schlange um das Schulgebäude / den Sportplatz? (Armspanne messen)
- Beim Lotto 6 aus 49 beträgt die Wahrscheinlichkeit 1:139.868.160. Wenn du 139.868.160 Ein-Euro-Stücke aufeinander stapelst, wie hoch wäre der Turm?
- Wie groß ist die Blattberfläche eines Nadelbaums im Vergleich zu einem Laubbaum?
- Wie hoch wäre ein Stapel, wenn man diesen mit 5 €-Scheinen aus dem Lottojackpot dieser Woche stapeln würde?
- Wie lang ist die ganze Zahnpasta aus einer Tube?
- Wie lang sind alle deine Haare zusammen? Reicht es quer durch Deutschland?
- Wie lang ist der Wollfaden eines Strickpullovers?
- Wie lang wäre eine 1 Meter hohe Mauer aus den Plastikflaschen, die an eurer Schule im Verlauf von 9 Schülerjahren getrunken werden?
- Wie lange würdest du brauchen, um von Kiel nach Konstanz zu laufen?
- Wie viele Autos stehen in einem 100 km langen Stau?
- Wie viele Kilometer legt ein Schüler in einem Schuljahr während des Sportunterrichts zurück?
- Wie viele Kilometer legt ein Schüler in seinem Schülerleben auf dem Weg zur Pause zurück?
- Wie viele Kilometer legt ein Storch in seinem Leben zurück?
- Wie viele Meter hast du deinen Füller über das Papier bewegt, wenn du einen Aufsatz schreibst?
- Wie viele Meter Spaghetti isst du bei einer Mahlzeit? Im Jahr? Im Leben? Reicht die Länge zum Mond?
- Wie viele Meter wachsen deine Fingernägel in deinem Leben?
- Wie viele Meter "Wurst" legt ein Hund in seinem Hundeleben beim Gassi-Gehen ab?
- Wie viele Meter schaukelst du in 5 Minuten - Wie lange brauchst du für einen Kilometer??
- Wie viele Umdrehungen macht ein Autoreifen bei einem Ausflug nach Berlin?
Gewicht
- Wenn man einen Aufzug zur Weltraumstation ISS bauen würde, die in 400 km Höhe die Erde umkreist - wie schwer wäre dieser Aufzug, wenn er wie der Stuttgarter Fernsehturm gebaut wäre?
- Der Aufzug im Fernsehturm Stuttgart benötigt 36 Sekunden für eine Fahrt nach oben. Wie lange dauert dann die Fahrt zur ISS?
- Der derzeitige amerikanische Präsident wünscht sich eine Mauer zwischen Amerika und Mexiko. Diese soll mindestens 3 Meter hoch sein. Wie viel Beton (Stahl/Ziegelsteine) wird benötigt
- Wenn in der Ortsdurchfahrt alle 4 Minuten ein 30-Tonnen-LKW an dir vorbeidonnert - wie viele Walfische wären das von 7 Uhr morgens bis 19 Uhr abends?
- Wenn alle SchülerInnen deiner Schule auf einer Riesenwippe säßen, wie lang müsste für das Gleichgewicht dann die andere Seite sein, wenn dort das Lehrerkollegium sitzt?
- Wie schwer sind alle Schüler der Schule zusammen?
- Wie viel wiegen die Computer, die in Deutschland im Jahr auf dem Schrott landen?
- Wie viel wiegt der Müll, den die Deutschen im Jahr wegwerfen?
- Wie viel wiegt die Zugspitze?
- Wie viele Bodenseefähren wiegen so viel wie das Wasser im Bodensee?
- Wie viele Gummibärchen wiegen so viel wie ein Braunbär?
- Wie viele Kilogramm isst du im Jahr? Hast du in deinem Leben bereits das Gewicht eines Elefanten gevespert?
Flächen
- An einer Supermarktkasse wird im Schnitt alle 5 Minuten ein Kunde abkassiert. Welche Fläche könnte man mit den Einnahmen in Form von 10 €-Scheinen auslegen?
- Könnte man mit den Fotokopien, die an der Schule in einem Jahr hergestellt werden, alle Klassenräume der Schule tapezieren?
- Nach dem Golfkrieg wurden in der Wüste die Minen dadurch zerstört, dass Bulldozer den Sand wie Schnee vor sich hergeschoben haben und die Minen zur Explosion brachten. Wie lange benötigt ein Bulldozer für eine Fläche von 10 km²
- Passen alle Schüler der Schule in ein Klassenzimmer?
- Welche Fläche Deutschlands wird mit Autos überdeckt?
- Wenn alle Menschen der Erde ganz dicht nebeneinander stehen würden - wie viel Platz bräuchte man für die gesamte Erdbevölkerung? Wäre die Fläche von Europa, Deutschland oder Hamburg groß genug?
- Wenn die bewohnbare Erdoberfläche gleichmäßig an alle Erdbewohner aufgeteilt würde - wie groß wäre dein Anteil?
- Wie groß ist die Oberfläche deiner Haut?
Ist die Hautoberfläche aller Schüler in der Klasse größer als die Oberfläche deines Klassenraumes ? - Wie groß ist die Fensterfläche deiner Stadt
- Wie groß ist die Schaufensterfläche der Einkaufsstraße
- Wie oft passt die Hautoberfläche der Nationalmannschaft auf ein Fußballfeld?
- Wie viele Verkehrsschilder stehen in deiner Stadt? Wie viele Fußballfelder könnte man mit den Verkehrsschildern deiner Stadt abdecken?
- Wie lange würde es dauern, den Schulhof komplett mit gekautem Kaugummi zu bedecken?
- Wie viele Quadratmeter Blech haben alle Verkehrsschilder deiner Stadt? In Deutschland?
- Wie viele Quadratmeter Hefte-Papier verbraucht ein Schüler in seiner Schulzeit? Wie viele Fußballstadions könnte man damit belegen?
- Wie viele Quadratmeter Pizza werden an einem Abend in einer Pizzeria verspeist?
- Wie viele Tafeln Schokolade braucht man um das Fußballfeld / denSchulhof auszulegen?
- Wie viele Zahnstocher passen auf ein Blatt Papier?
Geld
- Wenn dein gesamter Lebensverdienst als Stundenlohn ausbezahlt würde, wie viel ist eine deiner Lebensstunden wert?
- Wenn du eine Million im Lotto gewinnst - welchen Stundenlohn hättest du ab heute für den Rest deines Lebens?
- Der deutsche Staat hat knapp 2 Billionen Euro Schulden. Wie viele Koffer voller Geld (in 1000 Euro Scheinen) sind das? Wie hoch wäre ein Turm mit Ein-Euro-Münzen?
- Preise - gestern und heute. An einer alten Eisenbahnbrücke befindet sich eine Tafel, auf der die Baukosten 1909 mit 70.000 Mark angegeben werden.
War das billig? Wie hoch waren die Kosten der Eisenbahnbrücke im Vergleich zu den Lebenshaltungskosten?
Dazu kann man die Entwicklung des Brotpreises betrachten. 1909 kostete 1 kg Brot 0,50 Mark, heute im Schnitt (je nach Anbieter) 4 €. Somit lagen die Baukosten im Kaufkraft-Vergleich bei mindestens 560.000 € heutiger Währung.
Nimmt man als Vergleich die durchschnittlichen Monatslöhne, werden die Kosten realistischer. 1909 lag der durchschnittliche Monatslohn bei 89 Mark, 2020 bei etwa 3000 €, also ~33 Mal so hoch. Damit kommen wir auf realistische Baukosten von ~ 2,4 Mio.Euro.
was-war-wann.de-historische_werte-monatslohn
was-war-wann.de-historische_werte-brotpreise
was-war-wann.de-historische_werte-benzinpreise
Energie
- Wie viel Strom wird in eurer Stadt im Jahr für die Weihnachtsbeleuchtung verwendet?
- Wie viel Strom verbrauchen die Schüler deiner Schule mit dem Computer zu Hause im Jahr?
Benzin ist scheißteuer! Wirklich?
Da muss ich nun noch mal den Mathelehrer "raushängen" 😉
Benzinpreis 1961 - 0,58 DM = 0,27 € (Wechselkurs 2000)
durchschnittlicher Jahresverdienst - 2439 € Euro (umgerechnet von DM)
Benzinpreis heute: 1,70 €
durchschnittlicher Jahresverdienst 2021 - 24539 €
(~ Faktor 10)
Wäre der Benzinpreis im selben Verhältnis gestiegen, müsste heute der Liter Benzin 2,70 € kosten.
Daten von
Lohnentwicklung siehe de.statista-com-statistik-jahresarbeitslohn-in-deutschland-seit-1960
Benzinpreis was-war-wann.de-historische_werte-benzinpreise
Links zu Fermi-Aufgaben
➜ Abschnitt ansehen / wegblenden
Arbeitsblätter und Anweisungen
❱23Q4❱ ➜ texte-fermiaufgabe_auftraege.txtAufträge zur Lösung von Fermi-Aufgaben
Linktipps
❱21❱ ➜ archive-org: disk-mathematik-uni-halle-lehrerseite-fermi_fragen-pdfBeispiele für Fermi-Aufgaben und Lösungsansätze
❱21❱ ➜ halbtagsblog-de-tag-fermi
Sammlung von Fermi-Aufgaben
❱21❱ ➜ cspannagel-wordpress-com-liebesschloesser
Wie schwer sind die Liebesschlösser in Köln und mehr
❱24Q2❱ ➜ isb-bayern-de-Foerderschulen-Lernen-Individualisiertes_Lernen-13_fermiaufgabe-zip
Beispielbögen mit Aufgaben und (Schüler-)Lösungen für verschiedene Fermiaufgaben (Förderschulstufe)
❱21❱ ➜ physics-umd-edu-perg-fermi-fermi
University of Maryland Fermi Problems Site: wissenschaftliche Fermi-Aufgaben (engl.)
❱21❱ ➜ unterrichten-zum-de-wiki-Fermi-Aufgaben
Beispiele für Fermi-Aufgaben im ZUM-Wiki
Modellrechnung zur Atemluft-Aufgabe 1: Auto
➜ Abschnitt ansehen / wegblenden
Wer produziert mehr CO2 - Die Menschen der BRD mit dem CO2 beim Ausatmen ihrer Atemluft oder die Kraftfahrzeuge Deutschlands?
Mensch
In Ruhe liegt das Atemvolumen bei ungefähr 7,5 l/min, also 450 l /h, demnach 10800 l /d
(Nebeninfo: Ein Mensch atmet täglich etwa 20.000-mal und bewegt dabei rund zwölf Kubikmeter Luft.)
Die Ausatemluft enthält 78 % Stickstoff (N2), aber nur noch ca. 17 % Sauerstoff (O2) und ca. 4 % Kohlenstoffdioxid (CO2 ) sowie rund 1 % andere Bestandteile wie beispielsweise Aceton oder Wasserstoff
bei 4% CO2 sind das demnach täglich 10800*4/100 l = 432 l CO2 / Tag und Mensch
80.000.000 Menschen der BRD * 430 l/Tag = 34.400.000.000 = etwa 30 MRD Liter CO2 pro Tag ergeben * 365 =10.950 MRD Liter pro Jahr,
Ergebnis: Die Menschen der BRD produzieren durch die Atemluft etwa 10 Billionen Liter CO2 pro Jahr.
Auto
Mittlerer Ausstoß laut Industrie und Grenzwerten ca. 120 gr CO2 pro Kilometer.
Da CO2 die Molmasse 44u hat, besitzen 44g ein sogenanntes Molvolumen von 22,4 Liter bei 0 Grad
So entsprechen 120 gr ca. 60 Liter CO2 (bei 0°C, also eher mehr)
Gehen wir davon aus, dass ein Auto somit pro gefahrenem Kilometer im Mittel 60 Liter CO2 produziert.
Bei einer mittleren Jahresleistung von 15.000 Kilometer produziert ein Auto 15.000 * 60 = 900.000 Liter CO2 pro Jahr (die mittlere Jahresleistung habe ich aus meinem Erfahrungswert genommen. Sie könnte höher oder niedriger liegen.
10 Billionen / 900.000 = ca. 11 Millionen
Die Menschen der BRD produzieren also so viel CO2 wie 11 Millionen Autos pro Jahr.
Im Jahr 2018 gab es in der BRD 56 Mio zugelassene Fahrzeuge, davon 46,5 Mio PKW. (Quelle: https://de.statista.com/themen/1422/fahrzeugbestand/)
Anmerkungen
In Ruhe liegt das Atemvolumen bei ungefähr 7,5 l/min, also 450 l /h, demnach 10800 l /d
(Nebeninfo: Ein Mensch atmet täglich etwa 20.000-mal und bewegt dabei rund zwölf Kubikmeter Luft.)
Die Ausatemluft enthält 78 % Stickstoff (N2), aber nur noch ca. 17 % Sauerstoff (O2) und ca. 4 % Kohlenstoffdioxid (CO2 ) sowie rund 1 % andere Bestandteile wie beispielsweise Aceton oder Wasserstoff
bei 4% CO2 sind das demnach täglich 10800*4/100 l = 432 l CO2 / Tag und Mensch
80.000.000 Menschen der BRD * 430 l/Tag = 34.400.000.000 = etwa 30 MRD Liter CO2 pro Tag ergeben * 365 =10.950 MRD Liter pro Jahr,
Ergebnis: Die Menschen der BRD produzieren durch die Atemluft etwa 10 Billionen Liter CO2 pro Jahr.
Auto
Mittlerer Ausstoß laut Industrie und Grenzwerten ca. 120 gr CO2 pro Kilometer.
Da CO2 die Molmasse 44u hat, besitzen 44g ein sogenanntes Molvolumen von 22,4 Liter bei 0 Grad
So entsprechen 120 gr ca. 60 Liter CO2 (bei 0°C, also eher mehr)
Gehen wir davon aus, dass ein Auto somit pro gefahrenem Kilometer im Mittel 60 Liter CO2 produziert.
Bei einer mittleren Jahresleistung von 15.000 Kilometer produziert ein Auto 15.000 * 60 = 900.000 Liter CO2 pro Jahr (die mittlere Jahresleistung habe ich aus meinem Erfahrungswert genommen. Sie könnte höher oder niedriger liegen.
10 Billionen / 900.000 = ca. 11 Millionen
Die Menschen der BRD produzieren also so viel CO2 wie 11 Millionen Autos pro Jahr.
Im Jahr 2018 gab es in der BRD 56 Mio zugelassene Fahrzeuge, davon 46,5 Mio PKW. (Quelle: https://de.statista.com/themen/1422/fahrzeugbestand/)
Anmerkungen
- Weil die Atemluft "recyceltes CO2" ist, das wir aus unserem Energiehaushalt mit nachwachsenden Rohstoffen erzeugen, kann man das natürlich nicht mit dem CO2 gleichsetzen, das Fahrzeuge aus fossilen Energieträgern durch Verbrennung erzeugen. Das menschliche CO2 stammt aus dem aktuellen Kreislauf, PKW-CO2 fügt dem Kreislauf "altes, zuvor fossil gebundenes" CO2 hinzu.
- Schwarzer Humor: Würden wir die Menschen der BRD abschaffen, könnten mit dem eingesparten CO2 11 Millionen Autos autonom und klimaneutral fahren.
Modellrechnung zur Atemluft-Aufgabe 2: Bäume
➜ Abschnitt ansehen / wegblenden
Wie viel CO2 ( ➜ Kohlenstoffdioxid) atmet ein Mensch im Verlauf seines Lebens aus?
Zusatzaufgabe: Wie viele Bäume wachsen wegen der ➜ Atmung eines Menschen? Hinweis: Beim Ausatmen beträgt der Anteil im Schnitt 4% CO2
Zusatzaufgabe: Wie viele Bäume wachsen wegen der ➜ Atmung eines Menschen? Hinweis: Beim Ausatmen beträgt der Anteil im Schnitt 4% CO2
Das ➜ Atemzeitvolumen ist das Luftvolumen, das in einer bestimmten Zeitspanne eingeatmet und ausgeatmet wird. Es wird in l/min gemessen und definiert sich als Atmungsfrequenz multipliziert mit dem Atemzugvolumen. In Ruhe liegt es bei ungefähr 7,5 l/min.Der Atemgrenzwert (auch Minutengrenzwert) ist das bei maximalem Atemzugvolumen und maximaler Frequenz pro Minute ventilierbare Atemluftvolumen. Der Atemgrenzwert beträgt in der Regel 120 bis 170 Liter pro Minute.
Der Einfachheit halber gehe ich von einem Lebens-Mittelwert von 10 l/min aus. Das sind 600 l/h und somit 600×24×365×75 l in 75 Jahren = 394.200.000 l bzw. 394.200 m³. 4% dieser ausgeatmeten Luft sind CO2 - also 15768 m³. Das spezifische Gewicht von CO2 beträgt 1,98 kg·m−3. 15768 m³ entstsprechen somit 31220 kg oder ca. 31 Tonnen.
Wie viel CO2eines Menschen nimmt demnach ein Baum eigentlich auf?
Wichtig zu wissen ist dazu die Info zur ➜ CO2-Aufnahme von Bäumen
Daraus: Eine 120-jährige Buche hat ein Trockengewicht von 1,9 Tonnen, also rund 0,95 Tonnen Kohlenstoff. Dies multipliziert mit 3,67 ergibt 3,5 Tonnen CO2.
In 75 Jahren speichert die Buche 75/120stel von 3,5 t, also etwa 2,2 t
Damit ergibt sich, dass ein Mensch mit seiner Atemluft in seiner Lebensspanne von 75 Jahren 31/2,2 = 14 Buchen wachsen lässt.
Ohne den CO2 - Ausstoß von Auto, Heizung, Flugreisen ...
Wenn nun jeder Mensch 20 Buchen (oder andere, seiner Umgebung angepasste Bäume) pflanzt, könnte er/sie halbwegs klimaneutral existieren - sofern die Bäume eine mindestens doppelt so lange Lebensspanne haben. Denn die Berechnungen basieren auf "ausgewachsenen Bäumen".
Wie viele Menschen passen in den Bodensee?
➜ Abschnitt ansehen / wegblenden
Zur "Migrantenschwemme" und der Behauptung, das Boot sei voll:
Geht man für die folgende Rechnung modellhaft davon aus, dass ein Mensch im Durchschnitt (Baby-Opa) ca. 50 kg wiegt und dass er in der Hauptsache aus Wasser besteht, sein spezifisches Gewicht also 1,0 sei - dann nimmt ein Mensch im Schnitt ein Volumen von 50 Liter ein.
Bei einer Erdbevölkerung von derzeit ca. 8 Milliarden Menschen hat die Menschheit demnach ein Gesamtvolumen von 400 Milliarden Liter.
Dies sind umgerechnet 400 Millionen Kubikmeter oder 0,4 Kubikkilometer.
Der Bodensee hat ein Volumen von 48 Kubikkilometer. siehe ➜ de-wikipedia-org-Bodensee
Demnach würde die gesamte Menschheit in flüssigem Zustand 120 mal in den Bodensee passen.
Berechnet mit Potenzen - genauso morbide ;-)
Der Bodensee ist nicht nur groß, sondern auch sehr tief.
Deshalb passen 48 Kubik-Kilometer Wasser rein. Das sind 48.000.000.000 m³ oder 48×10¹² Liter.
Ein Mensch wiegt im Durchschnitt (von Baby bis Greis - und weil es sich leichter rechnen lässt) 50 Kilo. Das entspricht 50 Liter Wasser.
Die Menschheit mit 8 Milliarden Menschen entspricht so 400 Milliarden Litern - wenn man alle als Flüssigkeit betrachtet. Das sind 4×10¹¹ Liter.
Die gesamte Menschheit könnte somit in flüssigem Zustand 48×10¹² geteilt durch 4×10¹¹ = 120 Mal im See versenkt werden.
Das ist eine nette Vorstellung, die allen widerspricht, die behaupten, dass im Paradies kein Platz für die Menschheit sei - zumal sich dort sowieso nur der Astralleib und die Seele befinden, die ein viel geringeres Volumen einnehmen.
Die Rechnung taucht weiter oben bei den Zehnerpotenzen nochmal auf: Menschen im Bodensee - dort habe ich die Ausrechnung mit 10-er-Potenzen abgelegt
So viel zur Selbstüberheblichkeit und zum Anthropozentrismus.
8 Milliarden Menschen ergeben (mit 50 Liter Durchschnittsvolumen gerechnet) 4×10¹¹ Liter = 4×10¹¹ dm³.
Die Frage lautet demnach mathematisch: Welche Resthöhe bleiben den 4×10¹¹ dm³-Würfelchen, wenn ich sie gleichmäßig über die Oberfläche des Sees verteile.
Die Oberfläche des Bodensees beträgt 536 km²= 536.000.000 m² = 53.600.000.000 dm² = 5,36 x 10¹⁰ dm²
Ich verteile 4x10¹¹ dm³ = 40x10¹⁰ dm³ auf 5,36x10¹⁰ dm² Der Quotient ergibt ~ 7,46 dm ~ 75 cm.
Der Pegel würde um etwa 75 cm steigen. Allerdings nur, wenn alle gleichzeitig die Luft anhalten und den Kopf unter die Oberfläche tauchen. Nicht eingerechnet sind zudem das Luftvolumen der Lunge sowie eventuelle Flatulenzen in den Gedärmen.
Weitere Einschränkung: Damit die Rechnung stimmt, müsste um den gesamten See herum eine Mauer gebaut werden. Weil die Uferböschung jedoch flach ist, würde die Oberfläche um einiges größer - und der Pegel würde nur wenige Zentimeter steigen. Keiner der Orte am Bodensee hätte ein Problem mit dem Pegel - weil 75 cm Sicherheitsmarge sowieso überall bestehen.
Bei einer Erdbevölkerung von derzeit ca. 8 Milliarden Menschen hat die Menschheit (wie oben gezeigt) ein Gesamtvolumen von 400 Milliarden Liter im Äquivalent von Wasser, daher ein Gewicht von 400 Milliarden Kilogramm = 400 Millionen Tonnen.
Ein Flugzeugträger der Nimitz-Klasse hat eine Verdrängung von ~ 100.000 Tonnen. Das Gewicht der Menschheit entspricht somit 4000 Flugzeugträgern - und würde den Meeresspiegel nur unwesentlich ansteigen lassen.
400 Millionen Tonnen klingen bombastisch. Die Erde hat eine Masse von knapp 6 Trilliarden Tonnen. Die Masse der Menschen wäre somit ein fünfzehn Billionstel der Erdmasse - momit der Faktor angegeben ist, die Einfluss auf die Umlaufbahn hätte
Ein 70 Kilogramm wiegender Mann besteht aus etwa 3*1013 Körperzellen - also rund 30 Billionen.
Somit entspricht die gesamte Menschheit im Vergleich zur Erdmasse ziemlich genau 2 Körperzellen ;-)
❱22Q4❱ ➜ https://www.spektrum.de/kolumne/doomsday-in-spaetestens-17-000-jahren-droht-der-weltuntergang/2069442
Untergang der Menschheit in 17.000 Jahren
Die Menschheit mit 8 Milliarden Menschen entspricht ca. 400 Milliarden Litern, wenn man mit 50 kg bzw. Liter pro Person im Schnitt rechnet und die Menschheit als Flüssigkeit betrachtet. Das sind 4×10¹¹ Liter
In weniger als 3 Jahren ist demnach die gesamte Menschheit in Form von Bier "weggesoffen"
Rechenweg 1
Geht man für die folgende Rechnung modellhaft davon aus, dass ein Mensch im Durchschnitt (Baby-Opa) ca. 50 kg wiegt und dass er in der Hauptsache aus Wasser besteht, sein spezifisches Gewicht also 1,0 sei - dann nimmt ein Mensch im Schnitt ein Volumen von 50 Liter ein.
Bei einer Erdbevölkerung von derzeit ca. 8 Milliarden Menschen hat die Menschheit demnach ein Gesamtvolumen von 400 Milliarden Liter.
Dies sind umgerechnet 400 Millionen Kubikmeter oder 0,4 Kubikkilometer.
Der Bodensee hat ein Volumen von 48 Kubikkilometer. siehe ➜ de-wikipedia-org-Bodensee
Demnach würde die gesamte Menschheit in flüssigem Zustand 120 mal in den Bodensee passen.
Rechenweg 2
Berechnet mit Potenzen - genauso morbide ;-)
Der Bodensee ist nicht nur groß, sondern auch sehr tief.
Deshalb passen 48 Kubik-Kilometer Wasser rein. Das sind 48.000.000.000 m³ oder 48×10¹² Liter.
Ein Mensch wiegt im Durchschnitt (von Baby bis Greis - und weil es sich leichter rechnen lässt) 50 Kilo. Das entspricht 50 Liter Wasser.
Die Menschheit mit 8 Milliarden Menschen entspricht so 400 Milliarden Litern - wenn man alle als Flüssigkeit betrachtet. Das sind 4×10¹¹ Liter.
Die gesamte Menschheit könnte somit in flüssigem Zustand 48×10¹² geteilt durch 4×10¹¹ = 120 Mal im See versenkt werden.
Quintessenz
Das ist eine nette Vorstellung, die allen widerspricht, die behaupten, dass im Paradies kein Platz für die Menschheit sei - zumal sich dort sowieso nur der Astralleib und die Seele befinden, die ein viel geringeres Volumen einnehmen.
Die Rechnung taucht weiter oben bei den Zehnerpotenzen nochmal auf: Menschen im Bodensee - dort habe ich die Ausrechnung mit 10-er-Potenzen abgelegt
So viel zur Selbstüberheblichkeit und zum Anthropozentrismus.
Badewannen-Pegel
Erweiterte Frage: Um wie viel steigt der Pegel des Bodensees, wenn alle Erdenbewohner (8 Mrd) gleichzeitig im See “baden” gehen?8 Milliarden Menschen ergeben (mit 50 Liter Durchschnittsvolumen gerechnet) 4×10¹¹ Liter = 4×10¹¹ dm³.
Die Frage lautet demnach mathematisch: Welche Resthöhe bleiben den 4×10¹¹ dm³-Würfelchen, wenn ich sie gleichmäßig über die Oberfläche des Sees verteile.
Die Oberfläche des Bodensees beträgt 536 km²= 536.000.000 m² = 53.600.000.000 dm² = 5,36 x 10¹⁰ dm²
Ich verteile 4x10¹¹ dm³ = 40x10¹⁰ dm³ auf 5,36x10¹⁰ dm² Der Quotient ergibt ~ 7,46 dm ~ 75 cm.
Der Pegel würde um etwa 75 cm steigen. Allerdings nur, wenn alle gleichzeitig die Luft anhalten und den Kopf unter die Oberfläche tauchen. Nicht eingerechnet sind zudem das Luftvolumen der Lunge sowie eventuelle Flatulenzen in den Gedärmen.
Weitere Einschränkung: Damit die Rechnung stimmt, müsste um den gesamten See herum eine Mauer gebaut werden. Weil die Uferböschung jedoch flach ist, würde die Oberfläche um einiges größer - und der Pegel würde nur wenige Zentimeter steigen. Keiner der Orte am Bodensee hätte ein Problem mit dem Pegel - weil 75 cm Sicherheitsmarge sowieso überall bestehen.
Nebenrechnung zum Gesamtgewicht
Mit den oben angegebenen Zahlen kann man auch leicht das Gewicht der Menschheit berechnen:Bei einer Erdbevölkerung von derzeit ca. 8 Milliarden Menschen hat die Menschheit (wie oben gezeigt) ein Gesamtvolumen von 400 Milliarden Liter im Äquivalent von Wasser, daher ein Gewicht von 400 Milliarden Kilogramm = 400 Millionen Tonnen.
Ein Flugzeugträger der Nimitz-Klasse hat eine Verdrängung von ~ 100.000 Tonnen. Das Gewicht der Menschheit entspricht somit 4000 Flugzeugträgern - und würde den Meeresspiegel nur unwesentlich ansteigen lassen.
Nebenrechnung für Physiker
Würde die Erdbahn beeinflusst, wenn alle Menschen der Erde sich in Berlin versammeln und gleichzeitig im Takt hüpfen?400 Millionen Tonnen klingen bombastisch. Die Erde hat eine Masse von knapp 6 Trilliarden Tonnen. Die Masse der Menschen wäre somit ein fünfzehn Billionstel der Erdmasse - momit der Faktor angegeben ist, die Einfluss auf die Umlaufbahn hätte
Nebenrechnung für Biologen
Welcher Körperteil eines Menschen wiegt ein fünfzehn Billionstel der Körpermasse?Ein 70 Kilogramm wiegender Mann besteht aus etwa 3*1013 Körperzellen - also rund 30 Billionen.
Somit entspricht die gesamte Menschheit im Vergleich zur Erdmasse ziemlich genau 2 Körperzellen ;-)
Anmerkung
Derzeit leben ca. 8 Milliarden Menschen auf der Erde. Der Grund dafür liegt nicht in der Geburtenrate, sondern in der Überlebenswahrscheinlichkeit. Wer in der Steinzeit 30 Jahre alt wurde, war Methusalem. In den Industrienationen liegt die durchschnittliche Lebenserwartung heute über 80 Jahre. 117 Milliarden Menschen lebten bislang auf der Erde. Sagt die Mathematik. Und die irrt sich NIEMALS!❱22Q4❱ ➜ https://www.spektrum.de/kolumne/doomsday-in-spaetestens-17-000-jahren-droht-der-weltuntergang/2069442
Untergang der Menschheit in 17.000 Jahren
Variante: Wenn die Menschheit eingeäschert würde - welches Volumen bliebe übrig?
- Annahme 1: Im Mittelwert (von Baby bis Greis) wiegt ein Mensch 50 kg
- Annahme 2: Ein Mensch besteht zu 60-90% aus Wasser. Rechnen wir also mit 25% "Trockenmasse"
- Annahme 3: Somit hat ein Mensch im Welt-Durchschnitt ein Trockengewicht von 12,5 kg, bzw. ein "entwässertes Volumen von 12,5 Litern
- Derzeit leben knapp 8 Mrd Menschen auf der Erde. Diese haben somit ein Gesamtvolumen von 12,5 * 109 Litern.
- Das entspricht ca. einem Würfel mit 12,5 * 106 m3
- Die Kaaba in Mekka ist 13,10 m hoch und hat eine Grundfläche von 11,03 m × 12,62 m, besitzt also ~ ein Volumen von ~ 1800 m3
- Die Menschheit könnte somit in knapp 7000 Urnen mit der Größe der Kaaba abgefüllt werden.
Menschheit vs. Bierkonsum
Die Weltproduktion an Bier betrug im Jahr 2018 etwa 1,429 Milliarden Hektoliter Bier, das sind ~1,43 * 1011 Liter.Die Menschheit mit 8 Milliarden Menschen entspricht ca. 400 Milliarden Litern, wenn man mit 50 kg bzw. Liter pro Person im Schnitt rechnet und die Menschheit als Flüssigkeit betrachtet. Das sind 4×10¹¹ Liter
In weniger als 3 Jahren ist demnach die gesamte Menschheit in Form von Bier "weggesoffen"
Benzin am Alpenrand und Bodensee - eine ökonomisch-ökologische Rechnung
➜ Abschnitt ansehen / wegblenden
Eine Matheaufgabe für die "grenznahen KuK" als Beitrag zu ökologisch-ökonomischer Bildung
Lohnt sich die Fahrt zum Tanken nach Österreich?- Annahme 1: Der Sprit ist 20 ct billiger (in der Regel nicht - aber nehmen wir mal an...)
- Annahme 2 a) Im Tank befindet sich noch Sprit - und man musste sich nicht nach Österreich schleppen lassen.
- Annahme 2 b) Man kann daher 50 Liter nachfüllen.
Anmerkung: In Österreich dürfen im PKW maximal 10 Liter Benzin im Ersatzkanister transportiert werden. Derzeit hätte die Verkehrspolizei Österreichs vermutlich eine lukrative Bußgeld-Einnahmequelle und könnte die Tanks im Fuhrpark mit den beschlagnahmten Spritmengen günstigst füllen ;-) - Ergebnis: Man hat 10 € gespart.
Doch... Moment! Die Tanke ist 25 Kilometer entfernt. Man fährt also 50 Kilometer hin- und zurück.
- Annahme 3: Der fahrbare Untersatz ist sparsam und schluckt 7 Liter/100 Kilometer (bei dieser "Kurzstrecke" und im Winter - mit Berg- und Tal im Allgäu eher mehr, aber lassen wir's mal so stehen)
- Ergebnis 1: Zur Tanke wurden 3,5 Liter verbraucht. Heute für 1,499 €, macht 5,25 € Spritverbrauch.
- Ergebnis 2: Man hat also nur 4,75 € gespart.
Heute gab es Stau an der Tanke und auf der Autobahn. Für 50 Kilometer kann man eh' im Schnitt 1 Stunde Fahrzeit rechnen.
Macht einen Stundenlohn von 4,75 €.
Super! Ohne E10.
Rechnet man noch Abschreibung, Bremsen- und Reifenabnutzung sowie Wertverlust des Fahrzeuges usw. dazu - grob 20 ct pro Fahrkilometer, dann ..... könnt ihr euch das selbst ausrechnen.
Hatte ich erwähnt, dass die oben genannte Rechnung nur bis zu einer Distanz von 25 Kilometer gilt?
Sind wir eigentlich da?
➜ Abschnitt ansehen / wegblenden
Und um es auf die Spitze zu treiben:
Aus wie viel "Etwas" und wie viel "Nichts" besteht ein Mensch? Wie groß wären wir ohne das Nichts?
Ein Atom besteht zu 99,99999 % aus NICHTS als Zwischenraum zwischen den Protonen, Neutronen, Elektronen, Myonen usw.
(Vergleich: Wenn man sich ein Wasserstoffatom in der Größe des Kölner Doms vorstellt, ist der Kern so groß wie ein Tennisball und die Wände sind die Schale, auf denen das Elektron drumrumsaust - stimmt zwar als Modell wegen der Unschärferelation nicht, ist aber eine nette Größenvorstellung)
Auf der Seite 123mathe.de/physik-der-aufbau-der-atome steht dieser Vergleich:
"Die Erde hat einen Durchmesser von etwa 12.000 km=12.000.000 m. Zusammengepresst wäre sie eine Kugel von 120 m Durchmesser. "
Gehe ich von einem durchschnittlichen Volumen von 50 Litern pro Mensch aus, so bleiben (ohne Atomzwischenraum) 50 × 0,00001 = 0,0005 l komprimiertes Volumen übrig - gerade mal 0,5 cm3 = 0,5 ml. Ein knapper Teelöffel mit Protonen, Neutronen, Elektronen und weiterem Quarks. Die Masse bliebe jedoch gleich.
Wären unsere Augen nicht auf das sichtbare Licht mit einer Wellenlänge zwischen 320 nm und 750 nm (1 Nanometer=10⁻9 m) geeicht, das die Atome nicht durchdringen kann und daher reflektiert wird, sondern würden wir mit einer Wellenlänge "sehen", die kleiner ist als ein Elektronendurchmesser, der auf 3 fm (1 Femtometer= 10⁻15 m) geschätzt wird , könnten wir uns nicht sehen - weil diese Wellenlänge die Atome durchdringt.
Eigentlich sind wir durchsichtige Geisterwesen und (fast) nicht vorhanden (siehe auch das "Bodenseetheorem). Aber das war seit Wilhelm Conrad Röntgen eigentlich eh' klar.🤘
Aus wie viel "Etwas" und wie viel "Nichts" besteht ein Mensch? Wie groß wären wir ohne das Nichts?
Ein Atom besteht zu 99,99999 % aus NICHTS als Zwischenraum zwischen den Protonen, Neutronen, Elektronen, Myonen usw.
(Vergleich: Wenn man sich ein Wasserstoffatom in der Größe des Kölner Doms vorstellt, ist der Kern so groß wie ein Tennisball und die Wände sind die Schale, auf denen das Elektron drumrumsaust - stimmt zwar als Modell wegen der Unschärferelation nicht, ist aber eine nette Größenvorstellung)
Auf der Seite 123mathe.de/physik-der-aufbau-der-atome steht dieser Vergleich:
"Die Erde hat einen Durchmesser von etwa 12.000 km=12.000.000 m. Zusammengepresst wäre sie eine Kugel von 120 m Durchmesser. "
Gehe ich von einem durchschnittlichen Volumen von 50 Litern pro Mensch aus, so bleiben (ohne Atomzwischenraum) 50 × 0,00001 = 0,0005 l komprimiertes Volumen übrig - gerade mal 0,5 cm3 = 0,5 ml. Ein knapper Teelöffel mit Protonen, Neutronen, Elektronen und weiterem Quarks. Die Masse bliebe jedoch gleich.
Wären unsere Augen nicht auf das sichtbare Licht mit einer Wellenlänge zwischen 320 nm und 750 nm (1 Nanometer=10⁻9 m) geeicht, das die Atome nicht durchdringen kann und daher reflektiert wird, sondern würden wir mit einer Wellenlänge "sehen", die kleiner ist als ein Elektronendurchmesser, der auf 3 fm (1 Femtometer= 10⁻15 m) geschätzt wird , könnten wir uns nicht sehen - weil diese Wellenlänge die Atome durchdringt.
Eigentlich sind wir durchsichtige Geisterwesen und (fast) nicht vorhanden (siehe auch das "Bodenseetheorem). Aber das war seit Wilhelm Conrad Röntgen eigentlich eh' klar.🤘
Welches Volumen hat die Menschheit?
➜ Abschnitt ansehen / wegblenden
Schwarze Mathematik
Geht man davon aus, dass der Mensch zu etwa 65% aus Wasser besteht und dieses völlig verdunsten würde, sowie der Zwischenraum zwischen den Atomen herausgepresst würde - Welches Volumen haben die Protonen, Neutronen und Elektronen der Menschheit?Infos: de-wikipedia-org-wiki-K%C3%B6rperfl%C3%BCssigkeit
Auch ein Atom besteht hauptsächlich aus Zwischenraum.
"Die Erde hat einen Durchmesser von etwa 12.000 km. Zusammengepresst wäre sie eine Kugel von 120 m Durchmesser. "
Quelle: 123mathe.de/physik-der-aufbau-der-atome (Diese Aussage soll im Folgenden für die Berechnung verwendet werden)
Das Volumen reduziert sich dadurch nach folgender Rechnung:
Radius der Erde = 6000 km = 6.000.000 m
Volumen der Erde somit V=4/3 * π * r3 = 4/3 * π * 6.000.0003 = 4/3 * π * 6*1018 m3
Radius der Atomkugel = 60 m
Volumen der "gepressten" Erde somit V=4/3 * π * r3 = 4/3 * π * 603 = 4/3 * π * 6*104 m3
Setzt man beide Volumina ins Verhältnis, können 4/3 * π *6 gekürzt werden, der Verkleinerungsfaktor beträgt dann 104 / 1018 = 1/(10(14
Der Einfachheit halber gehe ich von 8 Mrd Menschen mit einem Durchschnittsvolumen von 50 Litern aus. (siehe Bodensee-Aufgabe)
Gesamtvolumen der Menschheit somit 400 Mrd Liter.
Abzügl. 65% Wasserverdunstung ergibt sich ein Volumen von 140 Mrd Litern = 1,4 * 1011 Liter
Abzügl. Zwischenraum der Atome ergibt dies 1,4 * 1011 / 1014 = 1,4 * 10-3 Liter = 1,4 cm-3
Mit der Kubikwurzel ergibt dies einen Gesamtmenschheitswürfel mit ca. 1,118 mm Kantenlänge - ohne H2O-Anteil.
Das Gesamtgewicht dieses Würfelchens reduziert sich jedoch nur um die verdunstete Wassermenge - wodurch das durchschnittliche spezifische Gewicht etwas mehr als 1,0 betragen würde. (Ich schätze es auf das Dreifache), also 3 kg pro dm3
Bei einem Gesamtvolumen (nach Wasserverdunstung und ohne Abzug des Atomzwischenraumes) von 140 Mrd Liter beträgt die Masse = 140 * 109 dm3 * 3 kg/dm3 = 4,2 * 1011 kg = 4,2 * 108 t = 420 Mio t
So viel wiegt dieses kleine Würfelchen Menschheit - ohne Zwischenraum. ;-)
Wie viel wiegt die mexikanische Grenze?
➜ Abschnitt ansehen / wegblenden
Fermi-Aufgaben können politisch sein.
Wie viel Prozent der Weltstahlproduktion würde eine Mauer zwischen den USA und Mexiko verbrauchen, wenn sie die Dimensionen auf dem Bild hat?
Grundinformation:
Die Grenze zwischen den Vereinigten Staaten und Mexiko ist 3144 Kilometer lang
Die Mauer ist ca. 9 m hoch (30-foot-tall=9.144 Meters). (siehe Abbildung) Auf dem Bild besteht sie aus diagonal gestellten Säulen aus ca 30 cm starken Platten. Diese stehen (aus der Abb. geschätzt) mit 20 cm Abstand.
Der erste Teil der Mauer bestand nur aus Röhren. Diese wurden wohl überklettert, sodass nun im oberen Bereich zusätzlich Stahlplatten angebracht werden. Diese haben (geschätzt eine Breite von 5m und 1,50m Höhe. Ich rechne mit einer minimalen Dicke von 0,5 cm, sodass jede Platte ein Volumen von 0,0375 m³ Stahl besitzt.
Für die folgende Modellrechnung gehe ich von 2 Säulen pro laufendem Meter und 1 Platte pro 5 Meter aus.
3144 km sind 3.144.000 m, es werden demnach 6.288.000 Quaderstelen für die Mauer (ohne Querstreben) benötigt.
Ein Säulenquader besitzt ein Volumen von 4 Platten * 9 m * 0,3 m * 0,005 m = 0,054 m³
Wie bereits errechnet, werden 6.288.000 Metallquader benötigt, was 6.288.000*0,054= 339.552 m³ Stahl enspricht.
Hinzu kommen für die Platten 3.144.000 m/5 = 628800 Platten mit je einem Volumen von 0,0375 m³ Stahl = 23580 m³ Stahl
Gesamtstahlbedarf: 363.132 m³
Bei einer Dichte von 7,9 g/cm3 oder kg/dm3 oder t/m³ wiegt die Mauer 363.132*7,9 t=2.868.742,8 t, also etwa 2,9 Mio Tonnen Stahl.
Knapp drei Millionen Tonnen Stahl für eine politische Idee sind schon eine Hausnummer.
Der Kampfpanzer Leopard II wiegt 62 t. Die Stahlmenge der Mauer entspricht dem Gewicht von knapp 48.387 Leopard-Panzern.
Insgesamt verfügen die Vereinigten Staaten über 29.920 gepanzerte Fahrzeuge - wobei die Abrahms-Panzer schwerer sind als die Leopard.
Gehen wir davon aus, dass Trump in Wirklichkeit das Motto "Schwerter zu Pflugscharen" SEHR genau nimmt und sämtliche Panzer der USA in Mauerstelen umschmelzen lässt.
Im Jahr 2017 wurden in den ➜ Vereinigten Staaten von Amerika rund 81,6 Millionen Tonnen Rohstahl erzeugt. Für die Mauer würden somit etwa 3,5 % der Jahresstahlproduktion der USA benötigt. Durchaus machbar.
Ein 5 Millimeter dickes und 1200-1500 Millimeter breites Stahlblech kostet in Deutschland, Frankreich und Benelux 499 Euro je Tonne per 14. Januar 2019
Die benötigten 2,9 Mio t schlagen daher mit 1.447.100.000 € "zu Buche". Nimmt man die Baukosten hinzu, könnten die von Trump angeforderten 5 Mrd Dollar tatsächlich knapp reichen.
Falls Trump alle Flugzeugträger der atomgetriebenen Nimitz-Klasse der USA für den Grenzzaun einschmelzen ließe, könnte er die Materialkosten senken. Da die Vereinigten Staaten jedoch nur 20 Flugzeugträger besitzen, müsste er noch zusätzlich einige Flugzeugträger der Chinesen und von Verbündeten einschmelzen lassen, um annähernd das Gesamtgewicht der benötigten 2,9 Mio Tonnen Stahl zu gewinnen.
Grundinformation:
Die Grenze zwischen den Vereinigten Staaten und Mexiko ist 3144 Kilometer lang
Die Mauer ist ca. 9 m hoch (30-foot-tall=9.144 Meters). (siehe Abbildung) Auf dem Bild besteht sie aus diagonal gestellten Säulen aus ca 30 cm starken Platten. Diese stehen (aus der Abb. geschätzt) mit 20 cm Abstand.
Der erste Teil der Mauer bestand nur aus Röhren. Diese wurden wohl überklettert, sodass nun im oberen Bereich zusätzlich Stahlplatten angebracht werden. Diese haben (geschätzt eine Breite von 5m und 1,50m Höhe. Ich rechne mit einer minimalen Dicke von 0,5 cm, sodass jede Platte ein Volumen von 0,0375 m³ Stahl besitzt.
Für die folgende Modellrechnung gehe ich von 2 Säulen pro laufendem Meter und 1 Platte pro 5 Meter aus.
3144 km sind 3.144.000 m, es werden demnach 6.288.000 Quaderstelen für die Mauer (ohne Querstreben) benötigt.
Ein Säulenquader besitzt ein Volumen von 4 Platten * 9 m * 0,3 m * 0,005 m = 0,054 m³
Wie bereits errechnet, werden 6.288.000 Metallquader benötigt, was 6.288.000*0,054= 339.552 m³ Stahl enspricht.
Hinzu kommen für die Platten 3.144.000 m/5 = 628800 Platten mit je einem Volumen von 0,0375 m³ Stahl = 23580 m³ Stahl
Gesamtstahlbedarf: 363.132 m³
Bei einer Dichte von 7,9 g/cm3 oder kg/dm3 oder t/m³ wiegt die Mauer 363.132*7,9 t=2.868.742,8 t, also etwa 2,9 Mio Tonnen Stahl.
Knapp drei Millionen Tonnen Stahl für eine politische Idee sind schon eine Hausnummer.
Der Kampfpanzer Leopard II wiegt 62 t. Die Stahlmenge der Mauer entspricht dem Gewicht von knapp 48.387 Leopard-Panzern.
Insgesamt verfügen die Vereinigten Staaten über 29.920 gepanzerte Fahrzeuge - wobei die Abrahms-Panzer schwerer sind als die Leopard.
Gehen wir davon aus, dass Trump in Wirklichkeit das Motto "Schwerter zu Pflugscharen" SEHR genau nimmt und sämtliche Panzer der USA in Mauerstelen umschmelzen lässt.
Im Jahr 2017 wurden in den ➜ Vereinigten Staaten von Amerika rund 81,6 Millionen Tonnen Rohstahl erzeugt. Für die Mauer würden somit etwa 3,5 % der Jahresstahlproduktion der USA benötigt. Durchaus machbar.
Ein 5 Millimeter dickes und 1200-1500 Millimeter breites Stahlblech kostet in Deutschland, Frankreich und Benelux 499 Euro je Tonne per 14. Januar 2019
Die benötigten 2,9 Mio t schlagen daher mit 1.447.100.000 € "zu Buche". Nimmt man die Baukosten hinzu, könnten die von Trump angeforderten 5 Mrd Dollar tatsächlich knapp reichen.
Falls Trump alle Flugzeugträger der atomgetriebenen Nimitz-Klasse der USA für den Grenzzaun einschmelzen ließe, könnte er die Materialkosten senken. Da die Vereinigten Staaten jedoch nur 20 Flugzeugträger besitzen, müsste er noch zusätzlich einige Flugzeugträger der Chinesen und von Verbündeten einschmelzen lassen, um annähernd das Gesamtgewicht der benötigten 2,9 Mio Tonnen Stahl zu gewinnen.
Wie viele Backsteine braucht man, um das Obertor von Isny wieder aufzubauen?
➜ Abschnitt ansehen / wegblenden
Die Stadt Isny im Allgäu ist noch heute in weiten Teilen von der mittelalterlichen Stadtmauer und verschiedenen Türmen umgeben. Im Jahr 1830 wurde das "Obertor" (auch "Lindauer Tor") abgerissen.
Heute ist die Innenstadt verkehrsberuhigte Zone und Fußgängerbereich. Das Tor wäre kein besonderes Hindernis.
2012 gab es Pläne (und Vorschläge) des Architekten Zumthor, das Obertor wieder aufzubauen - allerdings in einer modernen Zumthor-Variante aus Glasbausteinen. Per Bürgerentscheid wurde das damals abgelehnt.
Der Plan Zumthors hätte etwa eine halbe Million Glasbausteine benötigt.
Fermi-Aufgabe: Wie viele Backsteine im Reichsformat (RF) würden für den Aufbau der originalen Version benötigt?
Aus statischen Gründen hatten im Mittelalter die Fundamentmauern oft eine Mächtigkeit von 1 Meter und verjüngten sich nach oben.
in dieser Abbildung ist auch das Vortor und die seitliche Mauer zu sehen. Aus der Abbildung lassen sich die ungefähren Maße entnehmen. Anhaltspunkt: Die mittlere Stockwerkshöhe dürfte bei 2,50 Meter liegen.

Beispielrechnung Haupttor
Annahmen
Die Maße sind aus der Abbildung heraus geschätzt.
Durchschnittlicher Mauerquerschnitt 0,5 m (unten 1m, oben 0,25 m)
Breite des Turmes: ~ 5 m
Höhe des Turmes ~ 15 m (geschätzte Stockwerkshöhe 2m-2,50 m)
Aufsatz wird durch Tor ausgeglichen
Backstein im Reichsformat (RF) 24cm * 11,5cm * 6,3cm = 0,0017388 m3
Rechnung
Vaußen = 15*5*5 m3 = 375 m3
Vinnen = 15*4*4 m3 = 240 m3
VMauerwerk = 375-240 = 135 m3
Beispielrechnung Rundtürme
Grundlagen:
2 Türme
durchschnittlicher Mauerquerschnitt 0,5 m
Breite des Turmes: d ~ 4 m, raußen = 2 m, rinnen = 1,5 m
Höhe des Turmes h ~ 8,5 m
Rechnung
Vaußen = π*4*8,5 m3 = 107 m3
Vinnen = π*2,25*8,5 m3 = 60 m3
VMauerwerk = 107-60 = 47 m3
2 Türme haben somit ca. 90 m 3 Mauerwerk
Summe des gesamten Mauervolumens: 135+90 = 225 m3
Beispielrechnung Ziegelanzahl 225 m 3 / 0,0017388 m3 = 129.400 Stück
Ergebnis: Es würden überschlägig 130.000 Backsteine benötigt.
Isny hatte am 31.12.2023 gem. Wikipedia 15.190 Einwohner. Wenn jeder Bürger 8,6 Backsteine vorbeibringt, wäre das Material für den Wiederaufbau vorhanden. Rechnet man mit 150.000 Backsteinen, wären es für jeden Einwohner knapp 10 Stück. Das ist (auf zwei Mal) durchaus "tragbar" - ein Backstein im RF-Format wiegt 4,3 kg ;-)
2012 gab es Pläne (und Vorschläge) des Architekten Zumthor, das Obertor wieder aufzubauen - allerdings in einer modernen Zumthor-Variante aus Glasbausteinen. Per Bürgerentscheid wurde das damals abgelehnt.
Der Plan Zumthors hätte etwa eine halbe Million Glasbausteine benötigt.
Fermi-Aufgabe: Wie viele Backsteine im Reichsformat (RF) würden für den Aufbau der originalen Version benötigt?
Aus statischen Gründen hatten im Mittelalter die Fundamentmauern oft eine Mächtigkeit von 1 Meter und verjüngten sich nach oben.
in dieser Abbildung ist auch das Vortor und die seitliche Mauer zu sehen. Aus der Abbildung lassen sich die ungefähren Maße entnehmen. Anhaltspunkt: Die mittlere Stockwerkshöhe dürfte bei 2,50 Meter liegen.

Beispielrechnung Haupttor
Annahmen
Die Maße sind aus der Abbildung heraus geschätzt.
Durchschnittlicher Mauerquerschnitt 0,5 m (unten 1m, oben 0,25 m)
Breite des Turmes: ~ 5 m
Höhe des Turmes ~ 15 m (geschätzte Stockwerkshöhe 2m-2,50 m)
Aufsatz wird durch Tor ausgeglichen
Backstein im Reichsformat (RF) 24cm * 11,5cm * 6,3cm = 0,0017388 m3
Rechnung
Vaußen = 15*5*5 m3 = 375 m3
Vinnen = 15*4*4 m3 = 240 m3
VMauerwerk = 375-240 = 135 m3
Beispielrechnung Rundtürme
Grundlagen:
2 Türme
durchschnittlicher Mauerquerschnitt 0,5 m
Breite des Turmes: d ~ 4 m, raußen = 2 m, rinnen = 1,5 m
Höhe des Turmes h ~ 8,5 m
Rechnung
Vaußen = π*4*8,5 m3 = 107 m3
Vinnen = π*2,25*8,5 m3 = 60 m3
VMauerwerk = 107-60 = 47 m3
2 Türme haben somit ca. 90 m 3 Mauerwerk
Summe des gesamten Mauervolumens: 135+90 = 225 m3
Beispielrechnung Ziegelanzahl 225 m 3 / 0,0017388 m3 = 129.400 Stück
Ergebnis: Es würden überschlägig 130.000 Backsteine benötigt.
Isny hatte am 31.12.2023 gem. Wikipedia 15.190 Einwohner. Wenn jeder Bürger 8,6 Backsteine vorbeibringt, wäre das Material für den Wiederaufbau vorhanden. Rechnet man mit 150.000 Backsteinen, wären es für jeden Einwohner knapp 10 Stück. Das ist (auf zwei Mal) durchaus "tragbar" - ein Backstein im RF-Format wiegt 4,3 kg ;-)
Wer sind wir? Und wenn ja - wie viele?
Unter besonderer Berücksichtigung der Darmflora an einer Abzweigung zur Unsterblichkeit➜ Abschnitt ansehen / wegblenden
Die Antwort geben Physik und Chemie. Sie lautet: Ja. Wir sind unsterblich! Wir verschwinden nicht ins Nichts.
Das hat mit Energieerhaltung und dem Gesetz der Erhaltung der Masse zu tun. Bei chemischen Reaktionen geht kein Atom verloren.
Wir bestehen aus Atomen, die sich zu chemischen Verbindungen wie Molekülen gruppieren, die wiederum auf seltsame, geordnete Weise miteinander agieren und Organismen bilden - manchmal auch einen Menschen.
Ständig wandeln sich diese chemischen Verbindungen - die Nahrung, die wir aufnehmen, setzen wir um - einen Teil atmen wir als CO2 aus - das wiederum Teil eines Grashalmes oder Baumes wird. Einen Teil scheiden wir aus - die Atome werden als Dünger auf Felder ausgebracht, lassen Weizen wachsen, aus dem wiederum das Mehl für das Brötchen unseres Nachbarn wird. Somit werden wir Teil unseres Nachbarn, wenn er dieses Brötchen isst.
Weiter oben habe ich errechnet, dass ein Mensch im Laufe seines Lebens so viel CO2 ausatmet, dass es zur Bildung von 32 Buchen reicht. Leben wir in diesen Buchen fort? Der Kohlenstoff, den wir ausatmen war Teil unseres Organismus... bzw. Stoffwechsels, Teil des Specks am Bauch, den wir beim Abnehmen loswerden...
Sobald wir unter der Erde sind, werden wir Teil von Aber-Milliarden Kleinstlebewesen, Bakterien, Würmern usw - und unsere Atome "leben" in diesen weiter. Das ist der WIRKLICHE "Circle of life". Das hat jetzt nicht mehr viel mit Mathe zu tun. Wer mag, darf jedoch ausrechnen, wie viele Bakterien bei der Zersetzung einer Leiche satt werden. Davon abgesehen leben in unserem Darm mehr Bakterien als es Menschen auf der Erde gibt... Was der Frage: "Wer sind wir? Und wenn ja, wie viele?" eine unüberschaubare Zahl entgegensetzt.
Die ➜ Wikipedia beziffert die Zahl auf eine "Gesamtzahl von 10 bis 100 Billionen. Molekulare Analysen der 16S-ribosomalen DNA haben bisherige kulturabhängige Schätzungen von 200 bis 300 Arten auf bis zu 1800 Gattungen mit bis zu 36.000 Arten ansteigen lassen. Die zum Darmkanal gehörende Besiedlung eines Menschen enthält mindestens 500 bis 1000 unterschiedliche Arten (...) Im Darm befinden sich rund 1,3 mal so viel Mikroorganismen, wie der Organismus des Menschen Zellen enthält."
Schön. Auf diese Weise sind wir in alle Ewigkeit - und unsterblich - am Projekt "feed the world" beteiligt ;-)
Da bei einzelnen Reaktionen auch Energie freigesetzt wird, befindet sich immer auch ein Teil, der sich gestern noch in uns befand, heute als Wärmestrahlung im Weltraum.
Das hat mit Energieerhaltung und dem Gesetz der Erhaltung der Masse zu tun. Bei chemischen Reaktionen geht kein Atom verloren.
Wir bestehen aus Atomen, die sich zu chemischen Verbindungen wie Molekülen gruppieren, die wiederum auf seltsame, geordnete Weise miteinander agieren und Organismen bilden - manchmal auch einen Menschen.
Ständig wandeln sich diese chemischen Verbindungen - die Nahrung, die wir aufnehmen, setzen wir um - einen Teil atmen wir als CO2 aus - das wiederum Teil eines Grashalmes oder Baumes wird. Einen Teil scheiden wir aus - die Atome werden als Dünger auf Felder ausgebracht, lassen Weizen wachsen, aus dem wiederum das Mehl für das Brötchen unseres Nachbarn wird. Somit werden wir Teil unseres Nachbarn, wenn er dieses Brötchen isst.
Weiter oben habe ich errechnet, dass ein Mensch im Laufe seines Lebens so viel CO2 ausatmet, dass es zur Bildung von 32 Buchen reicht. Leben wir in diesen Buchen fort? Der Kohlenstoff, den wir ausatmen war Teil unseres Organismus... bzw. Stoffwechsels, Teil des Specks am Bauch, den wir beim Abnehmen loswerden...
Sobald wir unter der Erde sind, werden wir Teil von Aber-Milliarden Kleinstlebewesen, Bakterien, Würmern usw - und unsere Atome "leben" in diesen weiter. Das ist der WIRKLICHE "Circle of life". Das hat jetzt nicht mehr viel mit Mathe zu tun. Wer mag, darf jedoch ausrechnen, wie viele Bakterien bei der Zersetzung einer Leiche satt werden. Davon abgesehen leben in unserem Darm mehr Bakterien als es Menschen auf der Erde gibt... Was der Frage: "Wer sind wir? Und wenn ja, wie viele?" eine unüberschaubare Zahl entgegensetzt.
Die ➜ Wikipedia beziffert die Zahl auf eine "Gesamtzahl von 10 bis 100 Billionen. Molekulare Analysen der 16S-ribosomalen DNA haben bisherige kulturabhängige Schätzungen von 200 bis 300 Arten auf bis zu 1800 Gattungen mit bis zu 36.000 Arten ansteigen lassen. Die zum Darmkanal gehörende Besiedlung eines Menschen enthält mindestens 500 bis 1000 unterschiedliche Arten (...) Im Darm befinden sich rund 1,3 mal so viel Mikroorganismen, wie der Organismus des Menschen Zellen enthält."
Schön. Auf diese Weise sind wir in alle Ewigkeit - und unsterblich - am Projekt "feed the world" beteiligt ;-)
Da bei einzelnen Reaktionen auch Energie freigesetzt wird, befindet sich immer auch ein Teil, der sich gestern noch in uns befand, heute als Wärmestrahlung im Weltraum.
Die bucklige Verwandschaft - wie verwandt sind wir eigentlich?
Unter besonderer Berücksichtigung von Kaiser Karl dem Großen➜ Abschnitt ansehen / wegblenden
Wusstet ihr, dass fast alle Deutschen (und viele Franzosen) direkte Nachfahren von Karl dem Großen sind?
Über den vergangenen Zeitabschnitt der tausendzweihundertsechsundsechzig Jahre bis zum Jahr 2026 haben wir viele Vorfahren. In normalen Stammbäumen werden nur die männlichen Vorfahren erwähnt.
Nimmt man an, dass alle Nachkommen von Karl jeweils 2 zeugungsfähige Nachkommen mit wiederum 2 Kindern in die Welt gesetzt haben, die wiederum 2 zeugungsfähige Nachkommen zeugten, die... usw. ;-), dann geht das in Zweierpotenzen nach oben.
Wobei der Startwert anders gelegt werden müsste, immerhin hatte Karl 18 Kinder, 5 Ehefrauen und zahlreiche Geliebte.
Rechnet man pro Generation im Schnitt 28 Jahre, so sind seit Karls Zeugungsfähigkeit (742-814, also ca. 760) bis heute 1266 Jahre, folglich 45 Generationen durch.
Das ergibt 2⁴⁴ ~ 1,76×10¹³ Nachkommen ;-)
Anmerkung 1: Ja. Das sind mehr Menschen, als derzeit auf der Erde existieren. In den 1262 Jahren sind jedoch auch die meisten davon schon wieder gestorben, Kriegs- und Seuchenjahre haben die "bucklige Verwandschaft" zudem immer wieder massiv dezimiert ;-)
Anmerkung 2: Die Zahl dürfte viel zu hoch angesetzt sein,
weil
- innerhalb der Noblesse viel "Inzucht" herrschte und Cousins und Cousinen sich "freiten"
- auch die zu schwängernde Dienerschaft sich die Partner im Umkreis der Schlösser suchte und auf diese Weise im Verlauf von Generationen Inzucht betrieb 😉
Nun die Haupt- und Fermifrage: Wie viele Menschen der "Jetztzeit" sind in der BRD direkte Nachkommen von Karl?
Das Beispiel mit der 2-er-Potenz ist auch völlig hypothetisch und entspricht sicher nicht der Wirklichkeit. Das ist schon klar. Die Grundfrage lautet jedoch:
Wie wahrscheinlich ist es, dass ein Genschnipsel von Karl in dir oder mir existiert? ❱22Q2❱ ➜ focus-de-wissen-geschichte-eheleben-von-karl-dem-grossen-die-frauen-neben-dem-kaiser
Link zu den Nachfahren Karls des Großen
Anmerkung 1: Ja. Das sind mehr Menschen, als derzeit auf der Erde existieren. In den 1262 Jahren sind jedoch auch die meisten davon schon wieder gestorben, Kriegs- und Seuchenjahre haben die "bucklige Verwandschaft" zudem immer wieder massiv dezimiert ;-)
Anmerkung 2: Die Zahl dürfte viel zu hoch angesetzt sein,
weil
- innerhalb der Noblesse viel "Inzucht" herrschte und Cousins und Cousinen sich "freiten"
- auch die zu schwängernde Dienerschaft sich die Partner im Umkreis der Schlösser suchte und auf diese Weise im Verlauf von Generationen Inzucht betrieb 😉
Nun die Haupt- und Fermifrage: Wie viele Menschen der "Jetztzeit" sind in der BRD direkte Nachkommen von Karl?
Das Beispiel mit der 2-er-Potenz ist auch völlig hypothetisch und entspricht sicher nicht der Wirklichkeit. Das ist schon klar. Die Grundfrage lautet jedoch:
Wie wahrscheinlich ist es, dass ein Genschnipsel von Karl in dir oder mir existiert? ❱22Q2❱ ➜ focus-de-wissen-geschichte-eheleben-von-karl-dem-grossen-die-frauen-neben-dem-kaiser
Link zu den Nachfahren Karls des Großen
Lesestoff für Künstler*innen & Lichtbildner*innen
Neue und alte Techniken der Radierung und Edeldruckverfahren
Vom Hexenmehl und Drachenblut zur Fotopolymerschicht - ein Werkstattbuch
Tipps, Tricks, Anleitungen, Verfahren und Rezepturen aus 5 Jahrhunderten -
erlesen, erfahren, erfunden und gesammelt von Wolfgang Autenrieth
erlesen, erfahren, erfunden und gesammelt von Wolfgang Autenrieth
Nochmals erweiterte 7. Auflage, ISBN 978-3-9821765-0-5, zweispaltig im Großformat, 232 Seiten - 36,90 € zzgl. Versand
➥ Wege zum Buch
Zum Reinschnuppern: Das kostenlose ➜
"Alchemistische Online-Werkstattbuchversion" mit 180 Teilkapiteln








